hello algorithm chapter 3 / data structure types

思维导图

data structure types

逻辑结构

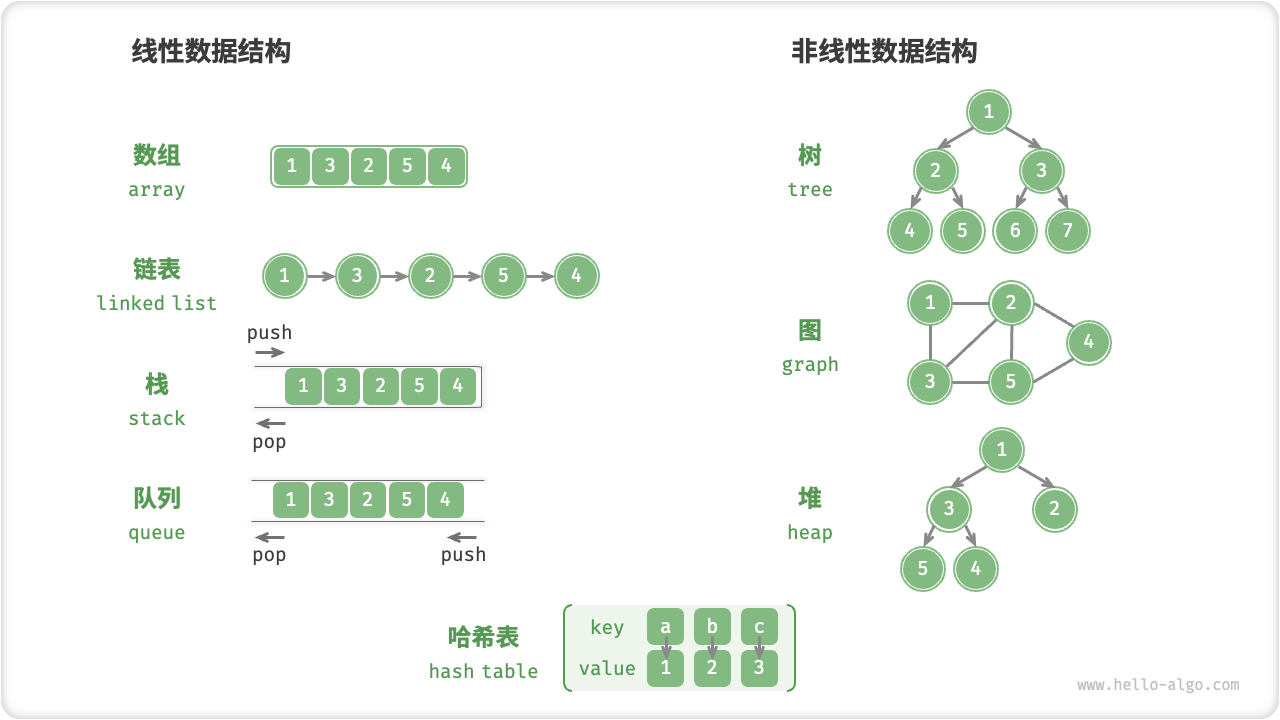
线性数据结构：数组、链表、栈、队列、哈希表。

非线性数据结构

网状结构：树、堆、哈希表，元素之间是一对多的关系。

树形结构：图，元素之间是多对多的关系。

物理结构

连续空间存储

静态数据结构，初始化之后长度不可变。底层数据结构：数组。

基于数组可实现：栈、队列、哈希表、树、堆、图、矩阵、张量（维度 ≥3 的数组）等。

分散空间存储

动态数据结构，初始化之后长度可变。底层数据结构：链表。

基于链表可实现：栈、队列、哈希表、树、堆、图等。

基本数据类型

基本数据类型以二进制的形式存储在计算机中

整数类型 byte、short、int、long

浮点类型 float、double

字符类型 char

布尔类型 boolean

数字编码

整数编码：

底层：原码、反码、补码。

计算机内部的硬件电路主要是基于加法运算。

解决零的歧义性

浮点数编码：

底层：将 32-bit 长度的二进制数分段拆分为符号位 S、指数位 E、分数位 N。

指数位 E = 0 和 E = 255 具有特殊含义，用于表示零、无穷大、NaN 等。

字符编码：

ASCII： 7 位二进制数（即一个字节的低 7 位）表示一个字符

GBK：ASCII 字符使用一个字节表示，汉字使用两个字节表示。

Unicode：Unicode 是一种字符集标准，而非一种字符集，本质上是给每个字符分配一个编号（称为 “码点”）。

UTF-8（8-bit Unicode Transformation Format）：对于长度为 1 字节的字符，将最高位设置为 0、其余 7 位设置为 Unicode 码点。对于长度为 n 字节的字符（其中 n > 1 ），将首个字节的高 n 位都设置为 1、第 n + 1 位设置为 0 ；从第二个字节开始，将每个字节的高 2 位都设置为 10 ；其余所有位用于填充字符的 Unicode 码点。

编程语言的字符编码：UTF-16（Java、C#、Python），UTF-8（Go、Rust），Unicode变长（Python）。

逻辑结构：线性与非线性

数据结构如同一副稳固而多样的框架。算法是运行在框架上逻辑。

线性结构比较直观，指数据在逻辑关系上呈线性排列；非线性结构则相反，数据无任何线性关系。

物理结构：连续与分散

在计算机中，内存和硬盘是两种主要的存储硬件设备。

硬盘：主要用于长期存储数据，容量较大（通常可达到 TB 级别）、速度较慢。
内存：用于运行程序时暂存数据，速度较快，但容量较小（通常为 GB 级别）。

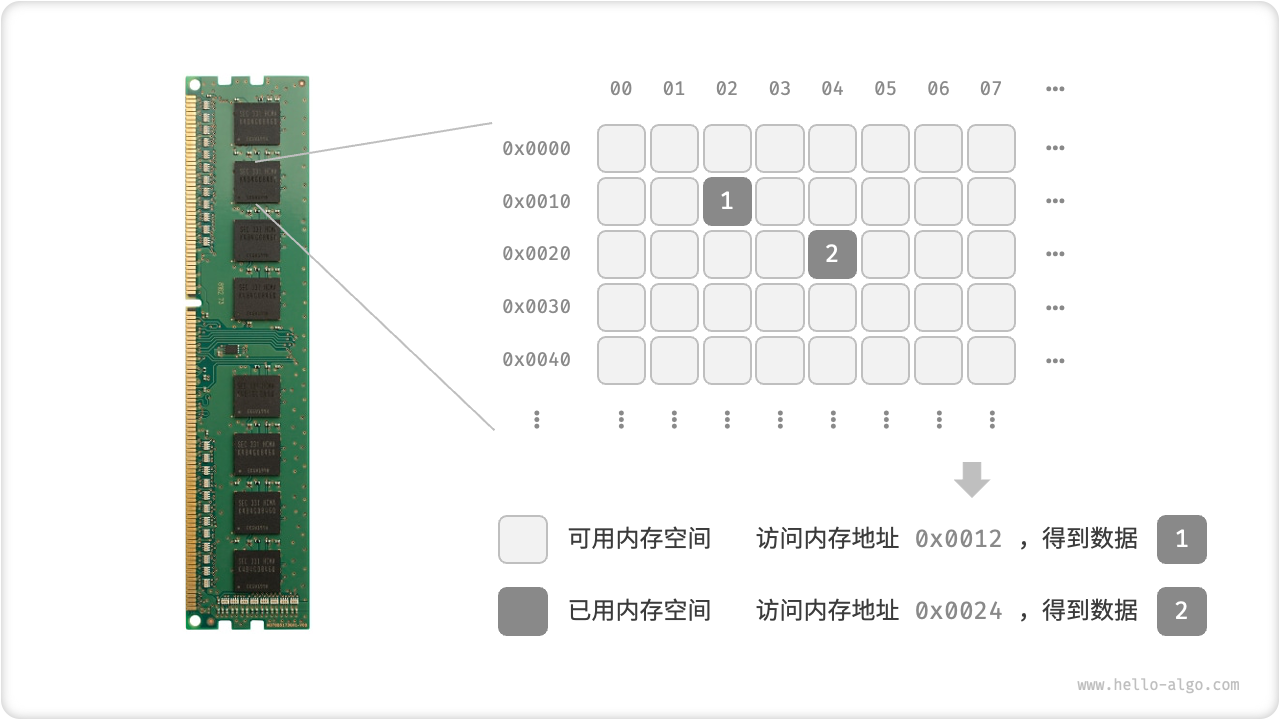
在算法运行过程中，相关数据都存储在内存中。图 3-2 展示了一个计算机内存条，其中每个黑色方块都包含一块内存空间。我们可以将内存想象成一个巨大的 Excel 表格，其中每个单元格都可以存储一定大小的数据，在算法运行时，所有数据都被存储在这些单元格中。

系统通过内存地址来访问目标位置的数据。如图 3-2 所示，计算机根据特定规则为表格中的每个单元格分配编号，确保每个内存空间都有唯一的内存地址。有了这些地址，程序便可以访问内存中的数据。

内存是所有程序的共享资源，当某块内存被某个程序占用时，则无法被其他程序同时使用了。因此在数据结构与算法的设计中，内存资源是一个重要的考虑因素。比如，算法所占用的内存峰值不应超过系统剩余空闲内存；如果缺少连续大块的内存空间，那么所选用的数据结构必须能够存储在分散的内存空间内。

物理结构反映了数据在计算机内存中的存储方式，可分为连续空间存储（数组）和分散空间存储（链表）。物理结构从底层决定了数据的访问、更新、增删等操作方法，同时在时间效率和空间效率方面呈现出互补的特点。

所有数据结构都是基于数组、链表或二者的组合实现的。例如，栈和队列既可以使用数组实现，也可以使用链表实现；而哈希表的实现可能同时包含数组和链表。

基于数组可实现：栈、队列、哈希表、树、堆、图、矩阵、张量（维度 ≥3 的数组）等。“静态数据结构”，这意味着此类数据结构在初始化后长度不可变。

基于链表可实现：栈、队列、哈希表、树、堆、图等。 “动态数据结构”，这类数据结构在初始化后，仍可以在程序运行过程中对其长度进行调整。

基本数据类型

基本数据类型是 CPU 可以直接进行运算的类型，在算法中直接被使用，主要包括以下几种类型。

整数类型 byte、short、int、long 。
浮点数类型 float、double ，用于表示小数。
字符类型 char ，用于表示各种语言的字母、标点符号、甚至表情符号等。
布尔类型 bool ，用于表示 “是” 与 “否” 判断。

基本数据类型以二进制的形式存储在计算机中。一个二进制位即为 1 比特。在绝大多数现代系统中，1 字节（byte）由 8 比特（bits）组成。

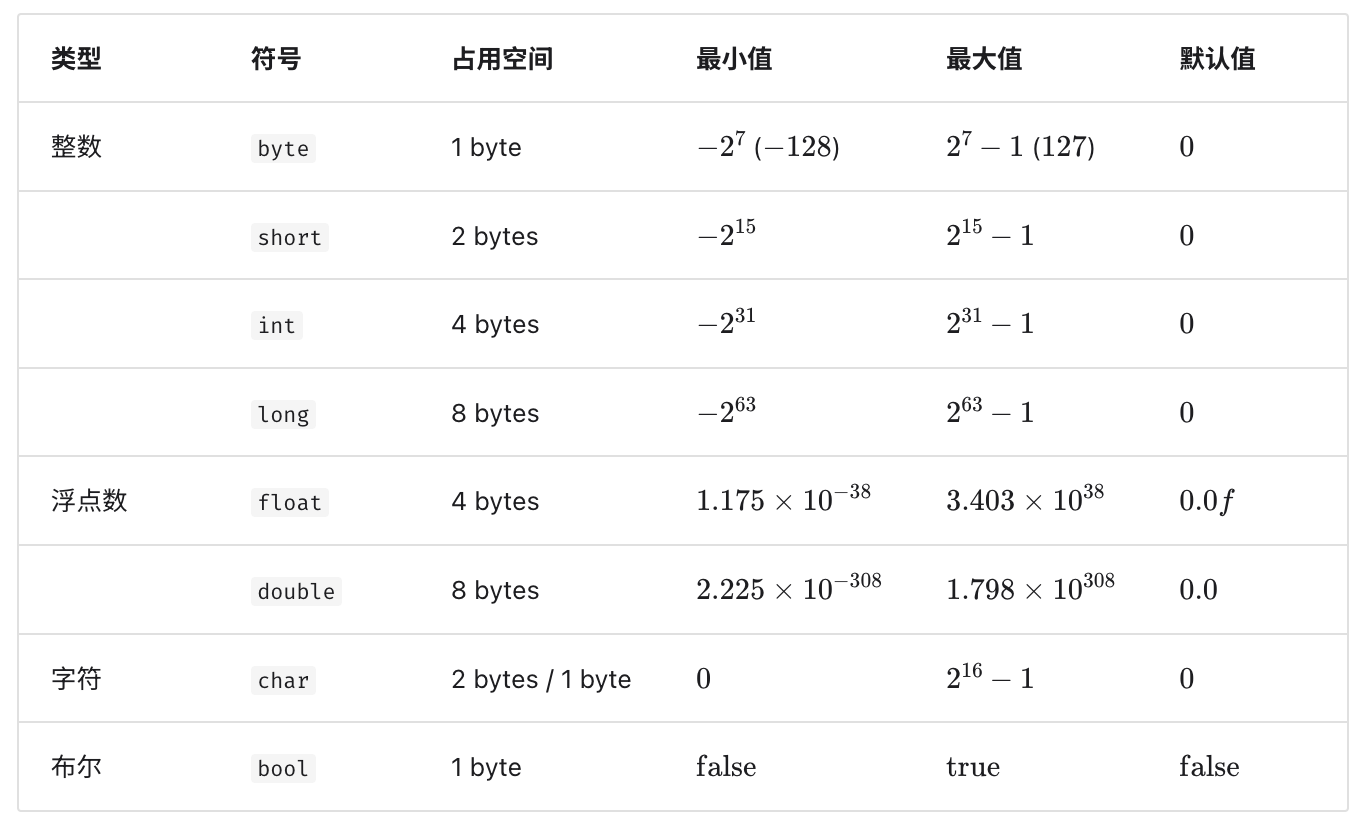
基本数据类型的取值范围取决于其占用的空间大小。下面以 Java 为例。

整数类型 byte 占用 1 byte = 8 bits ，可以表示 28 个数字。
整数类型 int 占用 4 bytes = 32 bits ，可以表示 232 个数字。

下图展示了各种基本数据类型的占用空间、取值范围和默认值。

数据结构是在计算机中组织与存储数据的方式。它的主语是 “结构” 而非 “数据”。

基本数据类型提供了数据的 “内容类型”，而数据结构提供了数据的 “组织方式”。

// 使用多种基本数据类型来初始化数组
int[] numbers = new int[5];
float[] decimals = new float[5];
char[] characters = new char[5];
boolean[] bools = new boolean[5];

数字编码

整数编码

首先，了解清楚什么是原码反码补码。

为什么不直接用原码？

原因一：原码无法直接加减

问题：在原码下计算 $1+(−2)$ ，得到的结果是 $−3$ ，这显然是不对的。

\[ 1 + (-2) \]

\[ -> 0000 0001(原码) + 1000 0010(原码) \]

\[ = 1000 0011 (原码 -3) \]

解决方案：引入反码。

为了解决此问题，计算机引入了「反码 1's complement code」。如果我们先将原码转换为反码，并在反码下计算 $1+(−2)$ ，最后将结果从反码转化回原码，则可得到正确结果 $−1$ 。

\[ 1 + (-2) \]

\[ -> 0000 0001(反码) + 0111 1101(反码) \]

\[ = 0111 1110(反码) \]

\[ = 1000 0001(原码) \]

原因二：解决零的歧义性

问题：数字零的原码有 +0 和 −0 两种表示方式。这意味着数字零对应着两个不同的二进制编码，其可能会带来歧义。比如在条件判断中，如果没有区分正零和负零，则可能会导致判断结果出错。而如果我们想要处理正零和负零歧义，则需要引入额外的判断操作，其可能会降低计算机的运算效率。

解决方案：在反码的基础上引入补码。

负零的补码为 00000000 ，与正零的补码相同。这意味着在补码表示中只存在一个零，正负零歧义从而得到解决。在负零的反码基础上加 1 会产生进位，但 byte 类型的长度只有 8 位，因此溢出到第 9 位的 1 会被舍弃。也就是说，负零的补码为 00000000 ，与正零的补码相同。这意味着在补码表示中只存在一个零，正负零歧义从而得到解决。 \[ -0 --> 1000 0000 (原码) \]

\[ = 1111 1111(反码) \]

\[ = 1 0000 0000 (反码) \]

最后的疑问：$-128$是怎么来的？

回答：1字节整的范围是 $[-128, 127]$， $-128$ 是如何得到的呢？

区间$ [-127,+127]$ 内的所有整数都有对应的原码、反码和补码，并且原码和补码之间是可以互相转换的。

然而，补码 1000 0000 是一个例外，它并没有对应的原码。按照负数的原码 -> 反码 -> 补码规则，补码 1000 0000 的原码就是 0000 0000。这显然是矛盾的，因为该原码表示数字 0 ，它的补码应该是自身。计算机规定这个特殊的补码 10000000 就是 $-128$ 的补码。实际上，$ (−1)+(−127)$ 在补码下的计算结果就是 $-128$ 。

\[ (-127) + (-1) \]

\[ -> 1111 1111(原码) + 1000 0001(原码) \]

\[ = 1000 0000(反码) + 1111 1110(反码) \]

\[ = 1000 0001(补码) + 1111 1111(补码) \]

\[ = 1000 0000(补码) \]

上述的所有计算都是加法运算。这暗示着一个重要事实：计算机内部的硬件电路主要是基于加法运算设计的。

通过将加法与一些基本逻辑运算结合，计算机能够实现各种其他的数学运算。例如，计算减法 $a-b$ 可以转换为计算加法 $a + (-b)$；计算乘法和除法可以转换为计算多次加法或减法。

计算机使用补码的原因：

基于补码表示，计算机可以用同样的电路和操作来处理正数和负数加法，不需要设计特殊的硬件电路来处理减法。
并且无须特别处理正负零的歧义问题。这大大简化了硬件设计，提高了运算效率。

浮点数编码

问：int 和 float 长度相同，都是 4 bytes ，但为什么 float 的取值范围远大于 int ？

答：这非常反直觉，因为按理说 float 需要表示小数，取值范围应该变小才对。

实际上，这是因为浮点数 float 采用了不同的表示方式。记一个 32-bit 长度的二进制数为：

$ b_{31}b_{30}b_{29}...b_{2}b_{1}b_{0} $

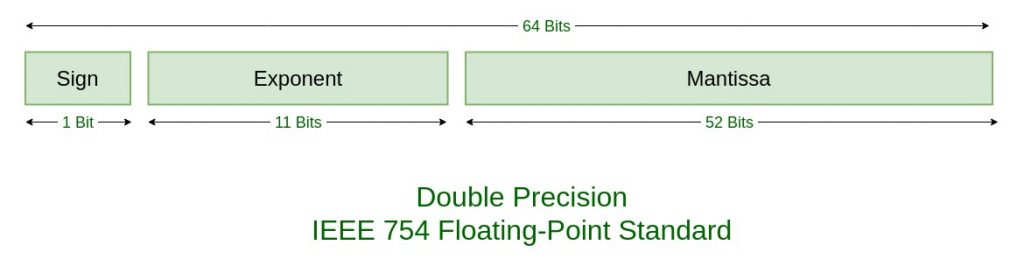
根据 IEEE 754 标准，32-bit 长度的 float 由以下三个部分构成。

符号位 S ：占 1 bit ，对应 $b_{31}$。
指数位 E ：占 8 bits ，对应 $b_{30}b_{29}...b_{23}$。
分数位 N ：占 23 bits ，对应 $b_{22}b_{21}...b_{0}$。

二进制数 float 对应的值的计算方法如下：

$S$、$E$、$N$ 的取值范围如下： \[ S \in \{0, 1\} \\ E \in \{1, 2, 3, 4, 5, ..., 254\} \\ 1 + N = (1 + \sum_{i=1}^{23}{b_{23-i}2^{-i}}) \subset [1+0, 1+(1-2^{-23})] = [1, 2-2^{-23}] \] 现在我们可以回答最初的问题：float 的表示方式包含指数位，导致其取值范围远大于 int 。根据以上计算，float 可表示的最大正数为 $2^{254-127} \times (2−2^{−23}) \approx 3.4 \times 1038$ ，切换符号位便可得到最小负数。

浮点数 float 扩展了取值范围，但其副作用是牺牲了精度。

整数类型 int 将全部 32 位用于表示数字，数字是均匀分布的；
而由于指数位的存在，浮点数 float 的数值越大，相邻两个数字之间的差值就会趋向越大。

指数位 $E=0$ 和 $E=255$ 具有特殊含义，用于表示零、无穷大、NaN 等。

指数位 E	分数位 $N = 0$	分数位 $N\neq 0$	计算公式
0	$\pm 0$	次正规数	$(-1)^s \times 2^{-127} \times (0 + N)$
1, 2, ..., 254	正规数	正规数	$(-1)^s \times 2^{E-127} \times (1 + N)$
255	$\pm \infty$	NaN	N/A

次正规数显著提升了浮点数的精度。最小正正规数为 $2^{−126}$ ，最小正次正规数为 $2^{−126} \times 2^{−23}$。

双精度 double 也采用类似 float 的表示方法（$S$、$E$、$N$ 的取值位范围如下图所示，详情见IEEE 745 standards），在此不做赘述。

字符编码

所有数据都是二进制数形式存储。
建立一套 “字符集”，规定每个字符和二进制数之间的一一对应关系。
计算机就可以通过“字符集”表完成二进制数到字符的转换。

ASCII

ASCII使用 7 位二进制数（即一个字节的低 7 位）表示一个字符，最多能够表示 128 个不同的字符。如图 3-6 所示，ASCII 码包括英文字母的大小写、数字 0 ~ 9、一些标点符号，以及一些控制字符（如换行符和制表符）。

ASCII 码仅能够表示英文。

GBK

中国国家标准总局于 1980 年发布了「GB2312」字符集，其收录了 6763 个汉字，基本满足了汉字的计算机处理需要。
「GBK」字符集是在 GB2312 的基础上扩展得到的，它共收录了 21886 个汉字。在 GBK 的编码方案中，ASCII 字符使用一个字节表示，汉字使用两个字节表示。

Unicode

「Unicode」的全称为 “统一字符编码”，理论上能容纳一百多万个字符。它致力于将全球范围内的字符纳入到统一的字符集之中，提供一种通用的字符集来处理和显示各种语言文字，减少因为编码标准不同而产生的乱码问题。
Unicode 是一种字符集标准，而非一种字符集，本质上是给每个字符分配一个编号（称为 “码点”），但它并没有规定在计算机中如何存储这些字符码点。如果使用定长的bit来存储字符，不同语种使用同样的长度，就会造成存储空间的浪费（英文字母只需要一个byte，中文需要两个byte，hello算法的Unicode标准编码数据如下：）。为解决上述问题，提出UTF-8编码。

UTF-8

UTF-8（8-bit Unicode Transformation Format）的编码规则并不复杂，分为以下两种情况。

对于长度为 1 字节的字符，将最高位设置为 0、其余 7 位设置为 Unicode 码点。值得注意的是，ASCII 字符在 Unicode 字符集中占据了前 128 个码点。也就是说，UTF-8 编码可以向下兼容 ASCII 码。这意味着我们可以使用 UTF-8 来解析年代久远的 ASCII 码文本。
对于长度为 $n$ 字节的字符（其中 $n > 1$），将首个字节的高 $n$ 位都设置为 1、第 $n+1$ 位设置为 0 ；从第二个字节开始，将每个字节的高 2 位都设置为 10 ；其余所有位用于填充字符的 Unicode 码点。
10能够起到校验符的作用，之所以将 10 当作校验符，是因为在 UTF-8 编码规则下，不可能有字符的最高两位是 10 。这个结论可以用反证法来证明：假设一个字符的最高两位是 10 ，说明该字符的长度为 1 ，对应 ASCII 码。而 ASCII 码的最高位应该是 0 ，与假设矛盾。
UTF-16 编码：使用 2 或 4 个字节来表示一个字符。所有的 ASCII 字符和常用的非英文字符，都用 2 个字节表示；少数字符需要用到 4 个字节表示。对于 2 字节的字符，UTF-16 编码与 Unicode 码点相等。
UTF-32 编码：每个字符都使用 4 个字节。这意味着 UTF-32 会比 UTF-8 和 UTF-16 更占用空间，特别是对于 ASCII 字符占比较高的文本。

hello算法的utf-8编码数据如下：

编程语言的字符编码

问：字符串在编程语言中的存储方式是怎样的？

答：对于以往的大多数编程语言，程序运行中的字符串都采用 UTF-16 或 UTF-32 这类等长的编码。

在等长编码下，我们可以将字符串看作数组来处理，这种做法具有以下优点。

随机访问: 由于每个部分等长，UTF-16 编码的字符串可以很容易地进行随机访问，时间复杂度为 $O(1)$。UTF-8 是一种变长编码，要找到第 $i$ 个字符，我们需要从字符串的开始处遍历到第 $i$ 个字符，这需要 $O(n)$ 的时间。
字符计数: 与随机访问类似，计算 UTF-16 字符串的长度也是 $O(1)$ 的操作。但是，计算 UTF-8 编码的字符串的长度需要遍历整个字符串。
字符串操作: 在 UTF-16 编码的字符串中，很多字符串操作（如分割、连接、插入、删除等）都更容易进行。在 UTF-8 编码的字符串上进行这些操作通常需要额外的计算，以确保不会产生无效的 UTF-8 编码。

实际上，编程语言的字符编码方案设计是一个很有趣的话题，其涉及到许多因素。

编程语言	默认字符编码方案
Java	Java 的 `String` 类型使用 UTF-16 编码，每个字符占用 2 字节。
JavaScript/TypeScript	JavaScript 和 TypeScript 的字符串使用 UTF-16 编码的原因与 Java 类似。
C#	C# 使用 UTF-16 编码，主要因为 .NET 平台是由 Microsoft 设计的，而 Microsoft 使用 UTF-16 编码。
Python	Python 中的 `str` 使用 Unicode 编码，并采用一种灵活的字符串表示，存储的字符长度取决于字符串中最大的 Unicode 码点。举个例子，若字符串中全部是 ASCII 字符，则每个字符占用 1 个字节；如果有字符超出了 ASCII 范围，但全部在基本多语言平面（BMP）内，则每个字符占用 2 个字节；如果有超出 BMP 的字符，则每个字符占用 4 个字节。
Go	Go 语言的 `string` 类型在内部使用 UTF-8 编码。Go 语言还提供了 `rune` 类型，它用于表示单个 Unicode 码点。
Rust	Rust 语言的 str 和 String 类型在内部使用 UTF-8 编码。Rust 也提供了 `char` 类型，用于表示单个 Unicode 码点。

由于Java等使用UTF-16编码，低估来字符数量，它们不得不采取 “代理对（一对 16 位的值）” 的方式来表示超过 16 位长度的 Unicode 字符。使用代理对存在如下缺点：

一方面，包含代理对的字符串中，一个字符可能占用 2 字节或 4 字节，从而丧失了等长编码的优势。
另一方面，处理代理对需要增加额外代码，这增加了编程的复杂性和 Debug 难度。

以上讨论的都是字符串在编程语言中的存储方式，这和字符串如何在文件中存储或在网络中传输是两个不同的问题。

hello algorithm

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

Fix the bug that latex formula does not render in hexo-fluid 上一篇

hello algorithm chapter 2 / space complexity 下一篇

指数位 E	分数位 \(N = 0\)	分数位 \(N\neq 0\)	计算公式
0	\(\pm 0\)	次正规数	\((-1)^s \times 2^{-127} \times (0 + N)\)
1, 2, ..., 254	正规数	正规数	\((-1)^s \times 2^{E-127} \times (1 + N)\)
255	\(\pm \infty\)	NaN	N/A