hello algorithm chapter 2 / space complexity
Reference: Hello 算法 空间复杂度
Overview
- space-complexity
- Difinition:算法占用内存空间随着输入数据量变大时的增长趋势
- 输入空间
- 暂存空间
- 暂存数据
- 栈帧空间
- 指令空间(ignored)
- 输出空间
- Deductive Method
- 最糟糕的输入:以最差输入数据为准
- 运行峰值:以算法运行中的峰值内存为准
- 注意统计栈帧空间
- Common types
- Constant order
- 暂存数据:数量与输入数据大小 n 无关的常量、变量、对象。
- 栈帧空间:循环中初始化变量或调用函数而占用的内存,在进入下一循环后就会被释放,因此不会累积占用空间,空间复杂度仍为O(1)
- Linear order
- 暂存数据:元素数量与n成正比的数组、链表、栈、队列等。
- 栈帧空间:此函数的递归深度为n,即同时存在n个未返回的 linear_recur() 函数,使用 O(n) 大小的栈帧空间。
- Square order
- 暂存数据:平方阶常见于矩阵和图,元素数量与n成平方关系。
- 栈帧空间:递归结构+数组
- Exponential order
- 暂存数据:指数阶常见于二叉树。观察图 2-19 ,高度为 \(n\) 的“满二叉树”的节点数量为 \(2^n−1\),占用 \(O(2^n)\) 空间。
- 栈帧空间
- Logarithmic order
- 暂存数据
- 栈帧空间:对数阶常见于分治算法。例如归并排序,输入长度为 n 的数组,每轮递归将数组从中点划分为两半,形成高度为 logn 的递归树,使用 n(logn) 栈帧空间。
Definition
算法占用内存空间随着输入数据量变大时的增长趋势
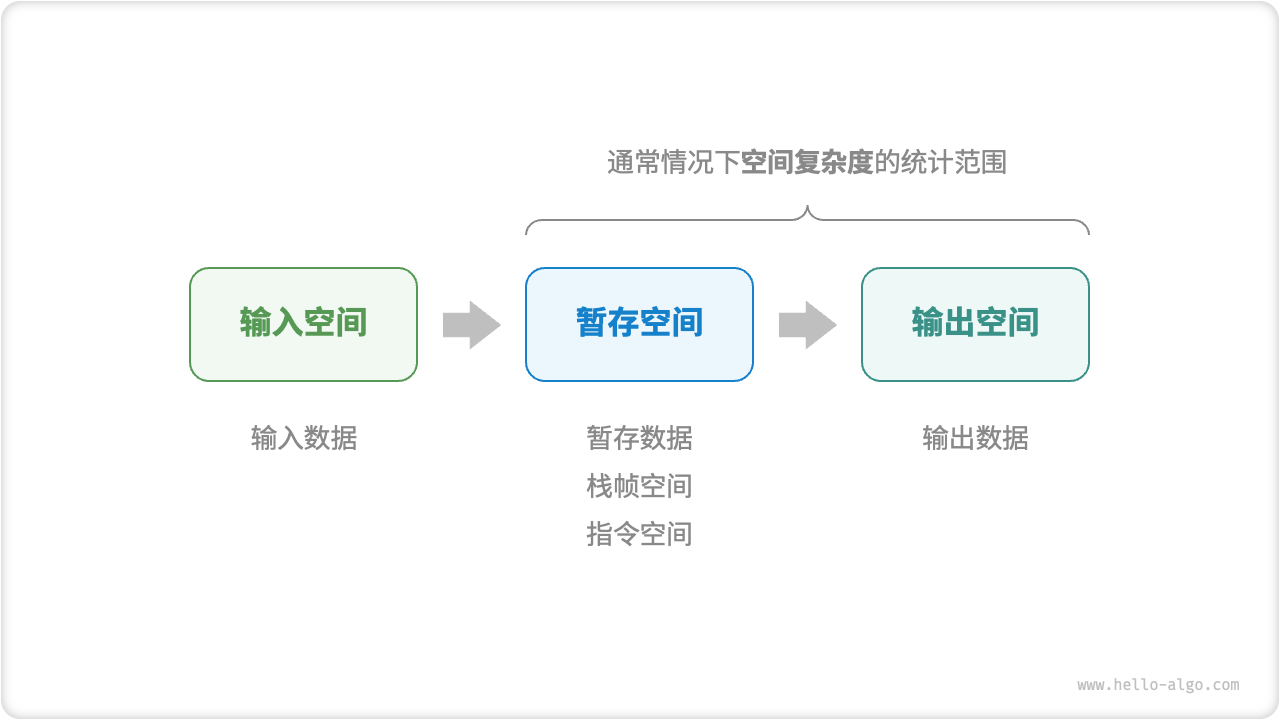
1 | |
Deductive Method
只关注最差空间复杂度。这是因为内存空间是一项硬性要求。
- 以最差输入数据为准。如果输入范围是1-10000,那就以10000为考虑输入。
- 以算法运行中的峰值内存为准。程序在执行最后一行之前,占用 \(O(1)\) 空间;当初始化数组 nums 时,程序占用 \(O(n)\) 空间;因此最差空间复杂度为 \(O(n)\)。
1 | |
- 在递归函数中,需要注意统计栈帧空间。例如:
- 函数 loop() 在循环中调用了 n 次 function() ,每轮中的 function() 都返回并释放了栈帧空间,因此空间复杂度仍为 \(O(1)\)。
- 递归函数 recur() 在运行过程中会同时存在 \(n\) 个未返回的 recur() ,从而占用 \(O(n)\) 的栈帧空间。
1 | |
Common types
\(O(1) < O(log n) < O(n) < O(n^2) < O(2^n)\)
Constant order
数量与输入数据大小 \(n\) 无关的常量、变量、对象。
循环中初始化变量或调用函数而占用的内存,在进入下一循环后就会被释放,因此不会累积占用空间,空间复杂度仍为\(O(1)\)。
1 | |
Square order
平方阶常见于矩阵和图,元素数量与 \(n\) 成平方关系。
1 | |
该函数的递归深度为 \(n\) ,在每个递归函数中都初始化了一个数组,长度分别为 \(n\)、\(n−1\)、…、\(2\)、\(1\),平均长度为 \(n/2\) ,因此总体占用 \(O(n^2)\) 空间:
1 | |
Exponential order
指数阶常见于二叉树。观察下图 ,高度为 \(n\) 的“满二叉树”的节点数量为 \(2^n - 1\),占用 \(O(2^n)\) 空间。
1 | |
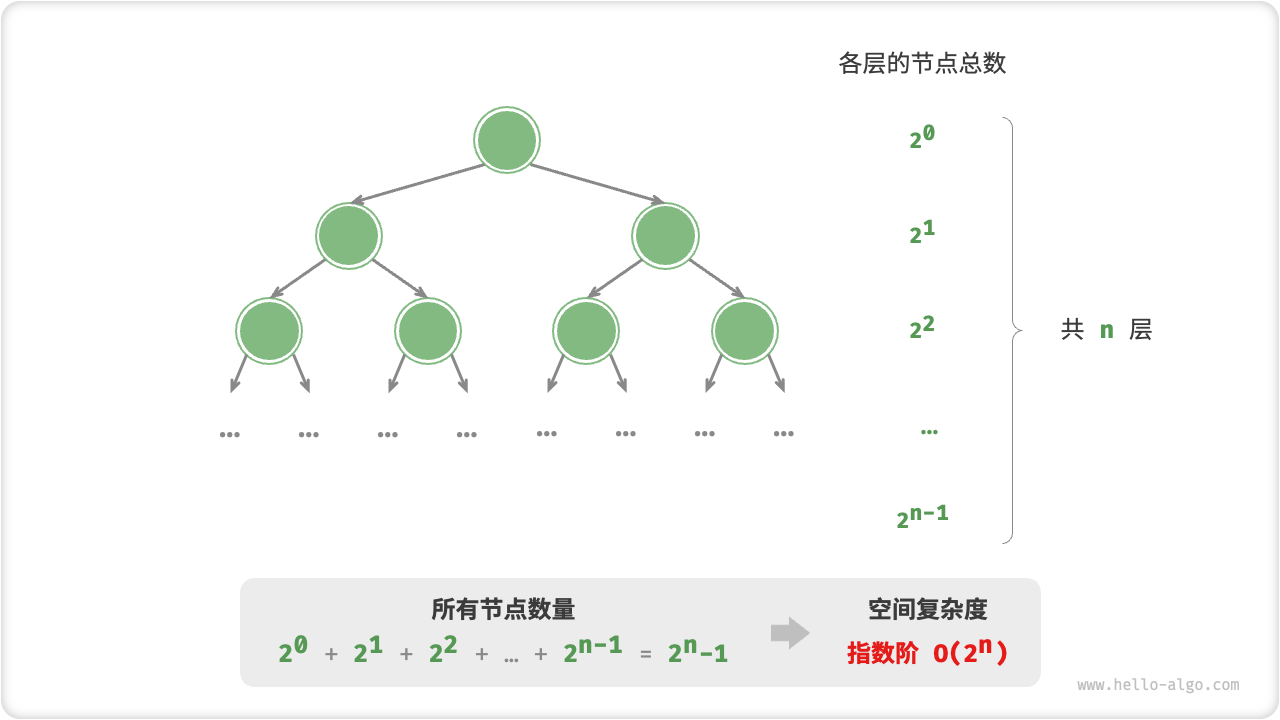
Logarithmic order
对数阶常见于分治算法。例如归并排序,输入长度为 \(n\) 的数组,每轮递归将数组从中点划分为两半,形成高度为 \(logn\) 的递归树,使用 \(n(logn)\) 栈帧空间。
Balance between space and time
降低时间复杂度通常需要以提升空间复杂度为代价,反之亦然。
牺牲内存空间来提升算法运行速度的思路称为“以空间换时间”;反之,则称为“以时间换空间”。
在数据量很大的情况下,控制空间复杂度也是非常重要的。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!