LeetCode 每日一题 0601-0607(2020)

2020-06-01 至 2020-06-07 LeetCode 每日一题

[0601] 1431. Kids With the Greatest Number of Candies（easy）

儿童节专题题目：1431.Kids With the Greatest Number of Candies(拥有最多糖果的孩子)

keyword：数组与指针

Question

Given the array candies and the integer extraCandies, where candies[i] represents the number of candies that the ith kid has.

For each kid check if there is a way to distribute extraCandies among the kids such that he or she can have the greatest number of candies among them. Notice that multiple kids can have the greatest number of candies.

Example 1: 

1
2
Input: candies = [2,3,5,1,3], extraCandies = 3
Output: [true,true,true,false,true]
Explanation: Kid 1 has 2 candies and if he or she receives all extra candies (3) will have 5 candies --- the greatest number of candies among the kids. Kid 2 has 3 candies and if he or she receives at least 2 extra candies will have the greatest number of candies among the kids. Kid 3 has 5 candies and this is already the greatest number of candies among the kids. Kid 4 has 1 candy and even if he or she receives all extra candies will only have 4 candies. Kid 5 has 3 candies and if he or she receives at least 2 extra candies will have the greatest number of candies among the kids.

Example 2: 

1
2
Input: candies = [4,2,1,1,2], extraCandies = 1
Output: [true,false,false,false,false]
Explanation: There is only 1 extra candy, therefore only kid 1 will have the greatest number of candies among the kids regardless of who takes the extra candy.

Example 3: 

1
2
Input: candies = [12,1,12], extraCandies = 10
Output: [true,false,true]
Constraints: 2 <= candies.length <= 100 1 <= candies[i] <= 100 1 <= extraCandies <= 50

Intuition

Children's day special, simple question. Find the maximum value firstly, and then walk through it to make judgment one by one.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

class Solution {
public:
    vector<bool> kidsWithCandies(vector<int>& candies, int extraCandies) {
        vector<bool> res;
        if(candies.empty())
            return res;
        // 求出candies的最大值
        int _max = *max_element(candies.begin(), candies.end());
        // 循环candies比较结果
        for(int i=0; i<candies.size(); i++){
            if(candies[i]+extraCandies>=_max){
                res.push_back(true);
            }else{
                res.push_back(false);
            }
        }
        return res;
    }
};

[0602] 面试题64. 求1+2+…+n

剑指offer 面试题64. 求1+2+…+n（中）

[0603] 837. New 21 Game（medium）

Question

837. 新21点

keyword：动态规划

Alice plays the following game, loosely based on the card game "21".

Alice starts with 0 points, and draws numbers while she has less than K points.  During each draw, she gains an integer number of points randomly from the range [1, W], where W is an integer.  Each draw is independent and the outcomes have equal probabilities.

Alice stops drawing numbers when she gets K or more points.  What is the probability that she has N or less points?

Example 1: 

1
2
Input: N = 10, K = 1, W = 10
Output: 1.00000
Explanation: Alice gets a single card, then stops.

Example 2: 

1
2
Input: N = 6, K = 1, W = 10
Output: 0.60000
Explanation: Alice gets a single card, then stops. In 6 out of W = 10 possibilities, she is at or below N = 6 points.

Example 3: 

1
2
Input: N = 21, K = 17, W = 10
Output: 0.73278
Note：0 <= K <= N <= 10000，1 <= W <= 10000。

Answers will be accepted as correct if they are within 10^-5 of the correct answer. The judging time limit has been reduced for this question.

Intuition

w: 抽牌范围为 0-w k: 抽牌条件得分小于k N: 计算得分小于等于N的概率

动态规划问题的求解分为三步

1、确定状态

Snipaste_2020-06-03_10-23-57

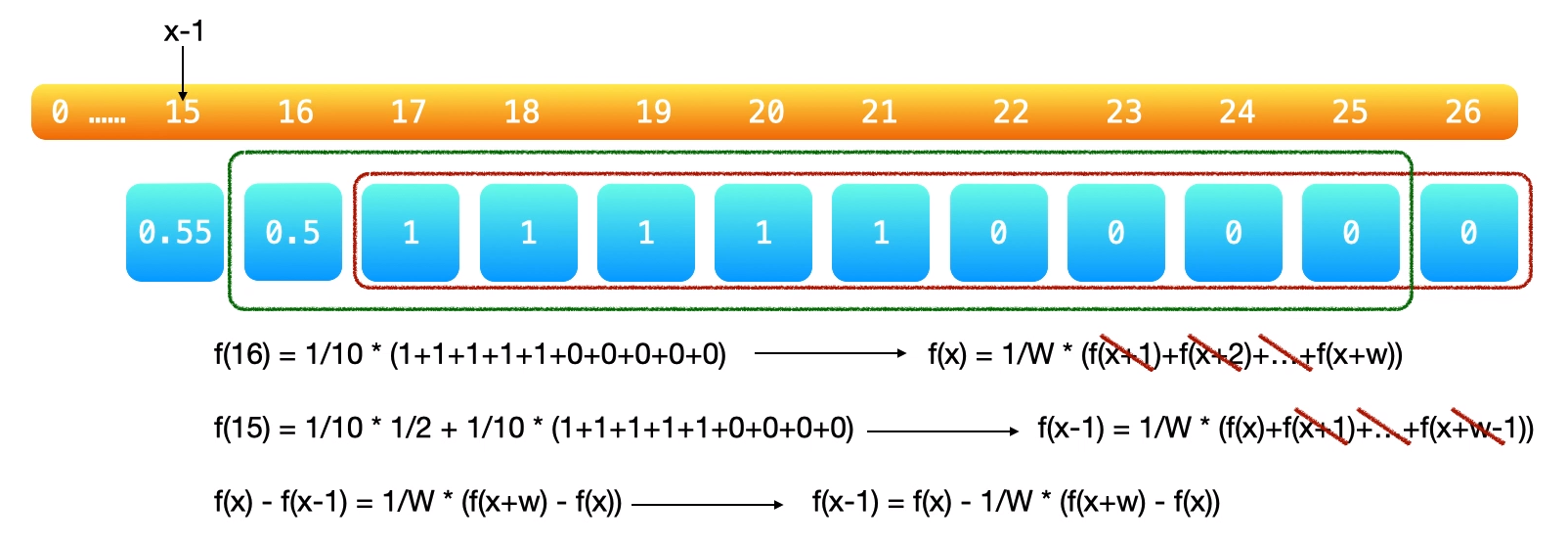
设 \(f(s)\) 为得分为 \(s\) 时，再抽取一次，新的得分小于等于 \(N\) 的概率。则爱丽丝以 0 分开始，并在她的得分少于 K 分时抽取数字，爱丽丝的分数不超过 N 的概率就是 \(f(0)\) 。以 N = 21, K = 17, W = 10，为例子\(f(16) = \frac{1}{10} \times (1+1+1+1+1+0+0+0+0+0)=\frac{}{}\) 。第一个 \(+1\) 代表抽到 \(1\) 之后，新得分（17）小于等于 \(N\) （21）的概率为 \(1\)（也就是100%）。同理，第二个 \(+1\) 代表抽到 \(2\) 之后，新得分（18）小于等于 \(N\)（21）的概率为 \(1\)（也就是100%）。第一个 \(+0\) 代表抽到 \(6\) 之后，新得分（22）小于等于 \(N\) （21）的概率为 \(0\)，以此类推。则上述过程可公式化为 \(f(s) = \frac{1}{w} \times f(s+1) + f(s+2) + ... + f(s+w)\)。

2、确定状态转移方程

Snipaste_2020-06-03_10-23-39

\(f(15) = \frac{1}{10} \times (\frac{1}{2} + 1 + 1 + 1 + 1 + 1 + 0 + 0 + 0 + 0)\)。第一个 \(+\frac{1}{2}\) 代表抽到 \(1\) 之后，新得分（16）小于等于 \(N\) （21）的概率为 \(f(16)=\frac{1}{2}\)。第一个 \(+1\) 代表抽到 \(2\) 之后，新得分（17）小于等于 \(N\) （21）的概率为 \(1\)（也就是100%）。综上，可得状态转移方程为：

\[ f(s-1) = \frac{1}{w} \times (f(s) + f(s) + ... + f(x+w-1)) \]

则，\(f(0) = \frac{1}{10} \times (f(1) + f(2) + ... + f(10))\)，从后（\(f(16)\) ）往前计算 \(f(0)\)。这里可以做个优化，\(f(s)\) 和 \(f(s-1)\) 之间存在重复部分，去掉重复部分之后，状态转移方程为： \[ f(s-1) = f(s) - \frac{1}{w} \times (f(s+w) - f(s)) \] Snipaste_2020-06-03_10-50-18

3、确定初始化状态

由于是从后往前计算，所以要初始化一个 k+w 的数组，初始化为0。然后，再将 k-N （17-21）部分改为 1。接着计算 k-1 位置（ \(f(16)\) ）的值， f(k-1) = min(N - K + 1, W) / w ，min(N - K + 1, W) 为 \(f(16)\) 要 \(+1\) 的个数，N = 21, K = 17, W = 10 时，min(N - K + 1, W)=5，也就是 \(f(16)\) \(+1\) 的个数为 \(5\)，最终 \(f(16) = \frac{5}{10} = \frac{1}{2}\)/。

完成以上步骤之后，就可以从\(k-2\)往前，利用 \(f(s-1) = f(s) - \frac{1}{w} \times (f(s+w) - f(s))\) 计算 \(f(0)\) 了。

复杂度分析

时间复杂度：\(O(\min(N, K+W))\)。即需要计算的 dp 值的数量 \(\min(N, K+W-1)\)。 空间复杂度：\(O(K+W)\)。创建了一个长度为 \(K+W+1\) 的数组 dp。

参考连接

LeetCode-Solution

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

class Solution {
public:
    double new21Game(int N, int K, int W) {
        if(K==0){
            return 1.0;
        }
        vector<double> dp(K+W+1);  // 通过vector<int> dp(length); 可以声明一个长度为length的数组。
        for(int i=K; i<=N && i<K+W; i++){
            dp[i] = 1.0;
        }
        dp[K-1] = 1.0 * min(N-K+1, W) / W;
        for(int i=K-2; i>=0; i--){
            dp[i] = dp[i+1] - (dp[i+1+W] - dp[i+1]) / W;
        }
        return dp[0];
    }
};

int main(){
    cout << "hello world" << endl;
    Solution so;
    cout << so.new21Game(21, 17, 10) << endl;
    int a;
    cin >> a;
}

[0604] 238. Product of Array Except Self (medium)

238.除自身以外数组的乘积

keyword: 数组与指针

Question

Given an array nums of n integers where n > 1, return an array output such that output[i] is equal to the product of all the elements of nums except nums[i].

Example: 

1
2
Input:  [1,2,3,4]
Output: [24,12,8,6]
Constraint: It's guaranteed that the product of the elements of any prefix or suffix of the array (including the whole array) fits in a 32 bit integer.(题目数据保证数组之中任意元素的全部前缀元素和后缀（甚至是整个数组）的乘积都在 32 位整数范围内。)

Note: Please solve it without division and in \(O(n)\).

Follow up: Could you solve it with constant space complexity (常数空间复杂度)? (The output array does not count as extra space for the purpose of space complexity analysis.)

Intuition

我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案，而是利用索引左侧所有数字的乘积和右侧所有数字的乘积（即前缀与后缀）相乘得到答案。

算法

  • 初始化两个空数组 L 和 R。对于给定索引 i，L[i] 代表的是 i 左侧所有数字的乘积，R[i] 代表的是 i 右侧所有数字的乘积。
  • 我们需要用两个循环来填充 L 和 R 数组的值。对于数组 L，L[0] 应该是 1，因为第一个元素的左边没有元素。对于其他元素：L[i] = L[i-1] * nums[i-1]。
  • 同理，对于数组 R，R[length-1] 应为 1。length 指的是输入数组的大小。其他元素：R[i] = R[i+1] * nums[i+1]。
  • 当 R 和 L 数组填充完成，我们只需要在输入数组上迭代，且索引 i 处的值为：L[i] * R[i]。

时间复杂度：\(O(N)\)，空间复杂度：\(O(N)\)。

由于输出数组不算在空间复杂度内，那么我们可以将 L 或 R 数组用输出数组来计算。先把输出数组当作 L 数组来计算，然后再动态构造 R 数组得到结果。让我们来看看基于这个思想的算法。

算法

  • 初始化 answer 数组，对于给定索引 i，answer[i] 代表的是 i 左侧所有数字的乘积。
  • 构造方式与之前相同，只是我们试图节省空间，先把 answer 作为方法一的 L 数组。
  • 这种方法的唯一变化就是我们没有构造 R 数组。而是用一个遍历来跟踪右边元素的乘积。并更新数组answer[i]=answer[i]。然后 R 更新为 R=R*nums[i]，其中变量 R 表示的就是索引右侧数字的乘积。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;


class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int length = nums.size();
        vector<int> res(length);
        res[0] = 1;
        for(int i=1; i<length; i++){
            res[i] = res[i-1] * nums[i-1];
        }
        // R 为右侧所有元素的乘积
        // 刚开始右边没有元素，所以 R = 1
        int R = 1;  // 变量 R 表示的就是索引右侧数字的乘积。
        for(int i=length-1; i>=0; i--){
            res[i] = res[i] * R;
            R *= nums[i];
        }
    return res;
    }
};

int main(){
    cout << "hello world" << endl;
    vector<int> input = {1,2,3,4};
    Solution so;
    vector<int> res;
    res = so.productExceptSelf(input);
    for(int i=0; i<res.size(); i++){
        cout << res[i] << endl;
    }
    int a;
    cin >> a;
}

[0605] 54. Spiral Matrix (easy)

LeetCode 54. 螺旋矩阵（中）& 剑指offer 面试题29. 顺时针打印矩阵

keyword: 数组与指针

[0606] 128. Longest Consecutive Sequence (hard)

最长连续序列

keyword: 数组与指针，并查集

Question

Given an unsorted array of integers, find the length of the longest consecutive elements sequence. Your algorithm should run in \(O(n)\) complexity.

示例: 

1
2
Input: [100, 4, 200, 1, 3, 2]
Output: 4
Explanation: The longest consecutive elements sequence is [1, 2, 3, 4]. Therefore its length is 4.

Intuition

方法一

初始化的时候先把数组里每个元素初始化为他的下一个数； 并的时候找他能到达的最远的数字就可以了。

方法二

用一个哈希表存储数组中的数，这样查看一个数是否存在即能优化至 \(O(1)\) 的时间复杂度。

仅仅是这样我们的算法时间复杂度最坏情况下还是会达到 \(O(n^2)\)（即外层需要枚举 \(O(n)\) 个数，内层需要暴力匹配 \(O(n)\) 次），无法满足题目的要求。但仔细分析这个过程，我们会发现其中执行了很多不必要的枚举，如果已知有一个 \(x, x+1, x+2, \cdots, x+y\) 的连续序列，而我们却重新从 \(x+1，x+2\)或者是 \(x+y\) 处开始尝试匹配，那么得到的结果肯定不会优于枚举 \(x\) 为起点的答案，因此我们在外层循环的时候碰到这种情况跳过即可。那么怎么判断是否跳过呢？由于我们要枚举的数 \(x\) 一定是在数组中不存在前驱数 \(x-1\) 的，不然按照上面的分析我们会从 \(x-1\) 开始尝试匹配，因此我们每次在哈希表中检查是否存在 \(x-1\) 即能判断是否需要跳过了。

增加了判断跳过的逻辑之后，时间复杂度是多少呢？外层循环需要 \(O(n)\) 的时间复杂度，只有当一个数是连续序列的第一个数的情况下才会进入内层循环，然后在内层循环中匹配连续序列中的数，因此数组中的每个数只会进入内层循环一次。根据上述分析可知，总时间复杂度为 \(O(n)\)，符合题目要求。

Code

  • 方法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<vector>
#include<iostream>
#include<unordered_map>

using namespace std;  

class Solution {
public:
    unordered_map<int,int> a,b;
    int find(int x){
        return a.count(x)?a[x]=find(a[x]):x;
    }
    int longestConsecutive(vector<int>& nums) {
        for(auto i:nums)
            a[i]=i+1;
        int ans=0;
        for(auto i:nums){
            int y=find(i+1);
            ans=max(ans,y-i);
        }
        return ans;
    }
};
  • 方法二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int> num_set;
        for (const int& num : nums) {
            num_set.insert(num);
        }

        int longestStreak = 0;

        for (const int& num : num_set) {
            if (!num_set.count(num - 1)) {
                int currentNum = num;
                int currentStreak = 1;

                while (num_set.count(currentNum + 1)) {
                    currentNum += 1;
                    currentStreak += 1;
                }

                longestStreak = max(longestStreak, currentStreak);
            }
        }

        return longestStreak;           
    }
};

[0607] Word Ladder II (hard)

单词接龙 II

keyword: 广度优先搜索、回溯算法

Question

Given two words (beginWord and endWord), and a dictionary's word list, find all shortest transformation sequence(s) from beginWord to endWord, such that:

Only one letter can be changed at a time Each transformed word must exist in the word list. Note that beginWord is not a transformed word. Note:

Return an empty list if there is no such transformation sequence. All words have the same length. All words contain only lowercase alphabetic characters. You may assume no duplicates in the word list. You may assume beginWord and endWord are non-empty and are not the same.

Example 1: 

1
2
3
4
Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
Output: 
1
2
3
4
[
  ["hit","hot","dot","dog","cog"],
  ["hit","hot","lot","log","cog"]
]
Example 2: 
1
2
3
4
Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]
Output: 
1
[]
Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.

Intuition

本题要求的是最短转换序列，看到最短首先想到的就是 BFS。想到 BFS 自然而然的就能想到图，但是本题并没有直截了当的给出图的模型，因此我们需要把它抽象成图的模型。

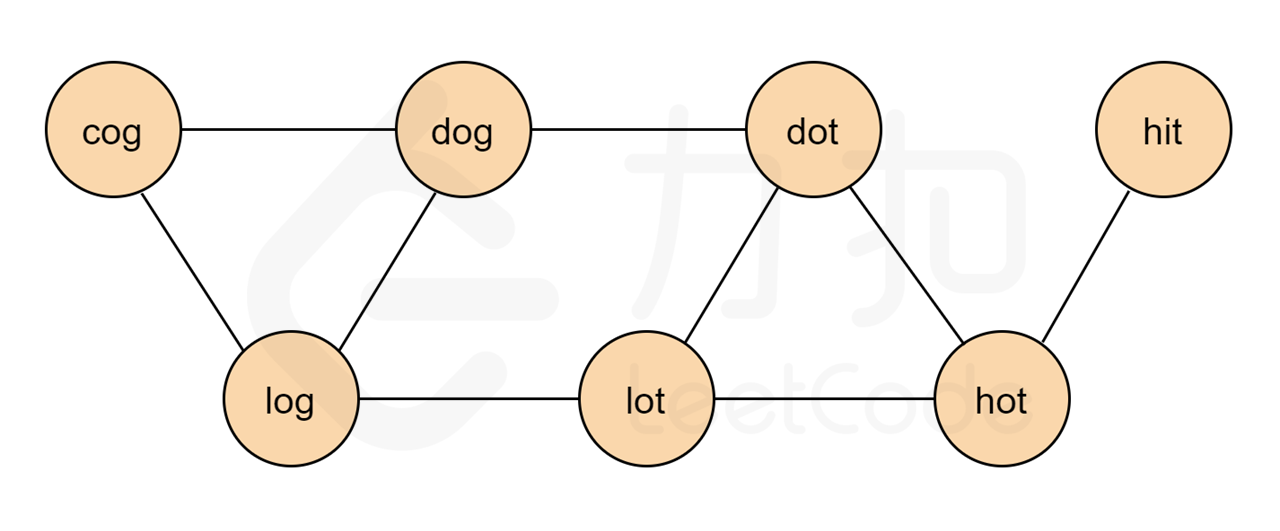
我们可以把每个单词都抽象为一个点，如果两个单词可以只改变一个字母进行转换，那么说明他们之间有一条双向边。因此我们只需要把满足转换条件的点相连，就形成了一张图。根据示例 1 中的输入，我们可以建出下图：

126_fig1

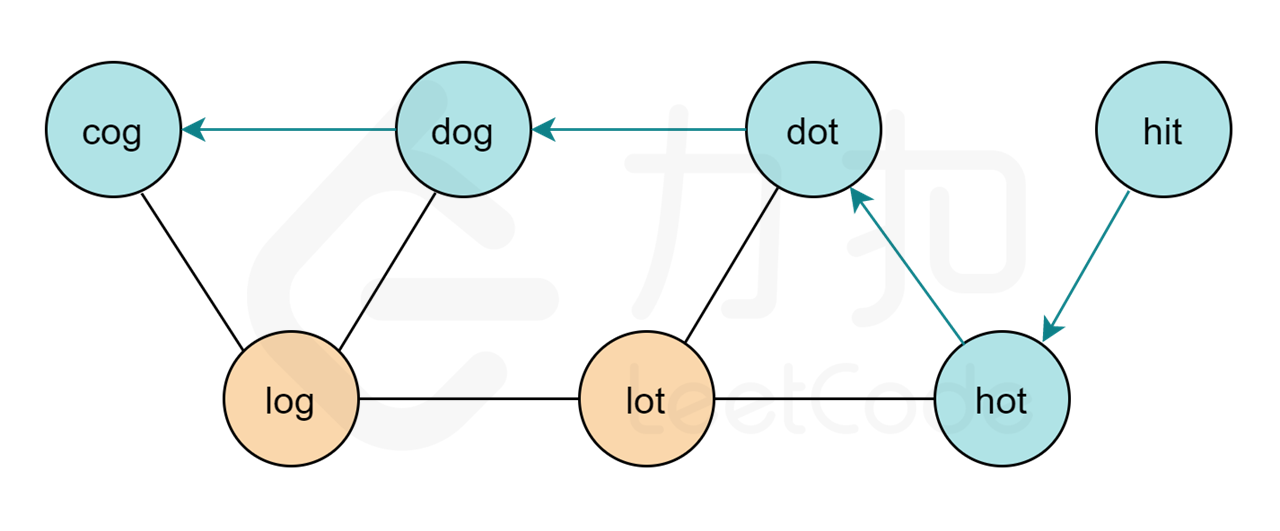
基于该图，我们以 hit 为图的起点， 以cog 为终点进行广度优先搜索（BFS），寻找 hit 到 cog 的最短路径。下图即为答案中的一条路径。

126_fig2

时间复杂度：\(O(N^2 \times C)\)。其中 \(N\) 为 wordList 的长度，\(C\) 为列表中单词的长度。构建映射关系的时间复杂度为 \(O(N)\)。建图首先两层遍历 wordList，复杂度为 \(O(N^2)\)，里面比较两个单词是否可以转换的时间复杂度为 \(O(C)\)，总的时间复杂度为 \(O(N^2\times C)\)。广度优先搜索的时间复杂度最坏情况下是 \(O(N^2)\)，因此总时间复杂度为 \(O(N^2 \times C)\)

空间复杂度：\(O(N^2)\)，其中 \(N\) 为 wordList 的大小。数组和哈希表的复杂度都为 \(O(N)\)，图 edges 的复杂度最坏为 \(O(N^2)\)。广度优先搜索队列的复杂度最坏情况下，即每两个路径都有很多重叠的节点时，也是 \(O(N^2)\)，因此总的空间复杂度为 \(O(N^2)\)。

拓展

由于本题起点和终点固定，所以可以从起点和终点同时开始进行双向广度优先搜索，可以进一步降低时间复杂度。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
const int INF = 1 << 20;

class Solution {
private:
    unordered_map<string, int> wordId;
    vector<string> idWord;
    vector<vector<int>> edges;
public:
    vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {
        int id = 0;
        for (const string& word : wordList) {
            if (!wordId.count(word)) {
                wordId[word] = id++;
                idWord.push_back(word);
            }
        }
        if (!wordId.count(endWord)) {
            return {};
        }
        if (!wordId.count(beginWord)) {
            wordId[beginWord] = id++;
            idWord.push_back(beginWord);
        }
        edges.resize(idWord.size());
        for (int i = 0; i < idWord.size(); i++) {
            for (int j = i + 1; j < idWord.size(); j++) {
                if (transformCheck(idWord[i], idWord[j])) {
                    edges[i].push_back(j);
                    edges[j].push_back(i);
                }
            }
        }
        const int dest = wordId[endWord];
        vector<vector<string>> res;
        queue<vector<int>> q;
        vector<int> cost(id, INF);
        q.push(vector<int>{wordId[beginWord]});
        cost[wordId[beginWord]] = 0;
        while (!q.empty()) {
            vector<int> now = q.front();
            q.pop();
            int last = now.back();
            if (last == dest) {
                vector<string> tmp;
                for (int index : now) {
                    tmp.push_back(idWord[index]);
                }
                res.push_back(tmp);
            } else {
                for (int i = 0; i < edges[last].size(); i++) {
                    int to = edges[last][i];
                    if (cost[last] + 1 <= cost[to]) {
                        cost[to] = cost[last] + 1;
                        vector<int> tmp(now);
                        tmp.push_back(to);
                        q.push(tmp);
                    }
                }
            }
        }
        return res;
    }

    bool transformCheck(const string& str1, const string& str2) {
        int differences = 0;
        for (int i = 0; i < str1.size() && differences < 2; i++) {
            if (str1[i] != str2[i]) {
                ++differences;
            }
        }
        return differences == 1;
    }
};