LeetCode 103. 二叉树的锯齿形层次遍历（中）& 剑指offer 面试题32 III. 从上到下打印二叉树 III

总结一下，两个栈，一个栈保存当前层要打印的节点，另一个栈保存下一层要打印的节点。所有节点都打印完了，就交换这两个节点，打印下一层。另外，在奇数层要先左后右的扫描下一层的节点，在偶数层要先右后左的扫描下一层。

Question

给定一个二叉树，返回其节点值的锯齿形层次遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

例如：给定二叉树 [3, 9, 20, null, null, 15, 7], 

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7
返回锯齿形层次遍历如下： 
1
2
3
4
5
[
  [3],
  [20,9],
  [15,7]
]

测试用例

功能测试（完全二叉树；所有节点只有左子树的二叉树；所有节点只有右子树的二叉树）。 特殊输入测试（二叉树根节点为nullptr指针；只有一个节点的二叉树）。

本题考点

考查应聘者的思维能力。按之字形遍历二叉树，这对很多应聘者来说是一个新概念，要在短时间内想明白遍历的过程不是一件容易的事情。应聘者通过具体的例子找出其中的规律并想到基于两个栈的算法，是解决这个问题的关键。 考查应聘者对二叉树及栈的理解。

Intuition

当二叉树的根节点（节点1）打印之后，它的左子节点（节点2）和右子节点（节点3）先后保存到一个数据容器里。

在打印第二层的节点时，先打印节点3，再打印节点2。看起来节点在这个数据容器里是后进先出的，因此这个数据容器可以用栈来实现。

接着打印第二层的两个节点。根据之字形顺序，先打印节点3，再打印节点2，并把它们的子节点保存到一个数据容器里。我们注意到在打印第三层的时候，先打印节点2的两个子节点（节点4和节点5），再打印节点3的两个子节点（节点6和节点7）。这意味着我们仍然可以用一个栈来保存节点2和节点3的子节点。

1.png

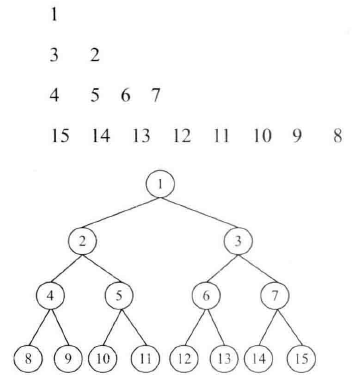
总结一下，两个栈，一个栈保存当前层要打印的节点，另一个栈保存下一层要打印的节点。所有节点都打印完了，就交换这两个节点，打印下一层。另外，在奇数层要先左后右的扫描下一层的节点，在偶数层要先右后左的扫描下一层。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

# 总结一下，两个栈，一个栈保存了当前层要打印的节点，另一个栈保存下一层要打印的节点。
# 所有节点都打印完了，就交换这两个节点，打印下一层。
# 另外，在奇数层要先左后右的扫描下一层的节点，在偶数层要先右后左的扫描下一层。
class Solution:
    def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:
        if root == None:
            return []
        res = []
        tmp = []
        current_stack = []
        next_stack = []
        current_stack.append(root)
        flag = True  # 是否在奇数层
        while len(current_stack):
            node = current_stack.pop()
            if node:
                tmp.append(node.val)
                if flag:  # 奇数层要先左后右的扫描下一层的节点
                    if node.left: next_stack.append(node.left)
                    if node.right: next_stack.append(node.right)
                else:  # 在偶数层要先右后左的扫描下一层。
                    if node.right: next_stack.append(node.right)
                    if node.left: next_stack.append(node.left)
            if len(current_stack) == 0:
                res.append(tmp[:])
                tmp = []
                current_stack = next_stack[:]
                next_stack = []
                flag = not flag
        return res