考查应聘者的发散思维能力。这道题目有两种常规解法：一种是把所有数字都相乘再分别除以各个数字，但题目已经限定不能使用除法；另一种解法是连乘 n-1 个数字得到 B[i]。通常面试官会告知应聘者还有比 \(O(n^2)\) 更高效的算法。此时应聘者不能放弃，还要继续打开思路，多角度去分析解答问题。

Question

给定一个数组 A[0,1,…,n-1]，请构建一个数组 B[0,1,…,n-1]，其中 B 中的元素 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。

示例:

输入: [1,2,3,4,5]
输出: [120,60,40,30,24]

提示： 所有元素乘积之和不会溢出 32 位整数 a.length <= 100000

测试用例

功能测试（输入数组包含正数、负数、一个0、多个0）。 边界值测试（输入数组的长度为0）。

本题考点

考查应聘者的发散思维能力。这道题目有两种常规解法：一种是把所有数字都相乘再分别除以各个数字，但题目已经限定不能使用除法；另一种解法是连乘 n-1 个数字得到 B[i]。通常面试官会告知应聘者还有比 \(O(n^2)\) 更高效的算法。此时应聘者不能放弃，还要继续打开思路，多角度去分析解答问题。 考查应聘者对数组的理解和编程能力。

Intuition

可以把 B[i]=A[0]×A[1]…×A[i-1]×A[i+1]…×A[n-1] 看成 A[0]×A[1]…×A[i-1] 和 A[i+1]…×A[n-1] 两部分的乘积。因此，数组 B 可以用一个矩阵来创建。在下图中，B[i] 为矩阵中第i 行所有元素的乘积。

Snipaste_2020-05-18_11-42-48

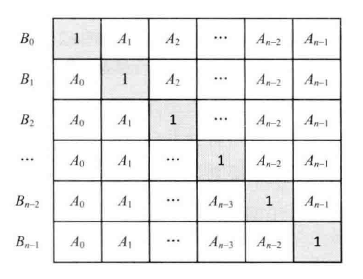
不妨定义C[i]=A[0]×A[1]×…×A[i-2]×A[i-1]，D[i]=A[i+1]×…×A[n-2]×A[n-1]。 C[i]可以用自上而下的顺序计算出来，即 C[i]=C[i-1]×A[i-1]，其中 C[i-1]=A[0]×A[1]×…×A[i-2]。类似的 D[i]，也可以用自下而上的顺序计算出来，即D[i]=D[i+1]×A[i+1]，其中D[i+1]=A[i+2]×…×A[n-2]×A[n-1]。

时间复杂度： \(O(N)\) ，其中 \(N\) 为数组长度，两轮遍历数组 \(a\) ，使用 \(O(N)\) 时间。
空间复杂度： \(O(N)\) ，变量 B[] 和 C[] 使用 n 大小额外空间。

Code

• 我的解法

class Solution:
    def constructArr(self, a: List[int]) -> List[int]:
        # 计算长度length
        length = len(a)
        if length < 1:
            return []

        # 定义C[i]=A[0]×A[1]×…×A[i-2]×A[i-1]
        # 自上而下计算 C[i]
        # 即 C[i]=C[i-1]×A[i-1]，其中 C[i-1]=A[0]×A[1]×…×A[i-2]。
        C = [1]
        for row in range(1, length):
            C =  C + [C[row-1] * a[row-1]]

        # 定义D[i]=A[i+1]×…×A[n-2]×A[n-1]
        # 自下而上计算 D[i]
        # 即D[i]=D[i+1]×A[i+1]，其中D[i+1]=A[i+2]×…×A[n-2]×A[n-1]。
        D = [1]
        for row in range(length-2, -1, -1):
            D = [D[0] * a[row + 1]] + D

        # 计算 B[i]
        # B[i] = C[i] * D[i]
        B = [0] * length
        for row in range(length):
            B[row] = C[row] * D[row]

        return B

该解法通过不了LeetCode最后的那个超长的 TestCase，说明空间复杂度太大也会通过不了测试用例。

• Krahets大佬解法

class Solution:
    def constructArr(self, a: List[int]) -> List[int]:
        b, tmp = [1] * len(a), 1
        for i in range(1, len(a)):
            b[i] = b[i - 1] * a[i - 1] # 下三角
        for i in range(len(a) - 2, -1, -1): 
            tmp *= a[i + 1] # 上三角
            b[i] *= tmp # 下三角 * 上三角
        return b

时间复杂度： \(O(N)\) ，其中 \(N\) 为数组长度，两轮遍历数组 \(a\) ，使用 \(O(N)\) 时间。
空间复杂度： \(O(1)\) ，变量 tmp 使用常数大小额外空间（数组 b 作为返回值，不计入复杂度考虑）。

作者：Krahets 链接：https://leetcode-cn.com/problems/gou-jian-cheng-ji-shu-zu-lcof/solution/mian-shi-ti-66-gou-jian-cheng-ji-shu-zu-biao-ge-fe/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。