剑指offer 面试题59 - I. 滑动窗口的最大值（易）& LeetCode 239. 滑动窗口最大值（难）

考查应聘者的知识迁移能力。如果应聘者深入理解了滑动窗口最大值和队列最大值之间的联系，那么掌握了上述两道题中任意一道题的解法，就能顺利解答另外一道题。巧用 while，一个 while 可以代替很多 if 条件判断。

Question

给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

示例:

1
2
3
4
5
6
7
8
9
10
11
12
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7] 
解释: 

  滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

提示：

你可以假设 k 总是有效的，在输入数组不为空的情况下，1 ≤ k ≤ 输入数组的大小。

测试用例

功能测试（输入数组的数字大小无序；输入数组的数字单调递增；输入数组的数字单调递减）。 边界值测试（滑动窗口的大小为0、1、等于输入数组的长度、大于输入数组的长度）。 特殊输入测试（输入数组为空）。

本题考点

考查应聘者分析问题的能力。无论是求滑动窗口的最大值还是求队列的最大值，都不是一道容易的面试题，应聘者可以通过举例的方法一步步分析，找出其中的规律。 考查应聘者的知识迁移能力。如果应聘者深入理解了滑动窗口最大值和队列最大值之间的联系，那么掌握了上述两道题中任意一道题的解法，就能顺利解答另外一道题。

Intuition

依次遍历

从第 \(0\) 位到第 \(n-k\) 位依次遍历即可求出每个滑动窗口里的最大值。时间复杂度为 \(O((n-k) \times k)\)，空间复杂度为 \(O(n-k)\)。

辅助队列方法

设置一个辅助队列，保存最大值对应下标，动态调整其中的值，保证每次遍历，队首的元素都是当前的最大值。以数组 [2, 3, 4, 2, 6, 2, 5, 1]、滑动窗口长度为 3 为例。

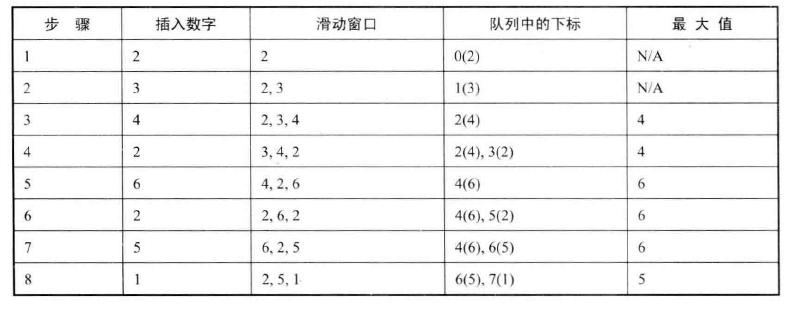
Snipaste_2020-05-16_15-02-45

第 3 个数字 4，此时，窗口大小满足3，可以输出最大值。每次都输出以队首元素为下标的元素。 第 4 个数字 2，2比队列中的数字4小。当4滑出窗口之后，2还是有可能成为滑动窗口中的最大值，因此把2存入队列的尾部，此时最大值4位于队列的头部。 第 5 个数字是 6，由于它比队列中已有的两个数字4和2都大，因此这时4和2已经不可能成为滑动窗口中的最大值了。先把4和2从队列中删除，再把数字6存入队列。这时候最大值6仍然位于队列的头部。 第 6 个数字是 2，由于它比队列中已有的数字6小，2还是有可能成为滑动窗口中的最大值，所以把2也存入队列的尾部。此时队列中有两个数字，其中最大值6位于队列的头部。 第 7 个数字是 5，在队列中已有的两个数字6和2里，2小于5，因此2不可能是一个滑动窗口的最大值，可以把它从队列的尾部删除。删除数字2之后，再把数字5存入队列。此时队列里剩下两个数字6和5，其中位于队列头部的是最大值6。 最后一个数字是 1，把1存入队列的尾部。注意到位于队列头部数字6是数组的第五个0数字，此时的滑动窗口已经不包括这个数字了，比应该把数字6从队列中删除。其中最大值5位于队列的头部。

那么怎么知道滑动窗口中的数字是否从窗口中滑出呢？ 在队列里存入数字在数组里的下标，而不是数值。当队首的下标与当前处理的数字的下标之差大于或者等于滑动窗口的大小时，这个数经从窗口中滑出，可以从队列中删除了。

将一个数字的下标存入队列，应该做什么？ 在存入一个数字的下标之前，首先要判断队列里已有数字是否小于待存入的数字。如果已有的数字小于待存入的数字，那么这些数字已经不可能是滑动窗口的最大值，因此它们将会被依次从队列的尾部删除（调用函数pop_back）。同时，如果队列头部的数字已经从窗口里滑出，那么滑出的数字也需要从队列的头部删除（调用函数pop_front）。由于队列的头部和尾部都有可能删除数字，这也是需要两端开口的队列的原因。

时间复杂度为 \(O(n-k)\)，空间复杂度为 \(O(n-k)\)，用于保存 \(n-k\) 个最大值。

Code

依次遍历

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        if not nums or k < 1:  return []
        start = 0
        end = start + k
        res = []
        while end <= len(nums):
            windows = nums[start:end]
            res.append(max(windows))
            start += 1
            end += 1
        return res

辅助队列方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        if not nums or k < 1:  return []
        queue = []
        res = []
        for i in range(len(nums)):
            # 当队首的下标与当前处理的数字的下标之差大于或者等于滑动窗口的大小时，
            # 这个数经从窗口中滑出，可以从队列中删除了。
            if len(queue) != 0 and i - queue[0] >= k:
                del queue[0]

            # 简洁处理法
            while len(queue) != 0 and nums[i] > nums[queue[-1]]:
                queue.pop()
            queue.append(i)

            # # 复杂处理法 注意对照找差距
            # # 如果队列为空就直接入队到队首。
            # if len(queue) == 0:
            #     queue.append(i)
            # # 当前值大于等于队首数字，就清空队列，将当前值的下标入队到队首。
            # elif nums[i] >= nums[queue[0]]:
            #     queue = [i]
            # # 当前值小于队首元素，那么就找到合适的位置将其放进去。
            # else:
            #     for j in range(len(queue)-1, -1, -1):
            #         if nums[queue[j]] <= nums[i]:
            #             queue.pop()
            #     queue.append(i)

            # 窗口长度达标即可添加最大值。
            if i >= k - 1:
                res.append(nums[queue[0]])

        return res

Extension

Question

面试题59 - II. 队列的最大值

请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是 \(O(1)\)。

若队列为空，pop_front 和 max_value 需要返回 -1

示例 1： 

1
2
3
4
输入: 
["MaxQueue","push_back","push_back","max_value","pop_front","max_value"]
[[],[1],[2],[],[],[]]
输出: [null,null,null,2,1,2]
示例 2： 
1
2
3
4
输入: 
["MaxQueue","pop_front","max_value"]
[[],[],[]]
输出: [null,-1,-1]
限制： \(1\) <= push_back,pop_front,max_value的总操作数 <= \(10000\) \(1\) <= value <= \(10^5\)

Intuition

实际上，除非使用链表，否则，无论如何，最坏时间复杂度都不能达到 \(O(1)\)，这里是目标是将均摊时间复杂度都降到 \(O(1)\)。

双队列解法：我们知道对于一个普通队列，push_back 和 pop_front 的时间复杂度都是 \(O(1)\)，因此我们直接使用队列的相关操作就可以实现这两个函数。对于 max_value 函数，我们通常会这样思考，即每次入队操作时都更新最大值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class MaxQueue:

    def __init__(self):
    	self.queue = []
		self.max_value = -(1<<32)

    def max_value(self) -> int:
    	return max_value

    def push_back(self, value: int) -> None:
    	if value > self.max_value:
    		self.max_value = value
    	self.queue.appen(value)
    
    def pop_front(self) -> int:
    	tmp = self.queue[0]
    	del self.queue[0]
    	return tmp

但是当出队时，这个方法会造成信息丢失，即当最大值出队后，我们无法知道队列里的下一个最大值。

为了解决上述问题，我们只需记住当前最大值出队后，队列里的下一个最大值即可。 具体方法是使用一个双端队列 deque，在每次入队时

  • 如果 deque 队尾元素小于即将入队的元素 value，则将小于 value 的元素全部出队后，再将 value 入队；
  • 如果 deque 队尾元素大于等于即将入队的元素 value。

这时，辅助队列 deque 队首元素就是队列的最大值。

Complexity

时间复杂度：\(O(1)\)（插入，删除，求最大值） 删除操作于求最大值操作显然只需要 \(O(1)\) 的时间。 而插入操作虽然看起来有循环，做一个插入操作时最多可能会有 \(n\) 次出队操作。但要注意，由于每个数字只会出队一次，因此对于所有的 \(n\) 个数字的插入过程，对应的所有出队操作也不会大于 \(n\) 次。因此将出队的时间均摊到每个插入操作上，时间复杂度为 \(O(1)\)。 空间复杂度：\(O(n)\)，需要用队列存储所有插入的元素。

preference

作者：腐烂的橘子 链接：https://leetcode-cn.com/problems/dui-lie-de-zui-da-zhi-lcof/solution/ru-he-jie-jue-o1-fu-za-du-de-api-she-ji-ti-by-z1m/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

Test Case

往队列末尾插入不同大小的数字并求最大值；从队列头部删除数字并求最大值。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class MaxQueue:

    def __init__(self):
        self.queue = []
        self.dequeue = []

    def max_value(self) -> int:
        return self.dequeue[0] if self.dequeue else -1

    def push_back(self, value: int) -> None:
        self.queue.append(value)
        while self.dequeue and self.dequeue[-1] <= value:
            self.dequeue.pop()
        self.dequeue.append(value)

    def pop_front(self) -> int:
        if not self.queue: return -1
        ans = self.queue[0]
        del self.queue[0]
        if ans == self.dequeue[0]:
            del self.dequeue[0]
        return ans