剑指offer 面试题51. 数组中的逆序对（难）

考查应聘者分析复杂问题的能力。统计逆序对的过程很复杂，如何发现逆序对的规律，是应聘者解决这道题目的关键。

Question

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1: 

1
2
输入: [7,5,6,4]
输出: 5
限制：0 <= 数组长度 <= 50000

测试用例

功能测试（输入未经排序的数组、递增排序的数组、递减排序的数组；输入的数组中包含重复的数字）。 边界值测试（输入的数组中只有两个数字；输入的数组中只有一个数字）。 特殊输入测试（表示数组的指针为 nullptr 指针）。

本题考点

考查应聘者分析复杂问题的能力。统计逆序对的过程很复杂，如何发现逆序对的规律，是应聘者解决这道题目的关键。 考查应聘者对归并排序的掌握程度。如果应聘者在分析统计逆序对的过程中发现问题与归并排序的相似性，并能基于归并排序形成解题思路，那通过这轮面试的概率就很大了。

Intuition

基于归并思想的方法

  1. 先把数组分隔成子数组（最小到两个数字组成的子数组），统计出子数组内部的逆序对的数目，数组内部排序，以免之后的统计过程中重复统计逆序对。
  2. 然后再统计出两个相邻子数组之间的逆序对的数目。
  3. 在统计逆序对的过程中，还需要对数组进行排序。

如果对排序算法很熟悉，那么我们不难发现这个排序的过程实际上就是归并排序，以数组 [7, 5, 6, 4] 为例：

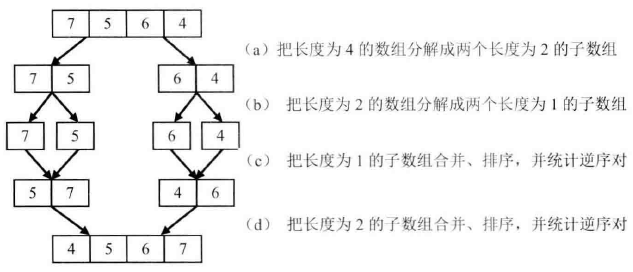
Snipaste_2020-05-13_20-54-19
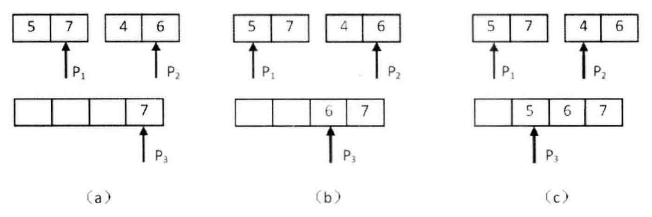
Snipaste_2020-05-13_20-54-29

（a）P1指向的数字大于P2指向的数字，表明数组中存在逆序对。P2指向的数字是第二个子数组的第二个数字，因此第二个子数组中有两个数字比7小，把逆序对数目加2。并把7复制到辅助数组，向前移动P1和P3。 （b）P1指向的数字小于P2指向的数字，没有逆序对。把P2指向的数字复制到辅助数组，并向前移动P2和P3。（c）P1指向的数字大于P2指向的数字，因此存在逆序对。由于P2指向的数字是第二个子数组的第一个数字，子数组中只有一个数字比5小，把逆序对数目加1。并把5复制到辅助数组，向前移动P1和P3。

可以发现，我们先用两个指针分别指向两个子数组的末尾，P1指向位置靠前的数组，P2指向位置靠后的数组，并每次比较两个指针指向的数字。如果第一个子数组中的数字大于第二个子数组中的数字，则构成逆序对，并且逆序对的数目等于第二个子数组中剩余数字的个数，如图（a）和图（c）所示。如果第一个数组中的数字小于或等于第二个数组中的数字，则不构成逆序对，如图（b）所示。每次比较的时候，我们都把较大的数字从后往前复制到一个辅助数组，确保辅助数组中的数字是递增排序的。在把较大的数字复制到辅助数组之后，把对应的指针向前移动一位，接下来进行下一轮比较。

时间复杂度和归并排序一样都是\(O(nlogn)\) ，空间复杂度为 \(O(n)\)。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution:
    def reversePairs(self, nums: List[int]) -> int:
        def countReversePairs(nums, copy, start, end):
            if start == end:
                copy[start] = nums[start]
                return 0
            length = (end - start) // 2
            left = countReversePairs(copy, nums, start, start+length)
            right = countReversePairs(copy, nums, start+length+1, end)
            # i为前半段最后一个数字的下标 P1
            i = start + length
            # j为后半段最后一个数字的下标 P2
            j = end
            indexCopy = end  # P3
            count = 0
            # 比较 P1 和 P2 判断是否存在逆序
            while i >= start and j >= start + length + 1:
                if nums[i] > nums[j]:  # 出现逆序
                    copy[indexCopy] = nums[i]  # 先赋值
                    indexCopy -= 1  # 后递减
                    i -= 1
                    count += (j - start - length)
                else:  # 没有逆序
                    copy[indexCopy] = nums[j]  # 先赋值
                    indexCopy -= 1  # 后递减
                    j -= 1
            # 调整copy序列的顺序，实现排序，以免之后的统计过程中重复统计逆序对。
            while i >= start:
                copy[indexCopy] = nums[i]  # 先赋值
                indexCopy -= 1  # 后递减
                i -= 1
            while j >= start + length + 1:  # 先赋值
                copy[indexCopy] = nums[j]  # 后递减
                indexCopy -= 1
                j -= 1

            return left + right + count

        if not nums:
            return 0

        copy = []
        for i in nums:
            copy.append(i)
        count = countReversePairs(nums, copy, 0, len(nums)-1)

        return count