自定义一种新的遍历算法来解决
Question
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。 但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的: 示例 1: | 输入:root = [1,2,2,3,4,4,3]
输出:true
|
| 输入:root = [1,2,2,null,3,null,3]
输出:false
|
测试用例
功能测试(对称的二叉树;因结构而不对称的二叉树;结构对称但节点的值不对称的二叉树)。 特殊输入测试(二叉树的根节点为nullptr指针;只有一个节点的二叉树;所有节点的值都相同的二叉树)。
本题考点
考查应聘者对二叉树的理解。本题实质上是利用树的遍历算法解决问题。 考查应聘者的思维能力。树的对称是一个抽象的概念,应聘者需要在短时间内想清楚判断对称的步骤并转换为代码。应聘者可以通过画图把抽象的问题形象化,这有助于其快速找到解题思路。
Intuition
 Snipaste_2020-05-09_11-03-12.png
Snipaste_2020-05-09_11-03-12.png
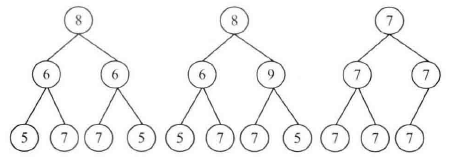
针对前序遍历定义一种对称遍历算法,即先遍历父节点,再遍历它的右子节点,最后遍历它的左子节点。这样一来,如果一棵树是对称的,那么它的前序遍历和对称遍历的结果就会是一样的。图中的第一棵二又树, 则遍历序列是{8, 6, 5, 7, 6, 7, 5}。如果用我们定义的针对前序遍历的对称遍历算法, 则得到的对称遍历序列是{8, 6, 5, 7, 6, 7, 5}。我们注意到这两个序列是一样的,也就是说,第一棵树是镜像对称的。图中第二棵二叉树的前序遍历序列为{8, 6, 5, 7, 9, 7, 5}, 而相应的对称前序遍历序列为{8, 9, 5, 7, 6, 7, 5}。在这两个序列中, 第二步和第五步是不一样的,也就是说第二课树不是对称的。
陷阱
第三棵二又树有些特殊, 它所有节点的值都是一样的。它的前序遍历序列是{7, 7, 7, 7, 7, 7}, 前序遍历的对称遍历序列也是{7, 7, 7, 7, 7, 7}。这两个序列是一样的, 可显然第三棵二叉树不是对称的。怎样才能正确地判断这种类型的二叉树呢?只要我们在遍历二叉树时把遇到的 nullptr 指针也考虑进来就行了。
Code
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public:
bool symmetricCompare(TreeNode* root1, TreeNode* root2){
if(root1 == NULL && root2 == NULL)
return true;
if(root1 == NULL || root2 == NULL)
return false;
if(root1->val != root2->val)
return false;
return symmetricCompare(root1->left, root2->right) && symmetricCompare(root1->right, root2->left);
}
bool isSymmetric(TreeNode* root) {
return symmetricCompare(root, root);
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| class Solution {
public:
vector<int> preOrder(TreeNode* pRoot){
if(pRoot==NULL){
vector<int> res = {0x7fffffff};
return res;
}
vector<TreeNode*> treeStack;
vector<int> output;
TreeNode* pNode = pRoot;
while(pNode !=NULL || treeStack.size() > 0){
while(pNode !=NULL){
treeStack.push_back(pNode);
output.push_back(pNode->val);
pNode = pNode->left;
if(pNode==NULL){
output.push_back(0x7fffffff);
}
}
if(treeStack.size() > 0){
pNode = treeStack.back();
treeStack.pop_back();
pNode = pNode->right;
if(pNode==NULL){
output.push_back(0x7fffffff);
}
}
}
return output;
}
vector<int> mirrorPreOrder(TreeNode* pRoot){
if(pRoot==NULL){
vector<int> res = {0x7fffffff};
return res;
}
vector<TreeNode*> treeStack;
vector<int> output;
TreeNode* pNode = pRoot;
while(pNode !=NULL || treeStack.size() > 0){
while(pNode !=NULL){
treeStack.push_back(pNode);
output.push_back(pNode->val);
pNode = pNode->right;
if(pNode==NULL){
output.push_back(0x7fffffff);
}
}
if(treeStack.size() > 0){
pNode = treeStack.back();
treeStack.pop_back();
pNode = pNode->left;
if(pNode==NULL){
output.push_back(0x7fffffff);
}
}
}
return output;
}
bool isSymmetric(TreeNode* root) {
vector<int> preList = preOrder(root);
vector<int> mirrorList = mirrorPreOrder(root);
if(preList==mirrorList)
return true;
return false;
}
};
|
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution:
def symmetricCompare(self, root1, root2):
if root1 == None and root2 == None:
return True
if root1 == None or root2 == None:
return False
if root1.val != root2.val:
return False
return self.symmetricCompare(root1.left, root2.right) and self.symmetricCompare(root1.right, root2.left)
def isSymmetric(self, root: TreeNode) -> bool:
return self.symmetricCompare(root, root)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| class Solution:
def isSymmetric(self, pRoot):
preList = self.preOrder(pRoot)
mirrorList = self.mirrorPreOrder(pRoot)
if preList == mirrorList:
return True
return False
def preOrder(self, pRoot):
if pRoot == None:
return [None]
treeStack = []
output = []
pNode = pRoot
while pNode or len(treeStack) > 0:
while pNode:
treeStack.append(pNode)
output.append(pNode.val)
pNode = pNode.left
if not pNode:
output.append(None)
if len(treeStack):
pNode = treeStack.pop()
pNode = pNode.right
if not pNode:
output.append(None)
return output
def mirrorPreOrder(self, pRoot):
if pRoot == None:
return [None]
treeStack = []
output = []
pNode = pRoot
while pNode or len(treeStack) > 0:
while pNode:
treeStack.append(pNode)
output.append(pNode.val)
pNode = pNode.right
if not pNode:
output.append(None)
if len(treeStack):
pNode = treeStack.pop()
pNode = pNode.left
if not pNode:
output.append(None)
return output
|
