LeetCode 142. 环形链表 II(中)& 剑指offer 面试题23. 链表中环的入口
2020腾讯暑期实习一面题目,LeetCode 142. 环形链表(易)的升级版,需要输出循环开始位置。
链表、双指针
LeetCode官方题解 题目来源:力扣(LeetCode)
题目
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
示例 1:
1 | |
解释:链表中有一个环,其尾部连接到第二个节点。
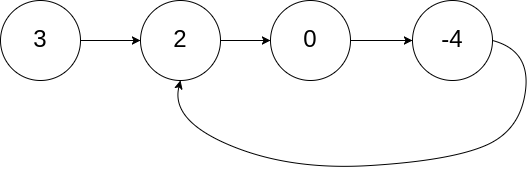
示例 2:
1 | |
解释:链表中有一个环,其尾部连接到第一个节点。
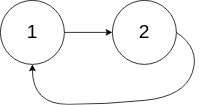
示例 3: 1
2输入:head = [1], pos = -1
输出:no cycle
进阶:你是否可以不用额外空间解决此题?
测试用例
功能测试(链表中包含或者不包含环;链表中有多个或者只有一个节点)。 特殊输入测试(链表头节点为nullptr指针)。
直觉
基于Hash Map
基于hash表检查第一个之前就被访问过的节点,将其返回。
时间复杂度:\(O(n)\),对于含有 n 个元素的链表,我们访问每个元素最多一次。添加一个结点到哈希表中只需要花费 \(O(1)\) 的时间。 空间复杂度:\(O(n)\),空间取决于添加到哈希表中的元素数目,最多可以添加 \(n\) 个元素
Folyd算法
第一阶段 执行 第141题 代码,利用快慢指针从head出发,慢指针一次走一步,快指针一次走两步,找到相遇点。
第二阶段 给定阶段 1 找到的相遇点,阶段 2 将找到环的入口。首先我们初始化额外的两个指针: ptr1 ,指向链表的头(下图中的 list head), ptr2 指向相遇点(下图中的 first interaction)。然后,我们每次将它们往前移动一步,直到它们相遇,它们相遇的点就是环的入口,返回这个节点。上述推断的基础是:关系 \(b = F\) 成立。
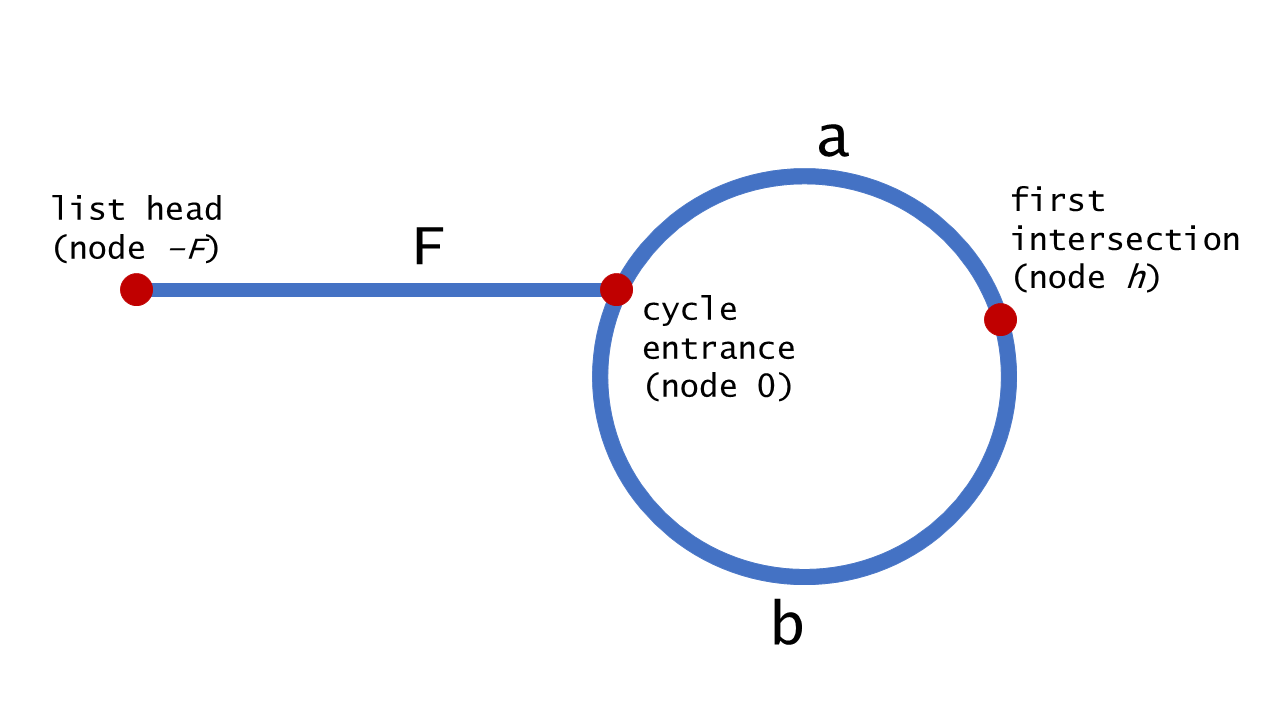
关于上面这个结论的数学推导过程如下:当快慢指针都是从head出发时,假设相遇时慢指针走了 \(x\) 步,快指针走了 \(y\) 步,则相遇时有 \(2 \times x = y\),已知 \(x=F+a\), \(y = F + a + b\),代入前式可得 \(F = b\)。以上就是Floyd算法的全过程了。
时间复杂度:\(O(n)\) 对有环列表,快指针和慢指针在 \(F+C-h\) 次迭代以后会指向同一个节点,正如上面正确性证明所示,\(F+C-h \leq F+C = n\),所以阶段 1 运行时间在 \(O(n)\) 时间以内,阶段 2 运行 \(F < n\) 次迭代,所以它运行时间也在 \(O(n)\) 以内。 对于无环链表,快指针大约需要迭代 \(\dfrac{n}{2}\) 次会抵达链表的尾部,这样不会进入阶段 2 就直接退出。 因此,不管是哪一类链表,都会在与节点数成线性关系的时间内运行完。
空间复杂度:\(O(1)\) Floyd 的快慢指针算法仅需要几个指针,所以只需常数级别的额外空间。
剑指offer
- 判断是否有环:执行 第141题 代码,利用快慢指针从head出发,慢指针一次走一步,快指针一次走两步,找到相遇点。
- 计算环部分的长度
n:如果两个指针相遇,则表明链表中存在环。两个指针相遇的节点一定是在环中。可以从这个节点出发,一边继续向前移动一边计数,当再次回到这个节点时,就可以得到环中节点数了。 - 找到环入口:快慢指针回到开始点,快指针领先慢指针
n个节点之后,快慢指针都以一次一步的方式向前移动,两个指针相遇之处,就是链表入口。
代码
基于hash map
1 | |
Floyd算法
1 | |
剑指offer
1 | |
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!