记录图和堆有关的基础概念及相关算法
图
图的基本概念
数据结构-图
无向完全图中,n 个点则有 n(n-1)/2 条边。 有向完全图中,n 个点则有 n(n-1) 条边。
图的遍历
v2-ee45526da273f5c0fde827480913e29e_720w
graph = {'a' : ['b' , 'c' ],'b' : ['a' , 'c' , 'd' ],'c' : ['a' ,'b' , 'd' ,'e' ],'d' : ['b' , 'c' , 'e' , 'f' ],'e' : ['c' , 'd' ],'f' : ['d' ]
DFS
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 def DFS (graph, s ):set ()while len (stack) > 0 :for node in nodes:if node not in seen:'a' )def DFS1 (graph, s, queue=[] ):for i in graph[s]:if i not in queue:return queue'a' )
BFS
:set ()while len (queue) > 0 :0 )for node in nodes:if node not in seen:'a' )
有权图中最短路径问题
v2-94d2ac8ba296ef97477b0001a996104a_720w
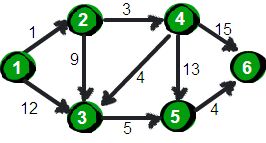
inf = float ('inf' )0 ,1 ,12 ,inf,inf,inf],0 ,9 ,3 ,inf,inf],0 ,inf,5 ,inf],4 ,0 ,13 ,15 ],0 ,4 ],0 ]]
Dijkstra算法
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。 迪杰斯特拉算法主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
这里我们需要用到三个辅助数组:
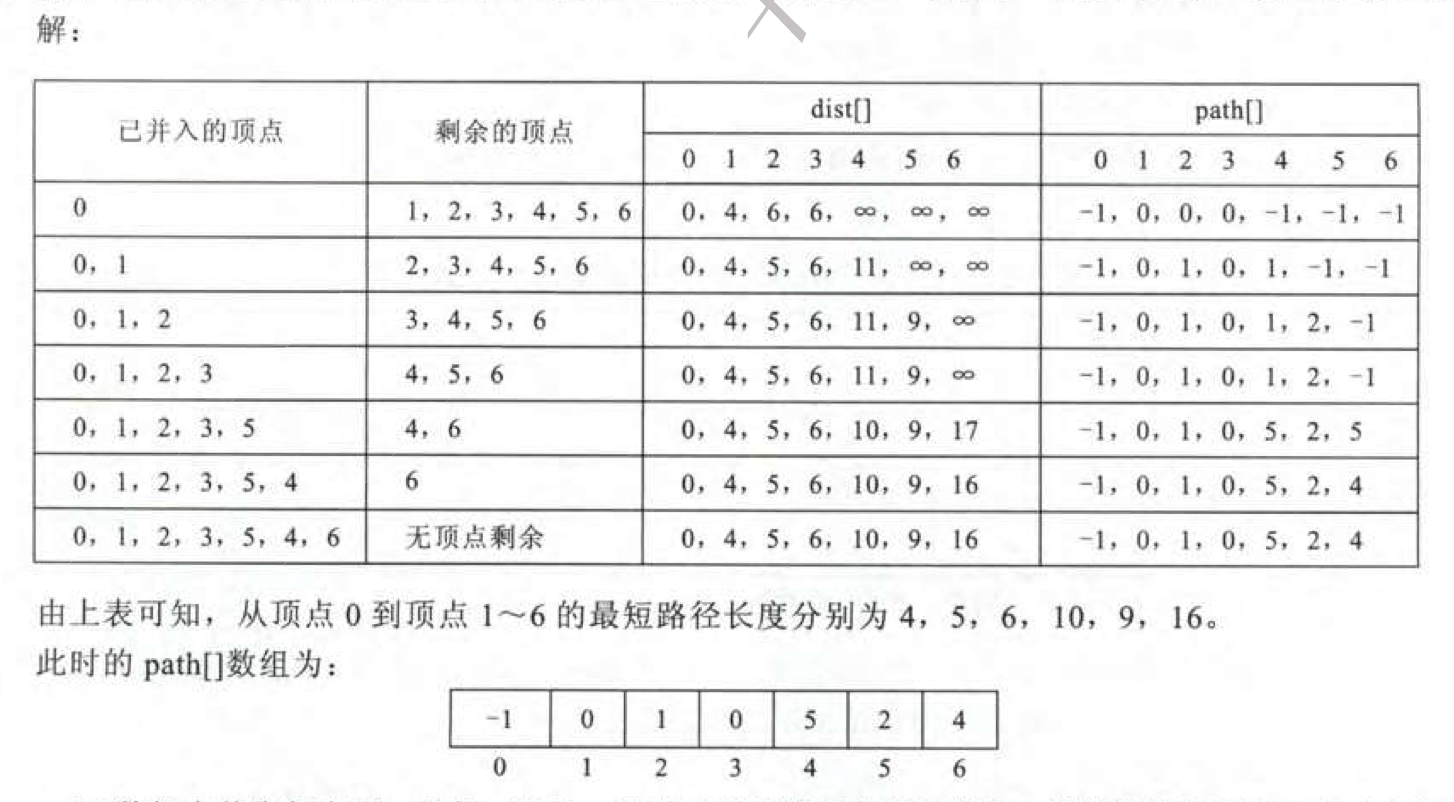
dist[vi],从 v0 到每个顶点 vi 的最短路径长度。path[vi],保存从 v0 到 vi 最短路径上的前一个顶点。set[],标记点是否被并入最短路径 。
执行过程:
初始化:
选定源点 v0。
dist[vi]:若 v0 到 vi 之间若存在边,则为边上的权值,否则为∞。
path[vi]:若 v0 到 vi 之间存在边,则 path[vi]=v0,否则为-1。
set[v0]=TRUE,其余为 FALSE。
执行:
从当前的 dist[]数组中选出最小值 dist[vu] 。
将 set[vu] 置为TRUE。
检测所有 set[vi]==FALSE 的点。
比较 dist[vi] 和 dist[vu]+w 的大小,w 为 <vu,vi>的权值。
如果 dist[vu]+w<dist[vi]
更新 path[] 并将 vu 加入路径中
直到遍历完所有的顶点(n-1次)
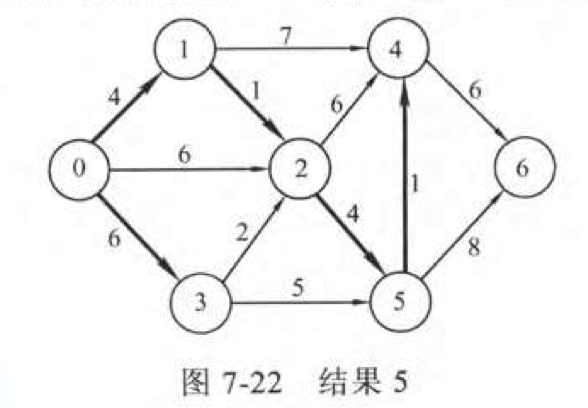
结合图来理解就是:
1139760-20181025102953586-1615580793
1139760-20181025103032940-108172764
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 def dijkstra (matrix_distance, source_node ):float ('inf' )len (dis)0 for i in range (node_nums)]1 for i in range (node_nums-1 ):min = inffor j in range (node_nums):if flag[j] == 0 and dis[j] < min :min = dis[j]1 for v in range (node_nums):if flag[v] == 0 and matrix_distance[u][v] < inf:if dis[v] > dis[u] + matrix_distance[u][v]:return dis0 )
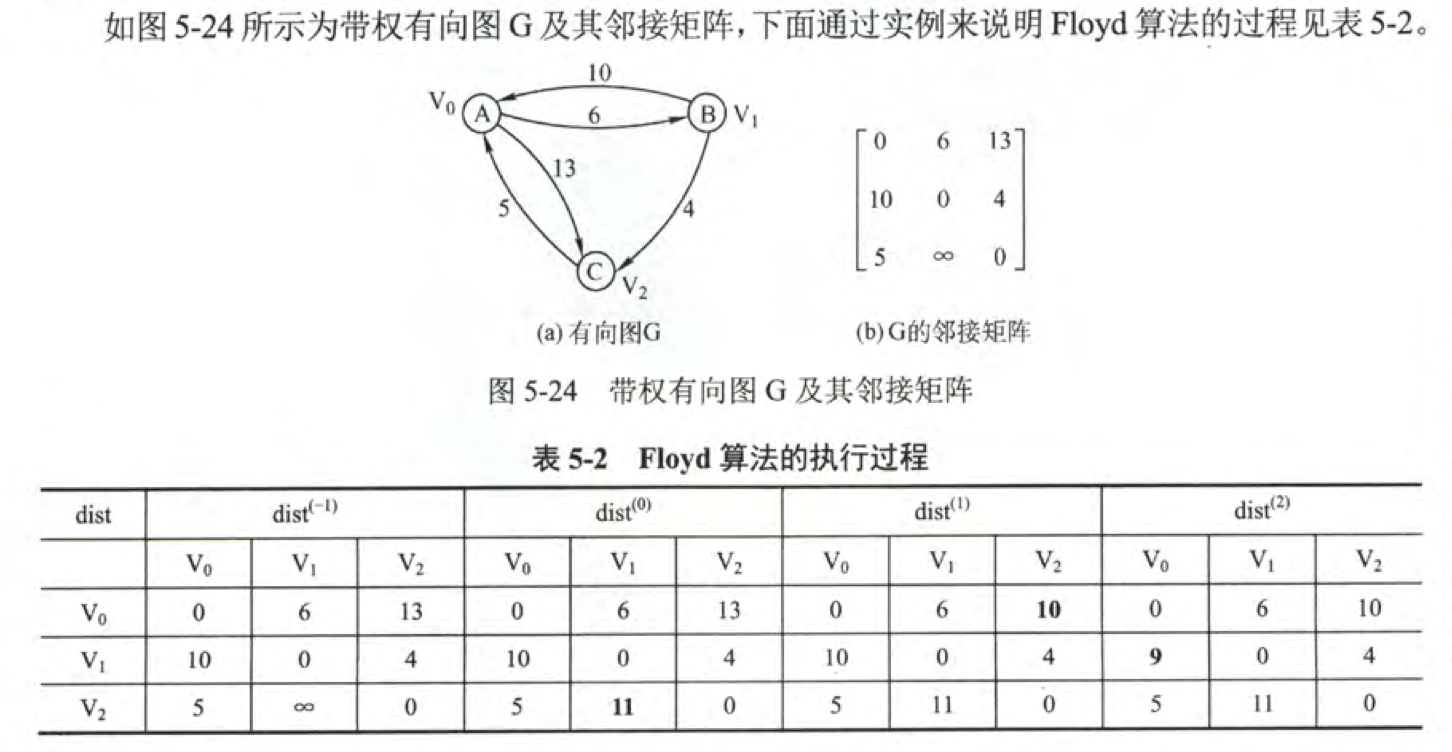
Floyd算法
Floyd算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法 ,与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
初始化一个矩阵 \(A\) ,\((A^{(-1)})[i][j]=G.edges[i][j]\) 。
迭代n轮:\((A^{(k)})=Min{(A^{(k-1)})[i][j], (A^{(k-1)})[i][k]+(A^{(k-1)})[k][j]}\)
\((A^{(k)})\) 矩阵存储了前K个节点之间的最短路径,基于最短路径的性质,第K轮迭代的时候会求出第K个节点到其他K-1个节点的最短路径。
1139760-20181025134249477-410650124
def Floyd (dis ):len (dis[0 ])for k in range (nums_vertex):for i in range (nums_vertex):for j in range (nums_vertex):if dis[i][j] > dis[i][k] + dis[k][j]:return dis
最小生成树问题
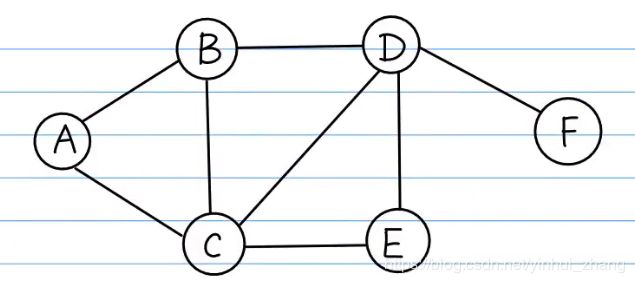
假设以下情景,有一块木板,板上钉上了一些钉子,这些钉子可以由一些细绳连接起来。假设每个钉子可以通过一根或者多根细绳连接起来,那么一定存在这样的情况,即用最少的细绳把所有钉子连接起来。 更为实际的情景是这样的情况,在某地分布着N个村庄,现在需要在N个村庄之间修路,每个村庄之前的距离不同,问怎么修最短的路,将各个村庄连接起来。 以上这些问题都可以归纳为最小生成树问题,用正式的表述方法描述为:给定一个无方向的带权图G=(V, E),最小生成树为集合T, T是以最小代价连接V中所有顶点所用边E的最小集合。 集合T中的边能够形成一颗树,这是因为每个节点(除了根节点)都能向上找到它的一个父节点。
解决最小生成树问题已经有前人开道,Prime算法和Kruskal算法,分别从点和边下手解决了该问题。
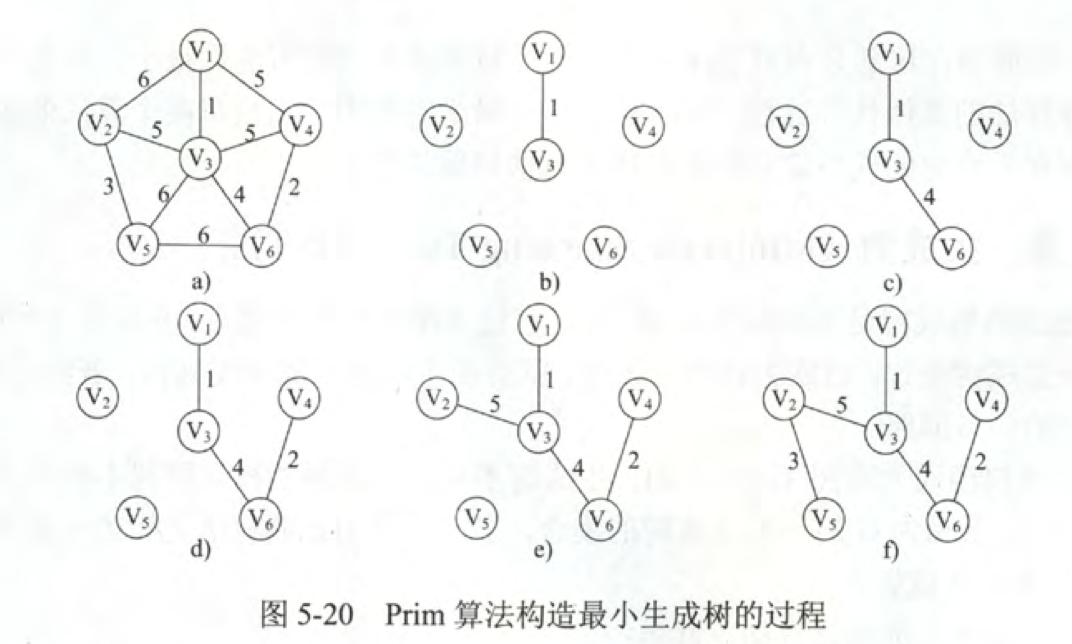
Prim算法
Prim算法是一种产生最小生成树的算法。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克(英语:Vojtěch Jarník)发现;并在1957年由美国计算机科学家罗伯特·普里姆(英语:Robert C. Prim)独立发现;1959年,艾兹格·迪科斯彻再次发现了该算法。
Prim算法从任意一个顶点开始,每次选择一个与当前顶点集最近的一个顶点,并将两顶点之间的边加入到树中。Prim算法在找当前最近顶点时使用到了贪婪算法。适合于边稠密的图。
算法描述
在一个加权连通图中,顶点集合V,边集合为E
任意选出一个点作为初始顶点,标记为visit,计算所有与之相连接的点的距离,选择距离最短的,标记visit.
重复以下操作,直到所有点都被标记为visit: 在剩下的点钟,计算与已标记visit点距离最小的点,标记visit,证明加入了最小生成树。
1139760-20181009152355508-535468775
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 from collections import defaultdictfrom heapq import *def Prim (vertexs, edges, start_node ):list )for v1, v2, length in edges:set (start_node)while adjacent_vertexs_edges:if v2 not in closed:for next_vertex in adjacent_vertex[v2]:if next_vertex[2 ] not in closed:return mstlist ("ABCDEFG" )"A" , "B" , 7 ), ("A" , "D" , 5 ),"B" , "C" , 8 ), ("B" , "D" , 9 ), "B" , "E" , 7 ), ("C" , "E" , 5 ),"D" , "E" , 15 ), ("D" , "F" , 6 ),"E" , "F" , 8 ), ("E" , "G" , 9 ),"F" , "G" , 11 )]'prim:' , Prim(vertexs, edges, 'A' ))
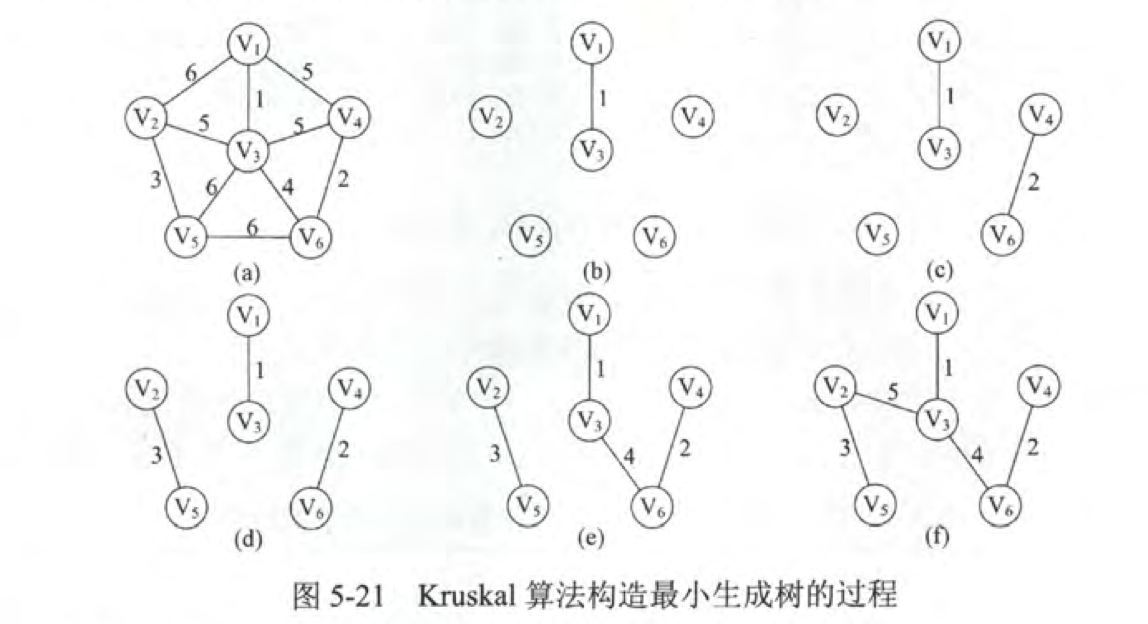
Kruskal算法
Kruskal是另一个计算最小生成树的算法,其算法原理如下。首先,将每个顶点放入其自身的数据集合中。然后,按照权值的升序来选择边。当选择每条边时,判断定义边的顶点是否在不同的数据集中。如果是,将此边插入最小生成树的集合中,同时,将集合中包含每个顶点的联合体取出,如果不是,就移动到下一条边。重复这个过程直到所有的边都探查过。适合边少点多的图。
1139760-20181009152448537-1374278496
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 node = dict () dict ()def make_set (point ):0 def find (point ):if node[point] != point:return node[point]def merge (point1, point2 ):if root1 != root2:if rank[root1] > rank[root2]:else :if rank[root1] == rank[root2]: 1 def Kruskal (graph ):for vertice in graph['vertices' ]:set ()list (graph['edges' ])for edge in edges:if find(v1) != find(v2):return mst'vertices' : ['A' , 'B' , 'C' , 'D' ],'edges' : set ([1 , 'A' , 'B' ),5 , 'A' , 'C' ),3 , 'A' , 'D' ),4 , 'B' , 'C' ),2 , 'B' , 'D' ),1 , 'C' , 'D' ),
一张图看懂数据结构——图
20200508105556140
参考连接
Python实现图的经典DFS、BFS、Dijkstra、Floyd、Prim、Kruskal算法 关于最小生成树 算法,推荐这个博客,讲的很清楚! 作者:卡巴拉的树 链接:https://www.jianshu.com/p/efcd21494dff 来源:简书 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。 一张图看懂数据结构 —— k图
堆
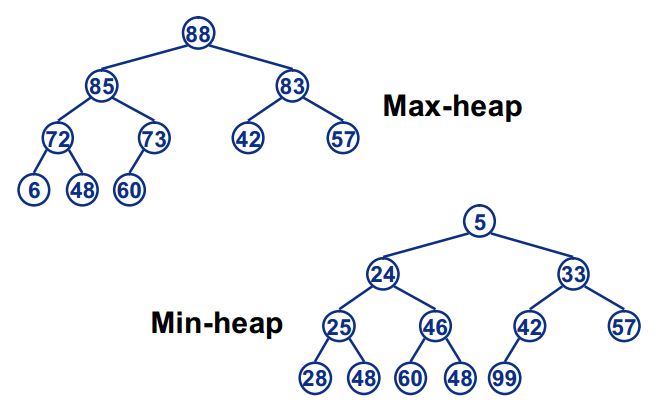
最大堆(大根堆)的定义:
最大堆中的最大元素值 出现在根结点(堆顶)
堆中每个父节点的元素值都大于等于 其孩子结点
最小堆(小根堆)的定义:
最大堆中的最小元素值 出现在根结点(堆顶)
堆中每个父节点的元素值都小于等于 其孩子结点
650075-91f1549ff0c87c15.png
时间复杂度:
大根堆获取最大值的操作,时间复杂度为 \(O(1)\) 。
堆的插入和删除操作,时间复杂度为 \(O(logN)\) ,\(N\) 是节点个数。
堆的基础操作
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 class heap (object def __init__ (self ):''' 初始化一个空堆,使用数组来在存放堆元素,节省存储 ''' def get_parent_index (self, index ):''' 返回父节点的下标 ''' if index == 0 or index > len (self.data_list) - 1 :return None else :return (index - 1 ) >> 1 def swap (self,index_a, index_b ):''' 交换数组中的两个元素 ''' def insert (self, data ):''' 先把元素放在最后,然后从后往前依次堆化 这里以大顶堆为例,如果插入元素比父节点大,则交换,直到最后 ''' len (self.data_list) - 1 while parent is not None and self.data_list[parent] < self.data_list[index]:def removeMax (self ):''' 删除堆顶元素,然后将最后一个元素放在堆顶,再从上往下依次堆化 ''' if len (self.data_list) > 0 :0 ]0 ] = self.data_list[-1 ]del self.data_list[-1 ]0 )return remove_dataelse :'堆空' )return None def heapify (self, index ):''' 从上往下堆化,从index 开始堆化操作 (大顶堆) ''' len (self.data_list) - 1 while True :if 2 *index + 1 <= total_index and self.data_list[2 *index + 1 ] > self.data_list[maxvalue_index]:2 *index + 1 if 2 *index + 2 <= total_index and self.data_list[2 *index + 2 ] > self.data_list[maxvalue_index]:2 *index + 2 if maxvalue_index == index:break def getMax (self ):""" 获取堆顶元素 """ if len (self.data_list) > 0 :return self.data_list[0 ]else :'堆空' )return None if __name__ == "__main__" :6 ]"输入数据:{}" .format (nums))"开始建堆" )for num in nums:"建堆完成:" , myheap.data_list)"获得堆顶元素:" , myheap.getMax())"当前的堆:" , myheap.data_list)"删除堆顶元素:" , myheap.removeMax())"删除之后的堆:" , myheap.data_list)"删除堆顶元素:" , myheap.removeMax())"删除之后的堆:" , myheap.data_list)
Python内建的Heap
Python 中 heapq 模块是小顶堆。实现 大顶堆 方法: 小顶堆的插入和弹出操作均将元素 取反 即可。通过把元素取反再放入堆,出堆时再取反, 把问题转换为最小堆问题也能间接实现最大堆
from heapq import *100 150
常用函数
heappush(heap, x)
将x压入堆中
heappop(heap)
从堆中弹出最小的元素
heapify(heap)
让列表具备堆特征
heapreplace(heap, x)
弹出最小的元素,并将x压入堆中
nlargest(n, iter)
返回iter中n个最大的元素
nsmallest(n, iter)
返回iter中n个最小的元素
堆排序
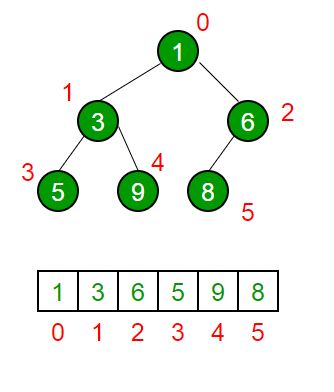
堆排序是一种基于二叉堆(Binary Heap)结构的排序算法,所谓二叉堆,就是一种特殊的完全二叉树,只不过相比较完全二叉树而言,二叉堆的所有父节点的值都大于(或者小于)它的孩子节点,像这样:
v2-5d6119c9801eadb83402ef68f6d4b689_720w.jpg
堆排序算法的内容就很简单了,最大堆堆顶的最大数取出,将剩余的堆继续调整为最大堆,再次将堆顶的最大数取出,这个过程持续到剩余数只有一个时结束。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 def heapSort (self, nums ):def swap (nums, i, j ):def heapify (nums, n, i ):2 * i + 1 2 * i + 2 if l < n and nums[l] > nums[largest]: if r < n and nums[r] > nums[largest]: if largest != i: len (nums)for i in range (_len // 2 - 1 , -1 , -1 ): for i in range (_len - 1 , -1 , -1 ): 0 )0 )return nums
参考链接
堆的实现及工程应用(Python) https://www.jb51.net/article/87552.htm