LeetCode 97. 交错字符串(难)
这道题,难在读懂题意,找到状态转移方程。
题目
给定三个字符串 s1, s2, s3, 验证 s3 是否是由 s1 和 s2 交错组成的。
动态规划
示例
示例 1:
1 | |
示例 2:
1 | |
考察知识点
动态规划、回溯算法
核心思想
方法一、动态规划算法
考虑用 s1 和 s2 的某个前缀是否能形成 s3 的一个前缀。
这个方法的前提建立于:判断一个 s3 的前缀(用下标 k 表示),能否用 s1 和 s2 的前缀(下标分别为 i 和 j),仅仅依赖于 s1 前 i 个字符和 s2 前 j 个字符,而与后面的字符无关。
为了实现这个算法, 我们将使用一个 2D 的布尔数组 dp 。dp[i][j] 表示用 s1 的前 (i+1) 和 s2 的前 (j+1) 个字符,总共 (i+j+2) 个字符,是否交错构成 s3 的前缀。为了求出 dp[i][j],我们需要考虑 2 种情况:
s1的第i个字符和s2的第j个字符都不能匹配s3的第k个字符,其中k=i+j+1。这种情况下,s1和s2的前缀无法交错形成s3长度为k+1的前缀。因此,我们让dp[i][j]为False。s1的第i个字符或者s2的第j个字符可以匹配s3的第k个字符,其中k=i+j+1。假设匹配的字符是x且与s1的第i个字符匹配,我们就需要把x放在已经形成的交错字符串的最后一个位置。此时,为了我们必须确保s1的前(i-1)个字符和s2的前j个字符能形成s3的一个前缀。类似的,如果我们将s2的第j个字符与s3的第k个字符匹配,我们需要确保s1的前i个字符和s2的前(j-1)个字符能形成s3的一个前缀,我们就让dp[i][j]为True。
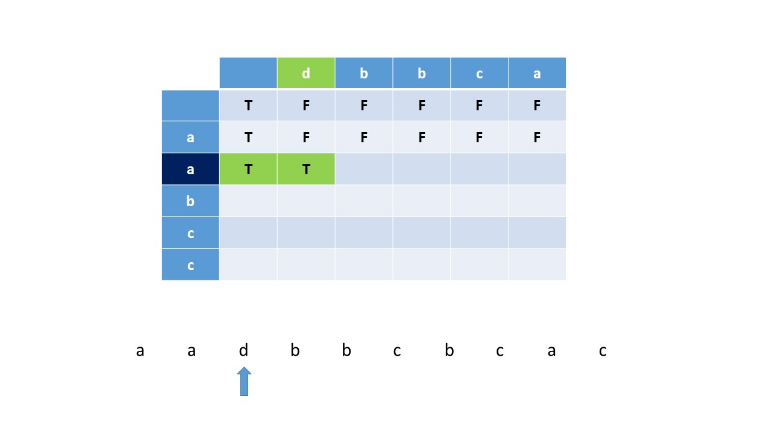
状态转换方程为(下图中i=1,j=0,dp[1][0] = True) \[
dp[i][j] = True\ if\ dp[i][j-1] = True\ and\ S_2(j) = S_3[j+i+1]
\]
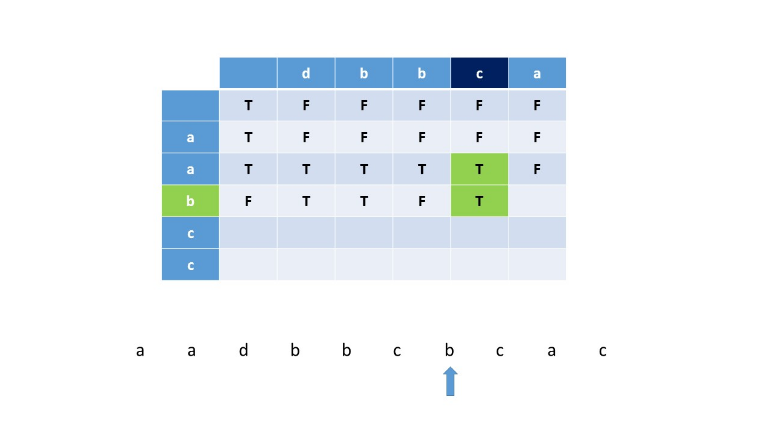
或(下图中i=2,j=3,dp[2][3] = True) \[
dp[i][j] = True\ if\ dp[i-1][j] = True\ and\ S_1(i) = S_3[j+i+1]
\]
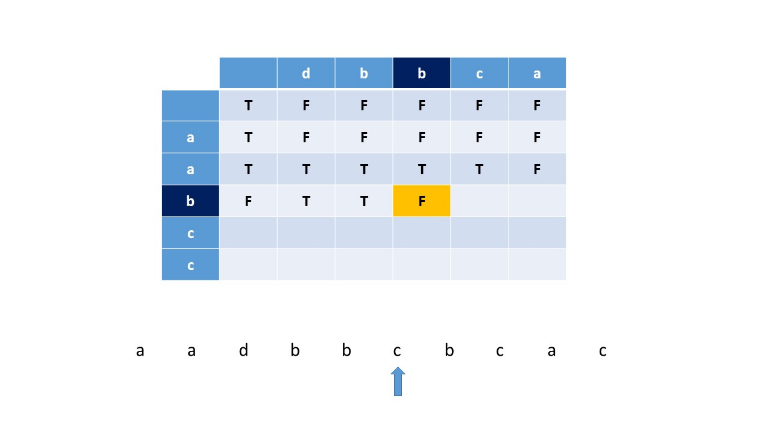
否则(下图中i=2,j=2,dp[2][2] = False)
\[ dp[i][j] = False \]
Python版本
方法一动态规划算法实现
1 | |
时间复杂度:\(O(m \times n)\) ,计算 dp 数组需要 \(m \times n\) 的时间。
空间复杂度:\(O(m \times n)\),2 维的 dp 数组需要 \((m+1) \times (n+1)\) 的空间。\(m\) 和 \(n\) 分别是 s1 和 s2 字符串的长度。
参考链接
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!