LeetCode 96. 不同的二叉搜索树（中）

一个披着二叉树外衣的动态规划问题

题目

给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

示例

示例:

1
2
3
4
5
6
7
8
9
10
输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

考察知识点

动态规划、数学（卡塔兰数）

核心思想

这是一个披着二叉树外衣的动态规划问题，实际上，这就是卡塔兰数的求解过程。
下图展示了状态转换的关系：

1.png
2.png

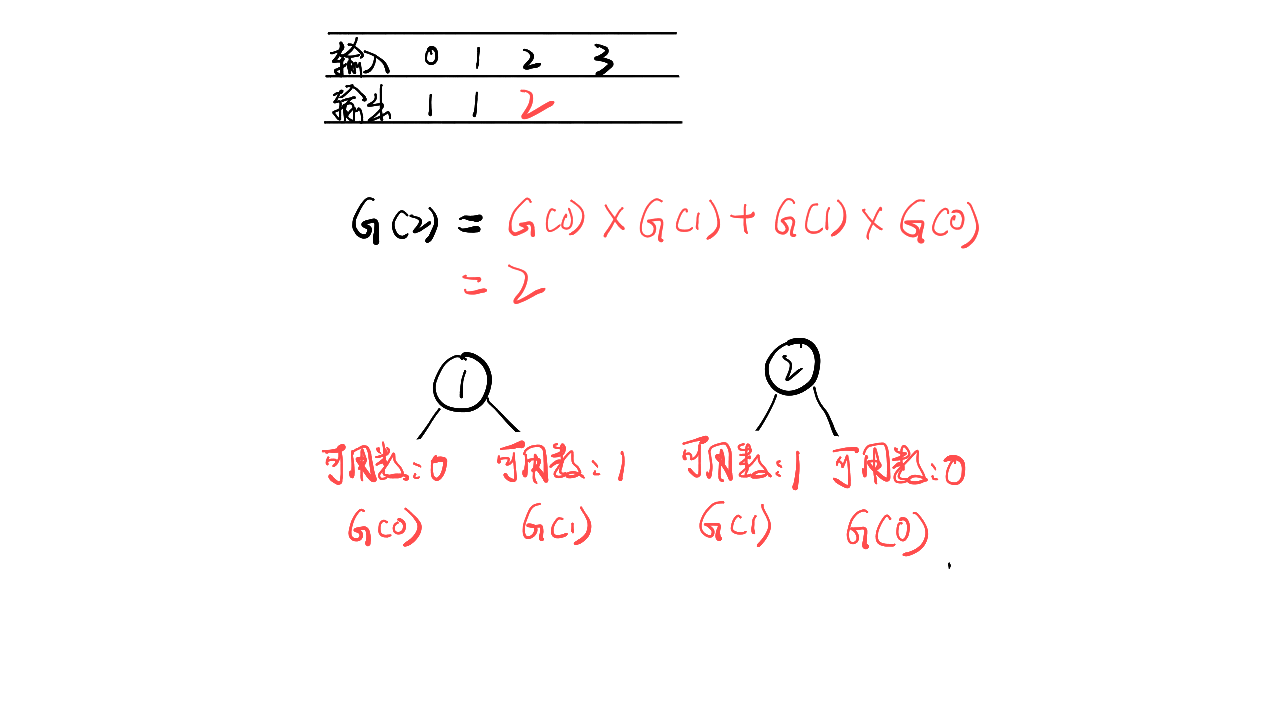
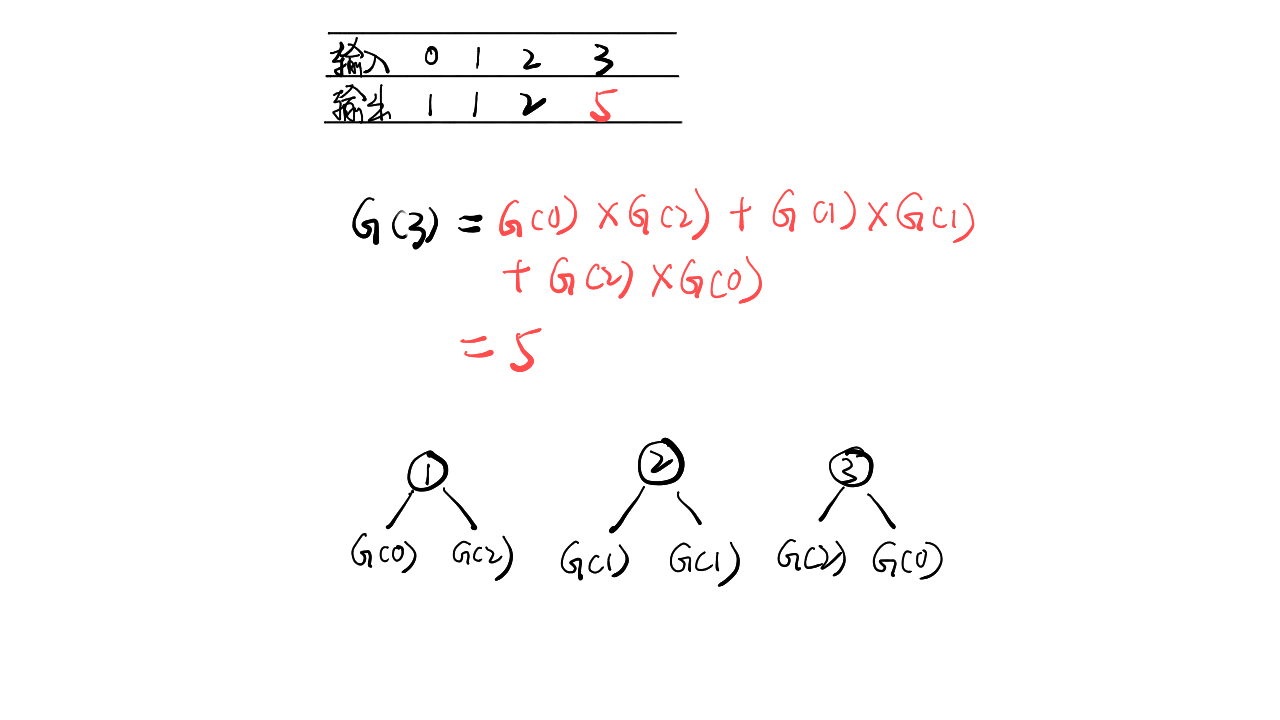
由上图可知状态转换方程为：
\[ dp[i] = dp[0]*dp[i-1] + dp[1]*dp[i-2] + ... + dp[i-2]*dp[1] + dp[i-1]*dp[0] \]

实际上就是卡塔兰数的求解方程，卡塔兰数是组合数学中一个常在各种计数问题中出现的数列。卡塔兰数的一般项公式为

公式

前20项的卡塔兰数为：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, ...

Python版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from typing import List

class Solution:
    def numTrees(self, n: int) -> int:
        dp = [1, 1] + [0] * (n - 1)
        i = 2
        while i <= n:
            j = 0
            while j < i:
                dp[i] += dp[j] * dp[i-j-1]
                j += 1
            i += 1
        return dp[-1]

Input = [3]
Answer = [5]
if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)): 
        print("-"*50)
        result = solution.numTrees(Input[i])
        print(result == Answer[i])

参考链接

!(Grandyang)[https://www.cnblogs.com/grandyang/p/4299608.html]