一道挺难的动态规划题目，dp矩阵达到了三维的规模。
关键是理解状态转换方程的推导。

\[ dp[i][j][k] = dp[j][j][w]\ and\ dp[i+w][j+w][k-w] (1 \leq w \leq k-1 ) \] OR
\[ dp[i][j][k] = dp[j][j+k-w][w]\ and\ dp[i+w][j][k-w] (1 \leq w \leq k-1 ) \]

题目

给定一个字符串 s1，我们可以把它递归地分割成两个非空子字符串，从而将其表示为二叉树。
下图是字符串 s1 = "great" 的一种可能的表示形式。

    great
   /    \
  gr    eat
 / \    /  \
g   r  e   at
           / \
          a   t

在扰乱这个字符串的过程中，我们可以挑选任何一个非叶节点，然后交换它的两个子节点。
例如，如果我们挑选非叶节点 "gr" ，交换它的两个子节点，将会产生扰乱字符串 "rgeat" 。

    rgeat
   /    \
  rg    eat
 / \    /  \
r   g  e   at
           / \
          a   t

我们将 "rgeat” 称作 "great" 的一个扰乱字符串。
同样地，如果我们继续交换节点 "eat" 和 "at" 的子节点，将会产生另一个新的扰乱字符串 "rgtae" 。

    rgtae
   /    \
  rg    tae
 / \    /  \
r   g  ta  e
       / \
      t   a

我们将 "rgtae” 称作 "great" 的一个扰乱字符串。
给出两个长度相等的字符串 s1 和 s2，判断 s2 是否是 s1 的扰乱字符串。

示例

示例 1:

1 2	`输入: s1 = "great", s2 = "rgeat" 输出: true`

示例 2:

1 2	`输入: s1 = "abcde", s2 = "caebd" 输出: false`

考察知识点

递归、动态规划

核心思想

方法一、递归
S 和 T 如果是扰动的话，那么必然存在一个在 S 上的长度 l1，将 S 分成 S1 和 S2 两段，同样 T 上也有一个长度l2，把 T 分为 T1 和 T2。
1、那么要么 S1 和 T1 是扰动的且 S2 和 T2 是扰动的，即字符串未交换。
2、要么 S1 和 T2 是扰动的且 S2 和 T1 是扰动的，即字符串交换了。
就拿题目中的例子 rgeat 和 great 来说，rgeat 可分成 rg 和 eat 两段， great 可分成 gr 和 eat 两段，rg 和gr是扰动的， eat和eat也是扰动的。

方法二、动态规划
直觉
给定两个字符串 \(T\) 和 \(S\)，假设 \(T\) 是由 \(S\) 变换而来。

如果 \(T\) 和 \(S\) 长度不一样，必定不能变来。
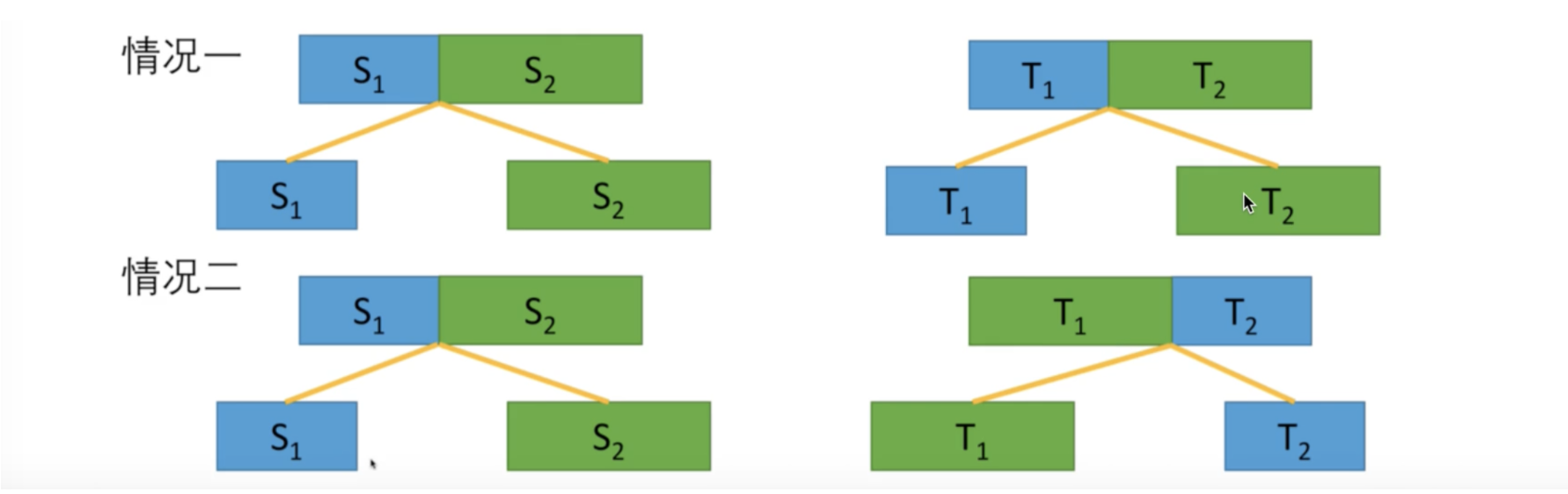
如果长度一样，顶层字符串 \(S\) 能够划分为 \(S_1\) 和 \(S_2\)，同理，字符串\(T\)也可以划分为 \(T_1\) 和 \(T_2\)。
- 情况一：没交换，\(S_1 = T_1\) 且 \(S_2 = T_2\)。
- 情况二：交换了，\(S_1 = T_2\) 且 \(S_2 = T_1\)。
子问题就是分别讨论两种情况，\(T_1\) 是否由 \(S_1\) 变来且\(T_2\) 是否由 \(S_2\) 变来。或者，\(T_1\) 是否由 \(S_2\) 变来且\(T_2\)是否由\(S_1\) 变来。

8358f1da723d09be915a17570d13e05d1b0b105839b751763429dcb876ce452d-image.png

状态
\(dp[i][j][k][h]\) 表示 \(T[k...h]\) 是否由 \(S[i...j]\) 变来。由于变换必须长度一样，所以上述变换关系可以从四维简化为三维，即，\(dp[i][j][len]\) 表示从字符串 \(S\) 中 \(i\) 开始长度为 \(len\) 的字符串是否能变换为从字符串 \(T\) 中 \(j\) 开始长度为 \(len\) 的字符串，因此转换方程如下：
\[ dp[i][j][k] = dp[j][j][w]\ and\ dp[i+w][j+w][k-w] (1 \leq w \leq k-1 )\ \ OR\ \ \\ dp[i][j][k] = dp[j][j+k-w][w]\ and\ dp[i+w][j][k-w] (1 \leq w \leq k-1 ) \]

解释下：枚举 \(S_1\)长度 \(w\)（从\(1～k-1\)，因为要划分），\(f[i][j][w]\) 表示 \(S_1\) 能变成 \(T_1\)，\(f[i+w][j+w][k-w]\)表示 \(S_2\) 可以变成 \(T_1\)。而 \(f[j][j+k-w][w]\) 表示 \(S_1\) 能变成 \(T_2\)，\(f[i+w][j][k-w]\) 表示 \(S_2\) 能变成 \(T_1\)。

初始条件
对于长度是1的子串，只有相等才能变过去，相等为 true，不相等为 false。

终止条件
\(dp[i][j][len]\) 表示字符串\(S\)从\(i\)开始长度为\(len\)的子串能否变换成字符串\(T\)从\(j\)开始长度为\(len\)的子串，所以终止条件为 \(dp[0][0][n] = True\)，其中 \(n\) 为输入字符串的长度。

算法

特判 S 和 T 长度不一样的情况
初始化三维数组 dp
初始化单个字符的情况。如果把 dp 三维数组想象成一个立方体，初始化单个字符的操作，就是设置w=1 然后初始化 i和j 组成的平面，也就是立方体的最底面。
开始划分区间，区间长度为n，也就是划分为 s1[:k] 和 s1[k:]，枚举区间长度2～n（n为字符串长度）
- 枚举S中的起点位置 i，也就是在 S 中枚举i的位置，因为后面会出现 i+w 的情况，而 w 最大就是 k，就会有 i+k 的情况，所以 i 的取值范围就是 0~n-k。
- 枚举 T 中的起点位置 j，同上，j 的取值范围就是 0~n-k。
- 枚举划分位置 w，范围是 1~k。
  - 第一种情况：S1->T1, S2->T2，当前层的两个子串未经过交换的情况。
  - 第二种情况：S1->T2, S2->T1，当前层的两个子串经过交换的情况。
返回 dp[0][0][n]

两种情况的判定的代码

图解

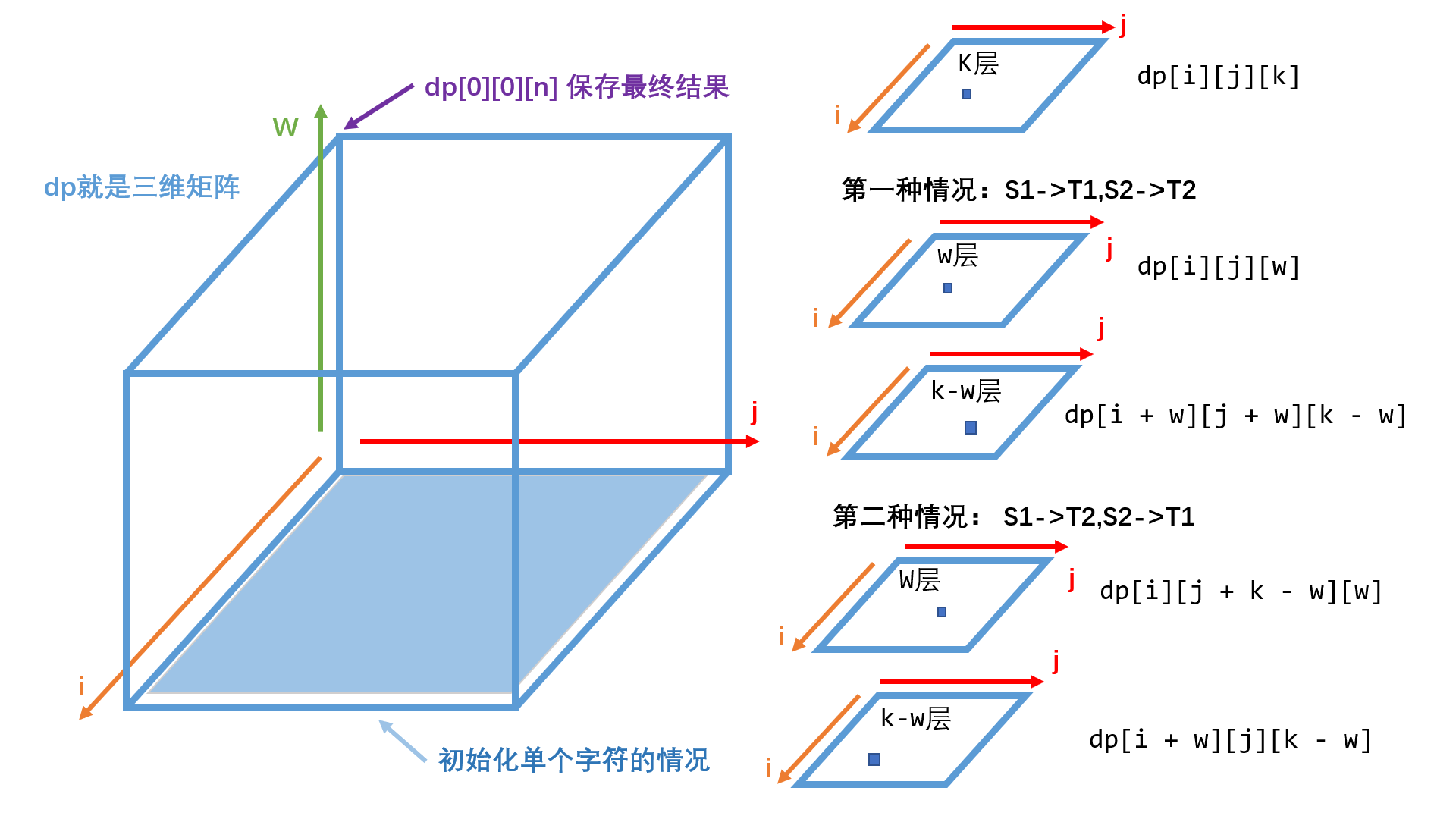
从这张图就可以知道动态规划的自底向上特性了。

Python版本

方法一递归的实现

import functools
class Solution:
    @functools.lru_cache(None)
    def isScramble(self, s1: str, s2: str) -> bool:
        if s1 == s2:
            return True
        if sorted(s1) != sorted(s2):
            return False
        for i in range(1, len(s1)):
            if self.isScramble(s1[:i],s2[:i]) and self.isScramble(s1[i:],s2[i:]):
                return True
            if self.isScramble(s1[:i],s2[-i:]) and self.isScramble(s1[i:],s2[:-i]):
                return True
        return False

简单的递归加上Python3自带的缓存机制 @functools.lru_cache(None)，以可以提高效率。
执行用时 :36 ms, 在所有 Python3 提交中击败了96.29%的用户
内存消耗 :13.5 MB, 在所有 Python3 提交中击败了21.88%的用户
实际上，递归的时间复杂度要大于动态规划，但是测试样例不存在 \(n!\) 的情况，所以效果还行。

方法二动态规划的实现

class Solution:
    def isScramble(self, s1, s2):
        S_len = len(s1)
        T_len = len(s2)
        
        # 一些特判
        if S_len != T_len:  return False
        if s1 == s2:  return True
        if sorted(s1) != sorted(s2):  return False
        
        # 初始化 dp 3维数组dp[i][j][k]
        # i为0~S_len共S_len+1个， j为0~S_len-1共S_len个， k为1~S_len+1共S_len个
        dp = [ [ [False]*(S_len+1) for _ in range(S_len) ] for _ in range(S_len) ]

        # 初始化单个字符的情况
        for i in range(S_len):
            for j in range(T_len):
                dp[i][j][1] = s1[i] == s2[j]  
        
        # 前面排除了s1和s2为单个字符的情况，那么我们就要划分区间了，k从2到S_len，也就是划分为s1[:k]和s1[k:]
        for k in range(2, S_len + 1):  # 枚举区间长度2～S_len
            # 枚举S中的起点位置 i，也就是在s1中枚举i的位置，因为后面会出现i+w的情况，而w最大就是k，就会有i+k的情况，所以i的取值范围就是0~S_len-k。
            for i in range(S_len - k + 1):
                # 枚举T中的起点位置 j
                for j in range(T_len - k + 1):
                    # 枚举划分位置 w
                    for w in range(1, k):
                        # 第一种情况：S1->T1,S2->T2，没有交换过。
                        if dp[i][j][w] and dp[i + w][j + w][k - w]:
                            dp[i][j][k] = True
                            break
                        # 第二种情况：S1->T2,S2->T1，发生了交换。
                        # S1起点i，T2起点j + 前面那段长度 k-w，S2起点i+前面长度w，T1起点为j。
                        if dp[i][j + k - w][w] and dp[i + w][j][k - w]:
                            dp[i][j][k] = True
                            break
        return dp[0][0][S_len]


Input = ["great", "abcde"]
Input1 = ["rgeat", "caebd"]
Answer = [True, False]
if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)): 
        print("-"*50)
        reslut = solution.isScramble(Input[i], Input1[i])
        print(reslut == Answer[i])

执行用时 :276 ms, 在所有 Python3 提交中击败了25.00%的用户
内存消耗 :13.8 MB, 在所有 Python3 提交中击败了17.19%的用户

有效语法糖

1、Python 缓存机制与 functools.lru_cache

缓存是一种将定量数据加以保存以备迎合后续获取需求的处理方式，旨在加快数据获取的速度。数据的生成过程可能需要经过计算，规整，远程获取等操作，如果是同一份数据需要多次使用，每次都重新生成会大大浪费时间。所以，如果将计算或者远程请求等操作获得的数据缓存下来，会加快后续的数据获取需求。

>>> from functools import lru_cache
>>> @lru_cache(None)
... def add(x, y):
...     print("calculating: %s + %s" % (x, y))
...     return x + y
...
>>> print(add(1, 2))
calculating: 1 + 2
3
>>> print(add(1, 2))
3
>>> print(add(2, 3))
calculating: 2 + 3
5

从结果可以看出，当第二次调用 add(1, 2) 时，并没有真正执行函数体，而是直接返回缓存的结果。

参考链接

力扣（LeetCode）powcai
力扣（LeetCode）jerry_njuT_1
Python 缓存机制与 functools.lru_cache

LeetCode

动态规划

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

LeetCode 88. 合并两个有序数组（易）上一篇

LeetCode 86. 分隔链表（中）下一篇

LeetCode 87. 扰乱字符串（难）

题目

示例

考察知识点

核心思想

Python版本

有效语法糖