LeetCode 84. 柱状图中最大的矩形

和 11. 盛最多水的容器 类似，使用栈记录遍历的下标，计算最大面积。
关键是清楚计算触发的位置在局部峰值处。
只要当前的数字大于后面的一个数字，那么当前数字就看作一个局部峰值，跟前面的数字大小无关。

题目

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

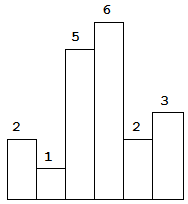
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2, 1, 5, 6, 2, 3]。

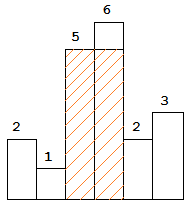
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例

示例:

1
2
输入: [2,1,5,6,2,3]
输出: 10

考察知识点

栈、数组、单调栈

核心思想

方法一、基于局部峰值的方法（贪心算法）
一个很好的优化方法，就是遍历数组，每找到一个局部峰值（只要当前的数字大于后面的一个数字，那么当前数字就看作一个局部峰值，跟前面的数字大小无关），然后向前遍历所有的值，算出共同的矩形面积，每次对比保留最大值。这里再说下为啥要从局部峰值处理，看题目中的例子，局部峰值为 2(2>1)，6(6>2)，3(3>2)，我们只需在这些局部峰值出进行处理，为啥不用在非局部峰值处统计呢，这是因为非局部峰值处的情况，后面的局部峰值都可以包括，比如1和5，由于局部峰值6是高于1和5的，所有1和5能组成的矩形，到6这里都能组成，并且还可以加上6本身的一部分组成更大的矩形，那么就不用费力气去再统计一个1和5处能组成的矩形了。

方法二、基单调于栈的方法

什么是单调栈？

单调栈分为单调递增栈和单调递减栈 1、单调递增栈即栈内元素保持单调递增的栈 2、同理单调递减栈即栈内元素保持单调递减的栈

操作规则（下面都以单调递增栈为例） 1、如果新的元素比栈顶元素大，就入栈。 2、如果新的元素较小，那就一直把栈内元素弹出来，直到栈顶比新元素小

加入这样一个规则之后，会有什么效果 1、栈内的元素是递增的 2、当元素出栈时，说明这个新元素是出栈元素向后找第一个比其小的元素

本题思路

维护一个栈，用来保存递增序列，相当于上面那种方法的找局部峰值。
我们可以看到，直方图矩形面积要最大的话，需要尽可能的使得连续的矩形多，并且最低一块的高度要高。
那么既然需要用单调栈来做，首先要考虑到底用递增栈（栈内的元素，从栈底到栈顶，依次增大），还是用递减栈（栈内的元素，从栈底到栈顶，依次减小）来做。
递增栈是维护递增的顺序，当遇到小于栈顶元素的数就开始处理，而递减栈正好相反，维护递减的顺序，当遇到大于栈顶元素的数开始处理。
那么根据这道题的特点，我们需要按从高板子到低板子的顺序处理，先处理最高的板子，宽度为1，然后再处理旁边矮一些的板子，此时长度为2，因为之前的高板子可组成矮板子的矩形 ，因此我们需要一个递增栈，当遇到大的数字直接进栈，而当遇到小于栈顶元素的数字时，就要取出栈顶元素进行处理了，那取出的顺序就是从高板子到矮板子了（且栈是从栈顶取数字，所以越到栈顶，数字越大才能保证取出顺序是从大到小，因此栈内从栈底到栈顶，数字依次递增，所以该栈是一个递增栈），也就是说，遇到的较小的数字才触发，需要开始计算矩形面积了
为了使得最后一块板子也被处理，这里用了个小 trick，在高度数组 heights 最后面加上一个0，这样原先的最后一个板子也可以被处理了。
由于栈顶元素是矩形的高度，那么关键就是求出来宽度，那么跟之前那道 Trapping Rain Water 一样，单调栈中不能放高度，而是需要放坐标。
由于我们先取出栈中最高的板子，那么就可以先算出长度为1的矩形面积了，然后再取下一个板子，此时根据矮板子的高度算长度为2的矩形面积，以此类推，直到数字大于栈顶元素为止，再次进栈，巧妙的一比。

参考链接：力扣（LeetCode）ikaruga 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

Python版本

  • 方法一的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from typing import List


class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        res = 0
        i = 0
        while i < len(heights):
            if i + 1 < len(heights) and heights[i] <= heights[i+1]:
                i += 1
            else:  # 局部峰值
                minH = heights[i]
                j = i  # 设置 j = i 从局部峰值出现的地方往前推导计算area，知道第一个条块。
                while j >= 0:
                    minH = min(minH, heights[j])
                    area = minH * (i - j + 1)
                    res = max(res, area)
                    j -= 1
                i += 1

        return res


Input = [[2,1,5,6,2,3]]
Answer = [10]

if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)): 
        print("-"*50)
        reslut = solution.largestRectangleArea(Input[i])
        print(reslut == Answer[i])

时间复杂度：\(O(n^2)\)， 需要枚举所有可能的柱子对。
空间复杂度：\(O(1)\)，不需要额外的空间。

  • 方法二的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        res = 0
        st = []
        heights.append(0)
        i = 0
        while i < len(heights):
            if not len(st) or heights[st[-1]] < heights[i]:  # 当遇到更高的条块时就入栈
                st.append(i)
            else:  # heights[st[-1]] >= heights[i]，否则就是遇到了下降，也就是局部峰值后面的那个条块。
                cur = st.pop()  # 弹出栈顶，也就是局部峰值那个条块的下标。
                width = i if not len(st) else (i - st[-1] - 1)
                res = max(res, heights[cur] * width)
                i -= 1  # 这个减一很关键，将i回退到了局部峰值的位置，下一次遍历i又会变到局部峰值后面的那个条块对应的那个下标。
            i += 1

        return res

时间复杂度：\(O(n)\)。 \(n\) 个数字每个会被压栈弹栈各一次。
空间复杂度： \(O(n)\)。用来存放栈中元素。

参考链接

Grandyang

C++版本

  • 方法二的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<iostream>
#include <vector>
using namespace std;

class Solution {
    public:
        int largestRectangleArea(vector<int>& heights) {
            int res = 0;
            vector<int> stack;
            heights.insert(heights.begin(), 0);  // heights.appedn(0) 在 heights 的末尾加入 0 作为初始值
            heights.push_back(0);
            for(int i = 0; i < heights.size(); i++){
                while(!stack.empty() && heights[stack.back()] > heights[i]){  // heights[st[-1]] > heights[i]，否则就是遇到了下降，也就是局部峰值后面的那个条块。
                    int cur = stack.back();  // 弹出栈顶，也就是局部峰值那个条块的下标。
                    stack.pop_back();
                    int left = stack.back() + 1;
                    int right = i - 1;
                    res = max(res, (right - left + 1) * heights[cur]);
                }
                // 当遇到更高的条块时就入栈
                stack.push_back(i);
            }
            return res;
        }
};

int main(){
    Solution solve;
    vector<int> input = {2, 1, 5, 6, 2, 3};
    cout << solve.largestRectangleArea(input) << endl;
    system("pause");
    return 0;
}