78题改进，出现了重复数字，需要添加限制条件。
之前一直在for架构下，在选择之前想办法做判断。
试了很多次都不成功，原来要修改的地方在“退出回溯撤销选择”之后。

题目

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
说明：解集不能包含重复的子集。

示例

示例:

输入: [1,2,2]

输出:
[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

考察知识点

回溯、数组

核心思想

这道题和 Leecode 第78题子集差不多一样，区别是本题出现了重复数字，且结果不允许重复。78题的解题方法包括递归回溯、循环迭代、状态分配（基于字典、矩阵、位运算）三种方法。本题在78题代码的基础上添加某些限制条件即可。

方法一、递归回溯

相较于78题的区别是：
1、在调用 backtrack() 之前先将 nums 数组排序
2、当退出回溯函数 backtrack 并撤销选择 path.pop() 之后，判断后面是否有相同的数字，如果有，就跳过。

78题代码

for i in range(start, n - (k - cur_len) + 1):
    path.append(nums[i])  # 选择
    backtrack(i + 1, path)  # 回溯
    path.pop()  # 退出回溯 撤销选择

90题代码

# 在调用 backtrack() 之前先将nums数组排序
nums.sort()
i = first
while i < n - (k - path_len) + 1:  # 改成while循环
    path.append(nums[i])  # 选择
    backtrack(i + 1, path, last)  # 回溯
    path.pop()  # 退出回溯 撤销选择
    while i + 1 < len(nums) and nums[i] == nums[i+1]:  # 添加的部分限制条件，如果当前位置后面有相同数字，就跳过。
        i += 1
    i += 1

总结：之前一直在for架构下，在选择之前想办法做判断，试了很多次都不成功，原来要修改的地方在“退出回溯撤销选择”之后。

方法二、循环迭代

相较于78题的区别是：

1、循环开始前先对 nums 进行排序
2、判断当前数字和前一个数字是否相似
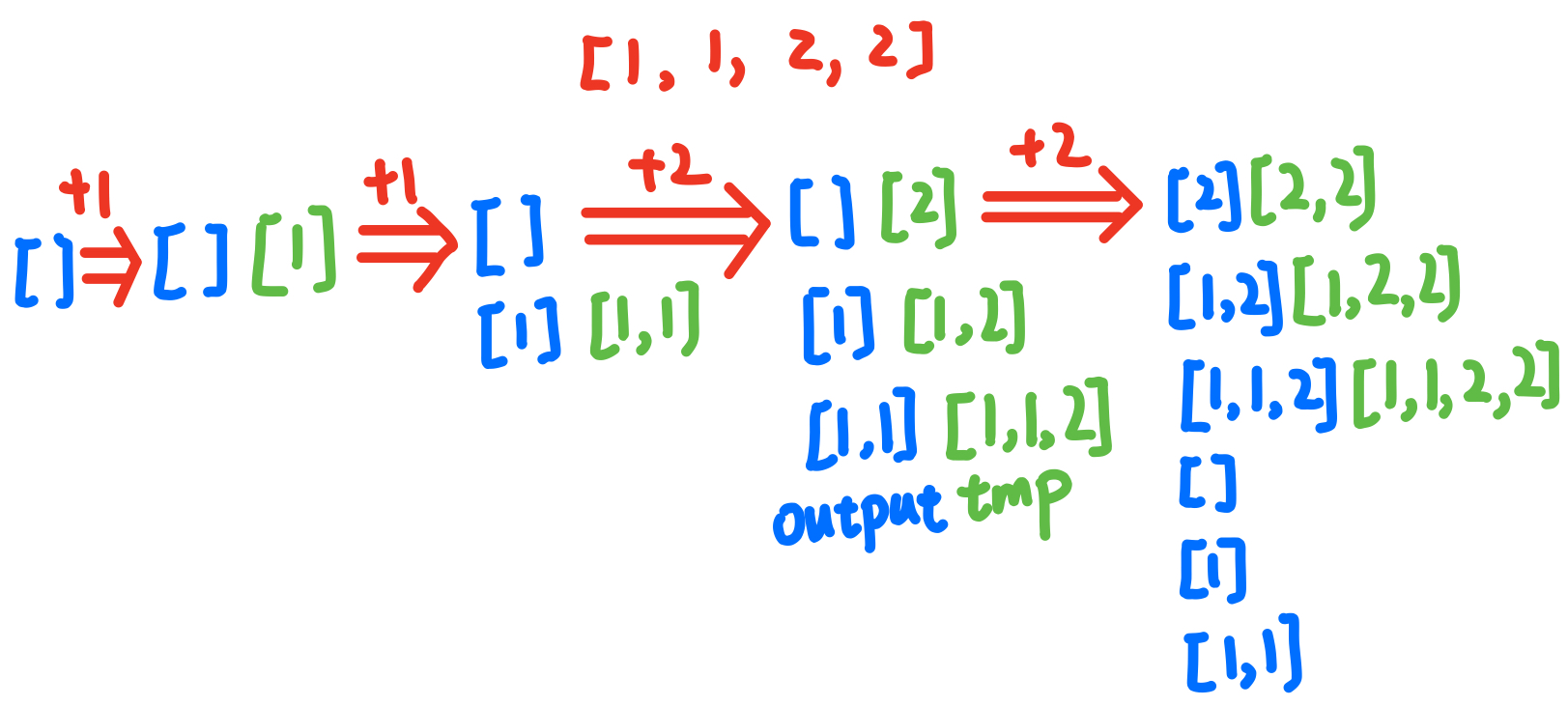
2.1、如果和前一个数字一样，就在前一次循环产生的增量数组 tmp 上添加。
2.2、如果和前一个数字不一样，就在前一次循环产生的结果 output 上添加。

78题代码

1
2
3

for num in nums:
    output += [curr + [num] for curr in output]
    return output

90题代码

# 循环开始前先对nums进行排序
nums.sort()
tmp = []
for i in range(len(nums)):
    if i > 0 and nums[i - 1] == nums[i]:  
        tmp = [curr + [nums[i]] for curr in tmp]
    else:
        tmp = [curr + [nums[i]] for curr in output]
    output += tmp
return output

方法三、状态分配（字典排序（二进制排序）子集）

暂无

Python版本

方法一递归回溯的实现

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        def backtrack(first = 0, path = [], last=[]):
            path_len = len(path)
            if path_len == k:
                output.append(path[:])
                return
            i = first
            while i < n - (k - path_len) + 1:
                path.append(nums[i])
                backtrack(i + 1, path, last)
                path.pop()
                while i + 1 < len(nums) and nums[i] == nums[i+1]:
                    i += 1
                i += 1

        nums.sort()
        output = []
        n = len(nums)
        for k in range(n + 1):
            backtrack()
        return output


Input = [[1,1,2,2], [1,2,2]]
Answer = [
    [[],[1],[2],[1,1],[1,2],[2,2],[1,1,2],[1,2,2],[1,1,2,2],],
    [[], [1], [2], [1, 2], [2, 2], [1, 2, 2]]
]

if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)): 
        print("-"*50)
        reslut = solution.subsetsWithDup(Input[i])
        if reslut == Answer[i]:
            print(True)
        else:
            print(False)
            print(reslut)
            print(Answer[i])

时间复杂度：\(O(N \times 2^N)\)，考虑最坏的情况，不存在任何重复，就和78题一样了。
空间复杂度：\(O(N \times 2^N)\)，同上，考虑最坏的情况，不存在任何重复，就和78题一样了。
执行用时 :48 ms, 在所有 Python3 提交中击败了42.99%的用户
内存消耗 :13.6 MB, 在所有 Python3 提交中击败了5.83%的用户

另一种简单回溯的写法

class Solution(object):
    def subsetsWithDup(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        if not nums:
            return []
        n = len(nums)
        res = []
        nums.sort()
        # 思路1
        def backtrack1(idx, n, temp_list):
            if temp_list not in res:  # 此处去重
                res.append(temp_list)
            for i in range(idx, n):
                backtrack1(i + 1, n, temp_list + [nums[i]])
        # 思路2
        def backtrack2(idx, n, temp_list):
            res.append(temp_list)
            for i in range(idx, n):
                if i > idx and  nums[i] == nums[i - 1]:  # 此处去重
                    continue
                backtrack2(i + 1, n, temp_list + [nums[i]])

        helper2(0, n, [])
        return res

时间复杂度：\(O(N \times 2^N)\)
空间复杂度：\(O(N \times 2^N)\)
执行用时 :32 ms, 在所有 Python3 提交中击败了97.05%的用户
内存消耗 :13.5 MB, 在所有 Python3 提交中击败了5.83%的用户

方法二循环迭代的实现

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        if not nums: return []
        output = [[]]
        nums.sort()
        tmp = []
        for i in range(len(nums)):
            if i > 0 and nums[i - 1] == nums[i]:  # 如果和前一个数字一样
                tmp = [curr + [nums[i]] for curr in tmp]  # 就在前一次循环产生的增量数组 tmp 上添加。
            else:  # 如果和前一个数字不一样
                tmp = [curr + [nums[i]] for curr in output]  # 就在前一次循环产生的结果 output 上添加
            output += tmp
        return output

时间复杂度：\(O(N \times 2^N)\) ，生成所有子集，并复制到输出结果中。
空间复杂度：\(O(N \times 2^N)\) ，这是子集的数量。
执行用时 :40 ms, 在所有 Python3 提交中击败了74.98%的用户
内存消耗 :13.6 MB, 在所有 Python3 提交中击败了5.83%的用户