经典问题，从常规解到剪枝优化再到非回溯解法进行了记录，需要特别关注。

题目

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例

示例:

# 输入
n = 4, k = 2
# 输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

考察知识点

回溯算法

核心思想

方法一、回溯法
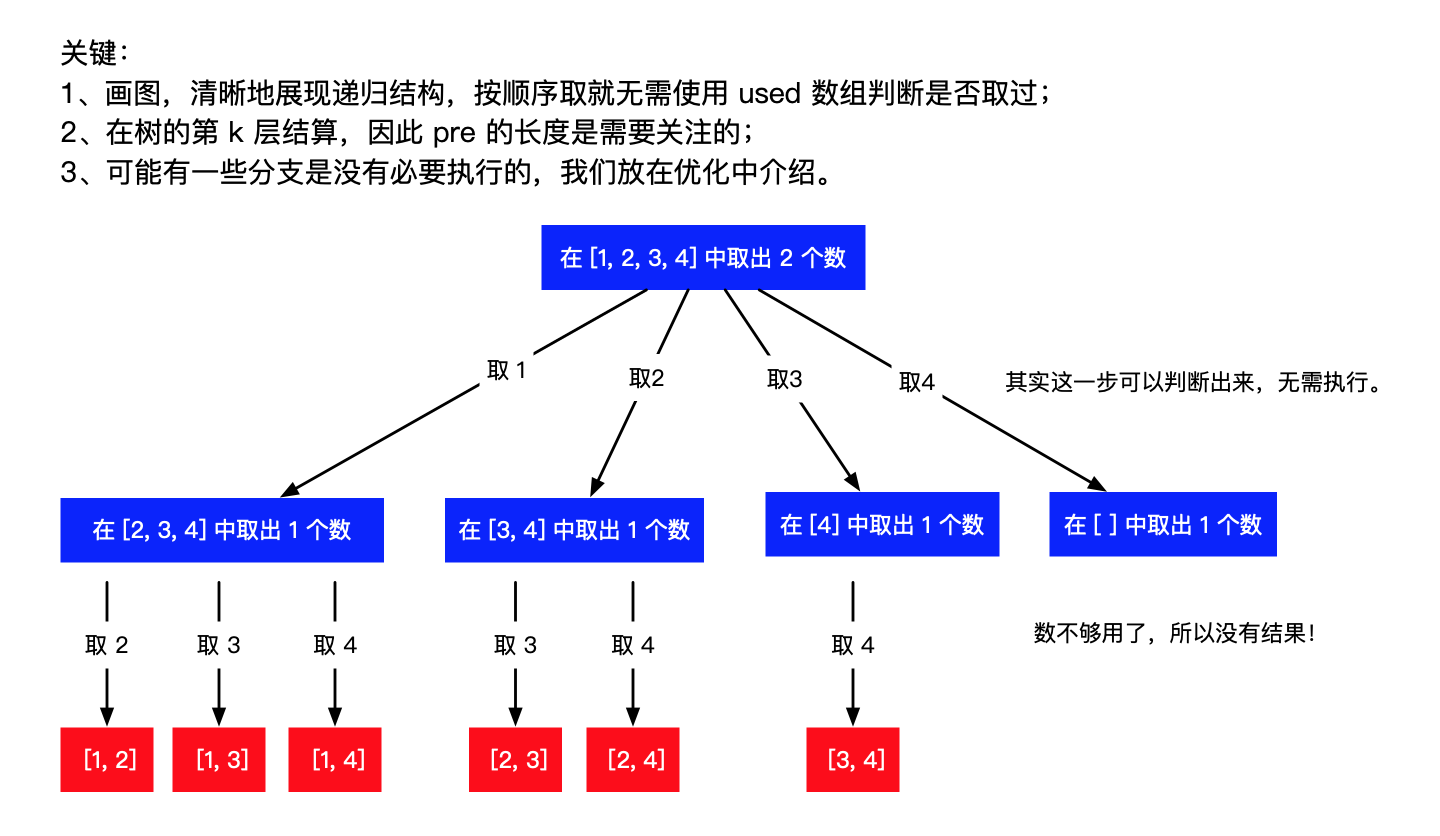
不设置 is_validate 函数和 used 变量，每次都从下一个位置开始遍历，这样就跳过了重复的情况。例如，取了1，从[2, 3, 4]中匹配，跳过了1本身，避免了 [1, 1] 这样的答案。输出 [1, 2]、[1, 3] 、[1, 4] 三种情况之后，再取2，就要从[3, 4]中匹配，跳过了1和2，避免了[2, 1]、[2, 2] 这样的答案。

fcdaa96defd9caacec12eb6c86cac6b8932c93d7a6da7a649791e1031a8da2b5-image.png

方法二、回溯加剪枝

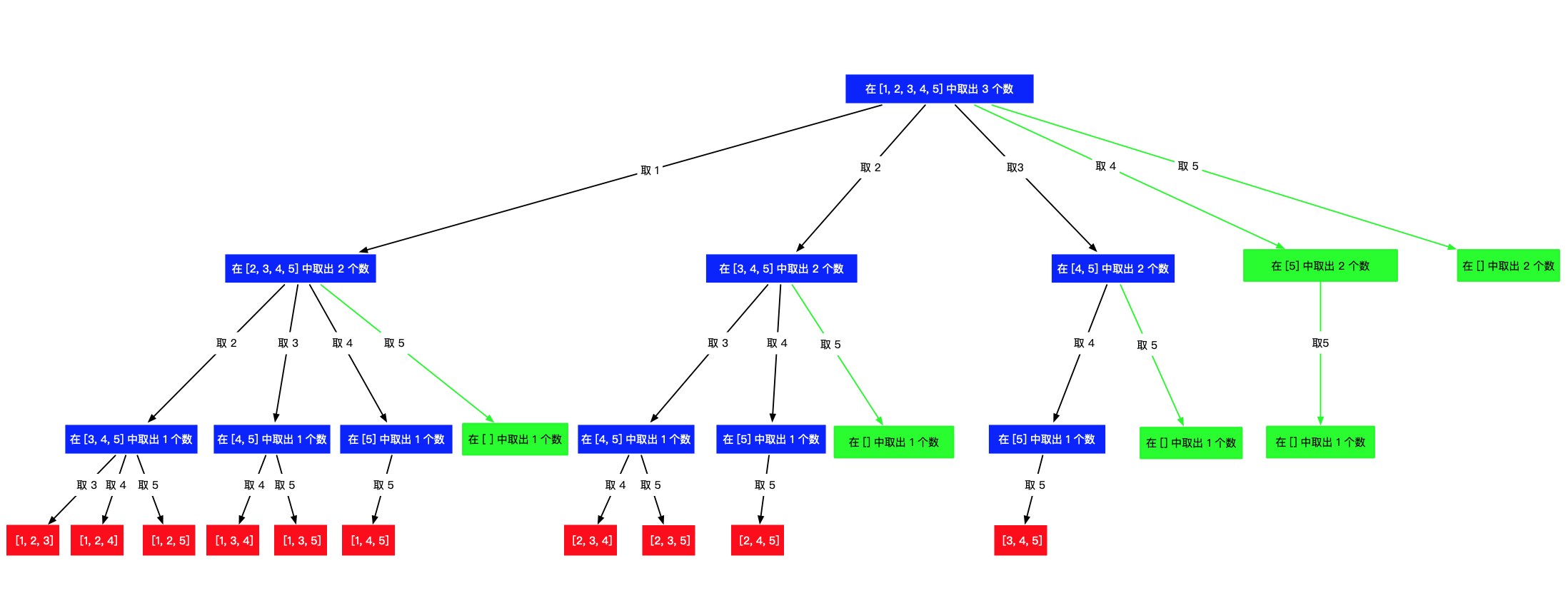
其中绿色的部分，是不能产生结果的分支，但是我们的代码确实又执行到了这部分。
上面的代码中，我们发现：其实如果 pre 已经选择到 [1,4,5] 或者 [2,4,5] 或者 [3,4,5] ，后序的代码就没有必要执行，继续走也不能发现新的满足题意的组合。[1,4,5]之后的多余步骤如下：
1、选择了 [1,4,5] 以后， 5 弹出 [1,4,5] 成为 [1,4]
2、4 弹出 [1,4] 成为 [1] ，然后 5 进来，成为 [1,5]。
3、再继续循环，会发现 for 循环都进不了（因为没有可选的元素），然后 5 又弹出，接着 1 弹出。
以上几步其实都是多余步骤。

3ddd55697423b5831cbbd42f4b901ebbade0daa456c651a70c758fe359d8a0d1-image.png

发现多余操作：那么我们如何发现多余的步骤呢，其实也是有规律可寻的，就在 for 循环中：

for i in range(first, n+1):
    pre.append(i)
    backtrack(i + 1, selects)
    pre.pop()

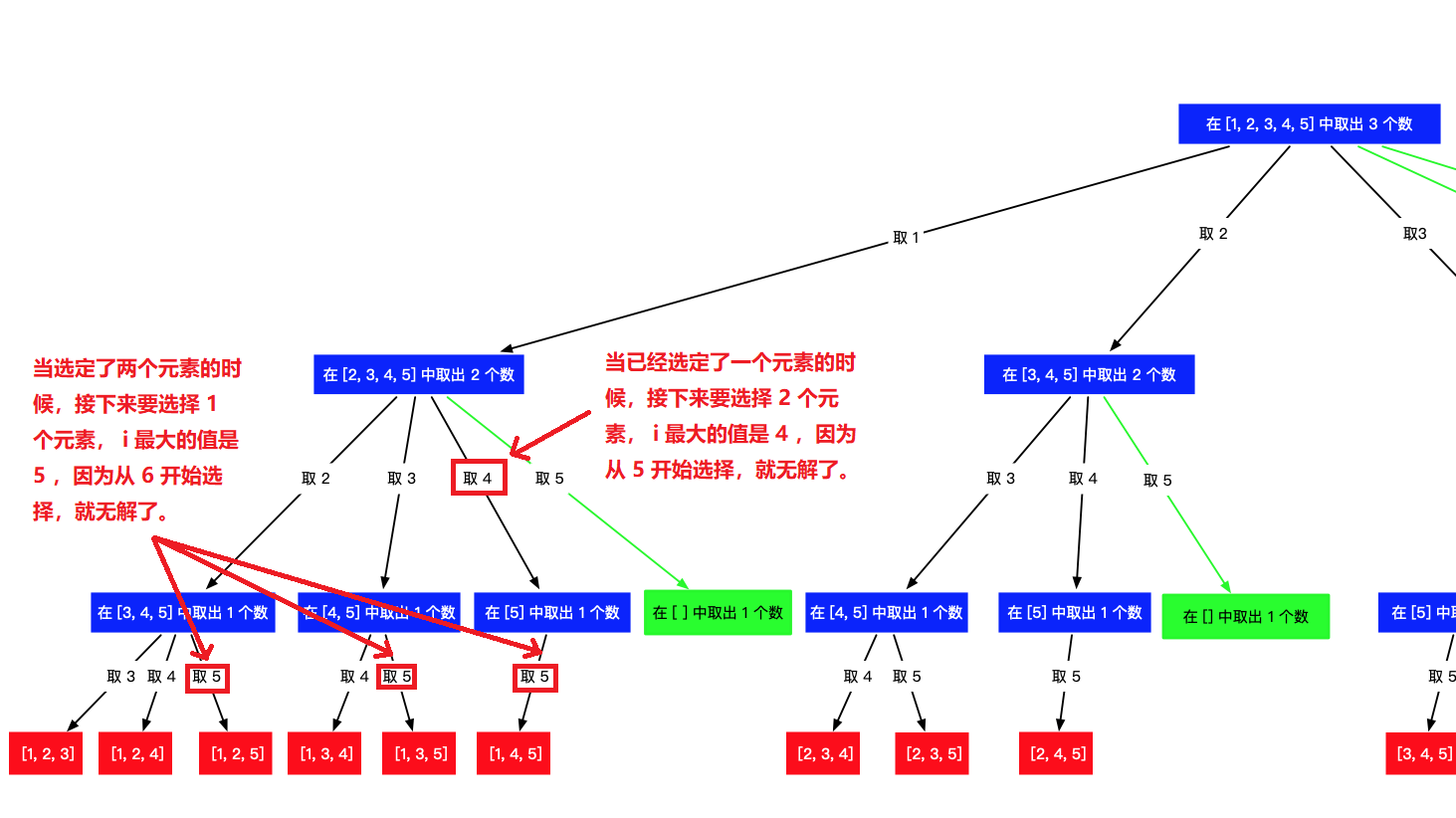
这个for循环干的事情，是从 [i, n] 这个区间里（注意，左右都是闭区间），找到 k - len(selects)个元素。 i 不是每一次都要走到 n 的， i 有一个上限。那这个上限是多少呢？通过观察可以发现：
当选定了一个元素，即 len(selects) == 1 的时候，接下来要选择 2 个元素， i 最大的值是 4 ，因为从 5 开始选择，就无解了。
当选定了两个元素，即 len(selects) == 2 的时候，接下来要选择 1 个元素， i 最大的值是 5 ，因为从 6 开始选择，就无解了。

3ddd55697423b5831cbbd42f4b901ebbade0daa456c651a70c758fe359d8a0d1-image - 副本.png

再如：如果 n = 6 ，k = 4，
len(selects) == 1 的时候，接下来要选择 3 个元素， i 最大的值是 4，最后一个被选的是 [4,5,6]；
len(selects) == 2 的时候，接下来要选择 2 个元素， i 最大的值是 5，最后一个被选的是 [5,6]；
len(selects) == 3 的时候，接下来要选择 1 个元素， i 最大的值是 6，最后一个被选的是 [6]；
再如：如果 n = 15 ，k = 4，
len(selects) == 1 的时候，接下来要选择 3 个元素，i 最大的值是 13，最后一个被选的是 [13,14,15]；
len(selects) == 2 的时候，接下来要选择 2 个元素， i 最大的值是 14，最后一个被选的是 [14,15]；
len(selects) == 3 的时候，接下来要选择 1 个元素， i 最大的值是 15，最后一个被选的是 [15]；
多写几遍（发现 max(i) 是我们倒着写出来），我么就可以发现 max(i) 与接下来要选择的元素貌似有一点关系，很容易知道：
max(i) + 接下来要选择的元素个数 - 1 = n，其中，接下来要选择的元素个数就是k - len(selects)，整理可得：

1	`max(i) = n - (k -len(selects)) + 1`

所以，我们的剪枝过程就是：把for循环的终止条件从 i < n+1 改成 i < n - (k - len(selects)) + 2

for i in range(first, n - (k - len(selects)) + 2):
    pre.append(i)
    backtrack(i + 1, selects)
    pre.pop()

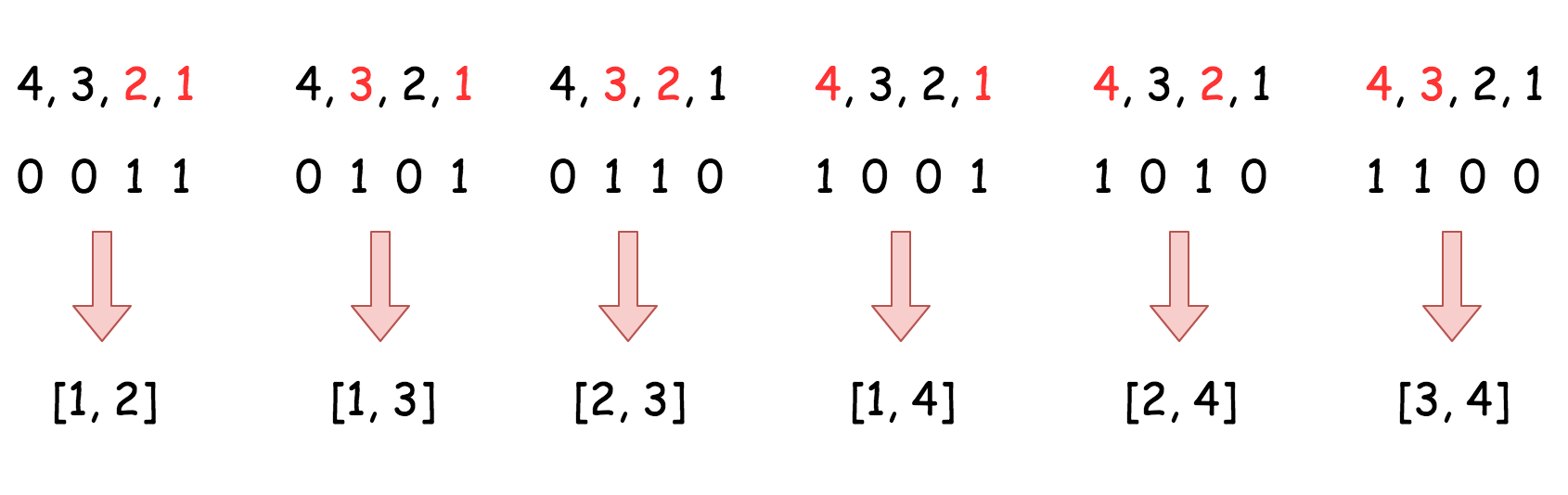
方法三、字典序 (二进制排序) 组合

主要思路是以字典序的顺序获得全部组合。

ab26203eb768a3153fe704cfee97158429d08e886f7e5b453b2256ee658f0598-image.png

算法
算法非常直截了当 :
- 将 nums 初始化为从 1 到 k的整数序列。将 n + 1添加为末尾元素，起到“哨兵”的作用。将指针设为列表的开头 j = 0. - While j < k : - 将nums 中的前k个元素添加到输出中，换而言之，除了“哨兵”之外的全部元素。 - 找到nums中的第一个满足 nums[j] + 1 != nums[j + 1]的元素，并将其加一 nums[j]++ 以转到下一个组合。

Python版本

方法一的实现

from typing import List

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        def backtrack(first=1, selects=[]):
            if len(selects) == k:
                res.append(selects[:])
                return
            for i in range(first, n+1):
                selects.append(i)
                backtrack(i+1, selects)
                selects.pop()
        # 特判
        if n <= 0 or k <= 0 or k > n:  return []
        if k == n:  return [list(range(1, n+1))]
        res = []
        backtrack()
        return res

Input = [2, 4, 1]
Input1 = [1, 2, 1]
Answer = [
    [[1],[2]],
    [
        [2,4],
        [3,4],
        [2,3],
        [1,2],
        [1,3],
        [1,4],
    ],
    [[1]]
]

if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)):
        print("-"*50)
        reslut = solution.combine(Input[i], Input1[i])
        if reslut == Answer[i]:
            print(True)
        else:
            print(False)
            print(reslut)
            print(Answer[i])

时间复杂度 : \(O(k C_N^k)\)，其中 \(C_N^k = \frac{N!}{(N - k)! k!}\) 是要构成的组合数。append / pop (add / removeLast) 操作使用常数时间，唯一耗费时间的是将长度为 k 的组合添加到输出中。
空间复杂度 : \(O(C_N^k)\) ，用于保存全部组合数以输出。
这里有两组运行结果：
1、执行用时 :604 ms, 在所有 Python3 提交中击败了37.44%的用户
内存消耗 :15.1 MB, 在所有 Python3 提交中击败了5.06%的用户
这一组代码在 res.append(selects[:]) 之后，没有 return。 2、执行用时 :508 ms, 在所有 Python3 提交中击败了66.70%的用户
内存消耗 :14.8 MB, 在所有 Python3 提交中击败了7.09%的用户
这一组代码在 res.append(selects[:]) 之后， return了，就没有执行后面的无效循环了，效率高了一些。

方法二的实现：剪枝版本的回溯算法

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        def backtrack(first=1, selects=[]):
            if len(selects) == k:
                res.append(selects[:])
                return
            # for i in range(first, n + 1):  # 剪枝之前 66.70%
            for i in range(first, n - (k - len(selects)) + 2):  # 剪枝之后 97.27%
                selects.append(i)
                backtrack(i+1, selects)
                selects.pop()
        # 特判
        if n <= 0 or k <= 0 or k > n:  return []
        if k == n:  return [list(range(1, n+1))]
        res = []
        backtrack()
        return res

时间复杂度 : \(O(k C_N^k)\)。
空间复杂度 : \(O(C_N^k)\) ，用于保存全部组合数以输出。
执行用时 :52 ms, 在所有 Python3 提交中击败了97.27%的用户
内存消耗 :15 MB, 在所有 Python3 提交中击败了5.31%的用户

方法三的实现：字典序 (二进制排序) 组合

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        # 特判
        if n <= 0 or k <= 0 or k > n:  return []
        if k == n:  return [list(range(1, n+1))]
         
        # init first combination
        nums = list(range(1, k + 1)) + [n + 1]
        
        output, j = [], 0
        while j < k:
            # add current combination
            output.append(nums[:k])
            # increase first nums[j] by one
            # if nums[j] + 1 != nums[j + 1]
            j = 0
            while j < k and nums[j + 1] == nums[j] + 1:
                nums[j] = j + 1
                j += 1
            nums[j] += 1
            
        return output

时间复杂度 : \(O(k C_N^k)\)，其中 \(C_N^k = \frac{N!}{(N - k)! k!}\) 是要构建的组合数。由于组合数是 \(C_N^k\) ，外层的 while 循环执行了 \(C_N^k\) 次。对给定的一个j，内层的 while 循环执行了 \(C_{N - j}^{k - j}\)。外层循环超过 \(C_N^k\)次访问，平均而言每次访问的执行次数少于1。因此，最耗费时间的部分是将每个长度为 \(k\)的组合(共计 \(C_N^k\) 个组合) 添加到输出中，消耗 \(O(k C_N^k)\) 的时间。你可能注意到，尽管方法三的时间复杂度与方法一相同，但方法三却要快上许多。这是由于基于回溯算法的方法一需要处理递归调用栈，且其带来的影响在Python中比在Java中更为显著。
空间复杂度 : \(O(C_N^k)\) ，用于保存全部组合数以输出。
这里有两组运行结果：
第一组是没有特判的，第二组是加上特判的结果。 1、执行用时 :68 ms, 在所有 Python3 提交中击败了93.57% 的用户
内存消耗 :14.9 MB, 在所有 Python3 提交中击败了6.58%的用户
2、执行用时 :40 ms, 在所有 Python3 提交中击败了 99.17%的用户
内存消耗 :14.9 MB, 在所有 Python3 提交中击败了5.82%的用户

剪枝和特判都会有效的提升算法运行效率。

参考链接

回溯算法 + 剪枝
 LeetCode题解

LeetCode

回溯算法

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

LeetCode 76. 最小覆盖子串（难）上一篇

LeetCode 75. 颜色分类（中）下一篇

LeetCode 77. 组合（中）

题目

示例

考察知识点

核心思想

Python版本