LeetCode 73. 矩阵置零（中）

纯数组题目，巧用第一行、第一列对结果进行存储。

6a4f63f58794b71cd4521a224fc1823ac5e4639e219dad519d0d8d8a421cf89f-image.png

题目

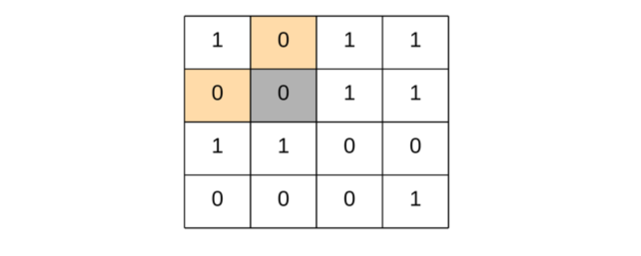
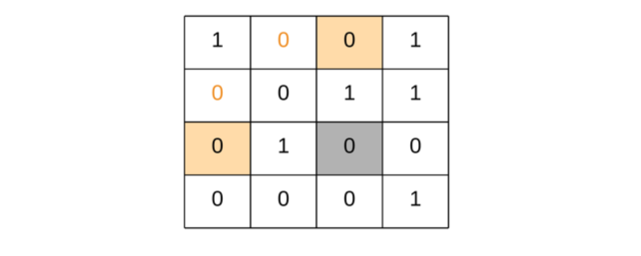
给定一个 m x n 的矩阵，如果一个元素为 0，则将其所在行和列的所有元素都设为 0。请使用原地算法。

示例

示例 1:

1
2
3
4
5
6
7
8
9
10
11
12
# 输入: 
[
  [1,1,1],
  [1,0,1],
  [1,1,1]
]
# 输出: 
[
  [1,0,1],
  [0,0,0],
  [1,0,1]
]

示例 2:

1
2
3
4
5
6
7
8
9
10
11
12
# 输入: 
[
  [0,1,2,0],
  [3,4,5,2],
  [1,3,1,5]
]
# 输出: 
[
  [0,0,0,0],
  [0,4,5,0],
  [0,3,1,0]
]

考察知识点

数组

核心思想

空间复杂度 \(O(n \times m)\) 的实现方法
直接新建一个和matrix等大小的矩阵，然后一行一行的扫，只要有0，就将新建的矩阵的对应行全赋0，行扫完再扫列，然后把更新完的矩阵赋给matrix即可。

空间复杂度 \(O(n + m)\) 的实现方法
用一个长度为m的一维数组记录各行中是否有0，用一个长度为n的一维数组记录各列中是否有0，最后直接更新matrix数组即可。

空间复杂度 \(O(1)\) 的实现方法 不能新建数组，我们考虑就用原数组的第一行第一列来记录各行各列是否有0。

  • 声明行和列为0的flag row_zero 和 col_zero， 先扫描第一行第一列，如果有0，则将各自的flag设置为true。
  • 然后扫描除去第一行第一列的整个数组，如果有0，则将对应的第一行和第一列的数字赋0，即当 matrix[i][j]==0 时，设置 matrix[0][j]=0 和 matrix[i][0]=0。
  • 再次遍历除去第一行第一列的整个数组，如果对应的第一行和第一列的数字有一个为0，即matrix[0][j]=0 或者 matrix[i][0]=0，则将当前值赋0。
  • 最后根据第一行第一列的flag来更新第一行第一列（注意这一个操作最后进行）。
6a4f63f58794b71cd4521a224fc1823ac5e4639e219dad519d0d8d8a421cf89f-image.png
a22aff099ed0c9aa58df2b30e375a72d7ae6bf00515ec16ebee1f181dbb3f4cb-image.png

Python版本

空间复杂度 \(O(1)\) 的实现方法，对第一行和第一列进行特殊处理，不用遍历整个 \(M \times N\) 的矩阵了，只用遍历\((M-1) \times (N-1)\) 的矩阵。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
from typing import List

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        if not len(matrix) or not len(matrix[0]): return
        m, n = len(matrix), len(matrix[0])
        rowZero, colZero = False, False
        # 判断第一行和第一列中是否有0
        for i in range(m):
            if matrix[i][0] == 0: colZero = True
        for i in range(n):
            if matrix[0][i] == 0: rowZero = True
        # 处理 m-1 * n-1 子矩阵
        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][j] == 0:
                    matrix[0][j] = 0
                    matrix[i][0] = 0
        # 更新 m-1 * n-1 子矩阵
        for i in range(1, m):
            for j in range(1, n):
                if matrix[0][j] == 0 or matrix[i][0] == 0:
                    matrix[i][j] = 0
        # 更新第一行、第一列
        if rowZero:
            for i in range(n): matrix[0][i] = 0
        if colZero:
            for i in range(m): matrix[i][0] = 0

Input = [
    [
        [1,1,1],
        [1,0,1],
        [1,1,1]
    ],
    [
        [0,1,2,0],
        [3,4,5,2],
        [1,3,1,5]
    ]
]
Answer = [
    [
        [1,0,1],
        [0,0,0],
        [1,0,1]
    ],
    [
        [0,0,0,0],
        [0,4,5,0],
        [0,3,1,0]
    ]
]

if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)):
        print("-"*50)
        solution.setZeroes(Input[i])
        if Input[i] == Answer[i]:
            print(True)
        else:
            print(False)
            print(Answer[i])
            print(Input[i])

时间复杂度：\(O(M-1 \times N-1)\)
空间复杂度：\(O(1)\)
执行用时 :44 ms, 在所有 Python3 提交中击败了95.11%的用户
内存消耗 :13.8 MB, 在所有 Python3 提交中击败了5.31%的用户

参考链接

LeetCode官方题解
Grandyang