LeetCode 72. 编辑距离（难）

经典的动态规划问题，有递归、非递归两种解法，注意状态转移方程的求解的逻辑。
dp[i-1][j] -> dp[i][j]是删除操作
dp[i][j-1] -> dp[i][j]是插入操作
dp[i][j] -> dp[i][j]是修改操作

题目

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作：

  1. 插入一个字符
  2. 删除一个字符
  3. 替换一个字符

示例

示例 1:

1
2
输入: word1 = "horse", word2 = "ros"
输出: 3
解释: 
1
2
3
1.horse -> rorse (将 'h' 替换为 'r')  
2.rorse -> rose (删除 'r')  
3.rose -> ros (删除 'e')
示例 2:
1
2
输入: word1 = "intention", word2 = "execution"
输出: 5
解释:
1
2
3
4
5
1.intention -> inention (删除 't')  
2.inention -> enention (将 'i' 替换为 'e')  
3.enention -> exention (将 'n' 替换为 'x')  
4.exention -> exection (将 'n' 替换为 'c')  
5. exection -> execution (插入 'u')

考察知识点

字符串、动态规划

核心思想

用动态规划 Dynamic Programming 来解。维护一个二维的数组 dp，其大小为 \(m \times n\)，\(m\) 和 \(n\) 分别为 word1 和 word2 的长度。dp[i][j] 表示从 word1 的前 i 个字符转换到 word2 的前 j 个字符所需要的最少步骤（或者说是word1 的前 i 个字母和 word2 的前 j 个字母之间的最小编辑距离）。
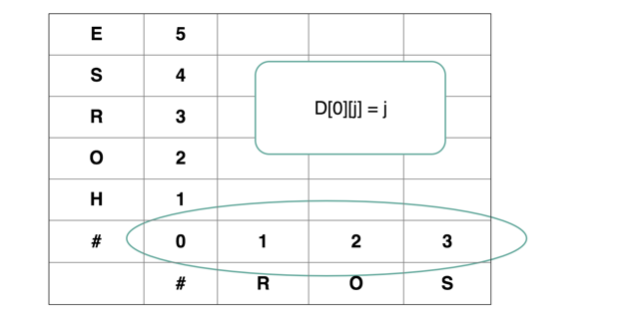
先给这个二维数组 dp 的第一行和第一列赋值，这个很简单，因为第一行和第一列对应的总有一个字符串是空串，一个空串和一个非空串的编辑距离为 d[i][0] = i 和 d[0][j] = j 于是转换步骤完全是另一个字符串的长度，下图的 # 代表空串。
第一行是 word1 为空变成 word2 最少步数，就是插入操作。换而言之，每一行从左往右就是在 insert，因此 dp[i][j-1] -> dp[i][j] 执行的是插入操作。
第一列，是 word2 为空，word1 变成 word2 需要的最少步数，就是删除操作。换而言之，每一列从下往上就是在 delete ，因此 dp[i-1][j] -> dp[i][j] 执行的是删除操作。

dp.png

初始化了dp 的第一行和第一列之后，就要确定状态转移方程，由前述可知。
- dp[i-1][j] -> dp[i][j]是删除操作
- dp[i][j-1] -> dp[i][j]是插入操作
- dp[i][j] -> dp[i][j]是修改操作

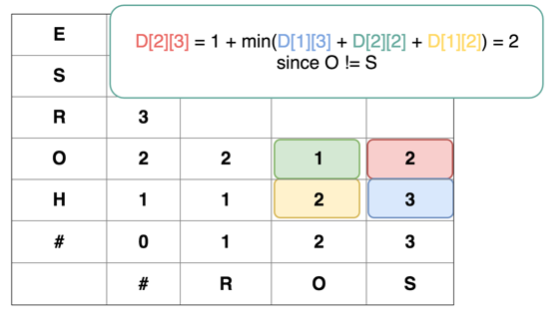
所以，通过观察可以发现， 当第i 个字符 和 第 j 个字符不等时， 状态转移方程是 \(dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])\) 。

1

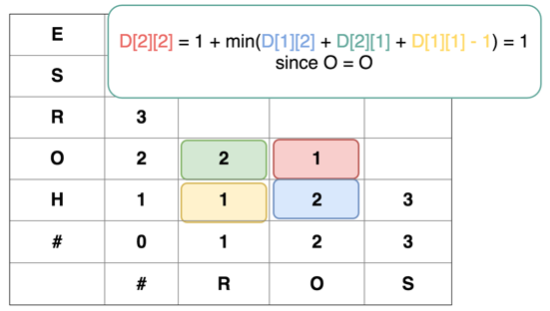
当第i 个字符 和 第 j 个字符相等时，不需要做任何操作， 所以状态转移方程是 \(dp[i][j] = dp[i-1][j-1]\) 该状态转移方程等效于 \(dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]-1)\) 。

dp1.png

在动态规划之前，可以做个优化，循环判断 word1 和 word2 最后一位字母是否相同，可以通过 word1 = word1[:-1] 和 word2 = word2[:-1] 去除掉最后一位，因为最后一位如果相同，就不用编辑最后一位了，去掉也不影响 res 计算，还能减少 dp 占用内存的大小。

1
2
3
4
5
res = 0
while word1[-1] == word2[-1]:
	word1 = word1[:-1]
	word2 = word2[:-1]
# 开展后续计算res的操作

清楚了状态转移方程之后，就可以写代码了。该动态规划算法的实现，可以以循环形式实现，也可以递归形式实现。

Python版本

  • 循环形式的动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from typing import List

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        # 进行预处理 缩小额外空间大小
        while len(word1) and len(word2) and word1[-1] == word2[-1]:
            word1 = word1[:-1]
            word2 = word2[:-1]
        # 进行特判
        if word1 == "": return len(word2)
        if word2 == "": return len(word1)
        # 声明dp矩阵
        m = len(word1)
        n = len(word2)
        dp = [[0 for _ in range(n+1)] for _ in range(m+1)]
        # 初始化dp矩阵的
        for i in range(m+1): dp[i][0] = i
        for j in range(n+1): dp[0][j] = j
        # 开始循环进行动态规划
        for i in range(1, m+1):
            for j in range(1, n+1):
                if word1[i-1] == word2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])

        return dp[-1][-1]

Input = ["a", "horse", "inten", "intention"]
Input1 = ["a", "ros", "execu", "execution"]
Answer = [0, 3, 5, 5]

if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)):
        print("-"*50)
        reslut = solution.minDistance(Input[i], Input1[i])
        if reslut == Answer[i]:
            print(True)
        else:
            print(False)
            print(Answer[i])
            print(reslut)

时间复杂度：\(O(m' \times n')\)，\(m'\) 和 \(n'\) 分别是去掉尾部同样字符之后的 word1 和 word2 的长度。
空间复杂度：\(O(m' \times n')\)，关于\(m'\) 和 \(n'\)，同上。
执行用时 :192 ms, 在所有 Python3 提交中击败了68.49%的用户
内存消耗 :17.1 MB, 在所有 Python3 提交中击败了12.41%的用户

  • 递归形式的动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        def dp(word1, i, word2, j, memo):
            if i == len(word1): return int(len(word2) - j)  # 判断是否达到边界
            if j == len(word2): return int(len(word1) - i)  # 判断是否达到边界
            if memo[i][j] > 0: return memo[i][j]  # if memo中保存了该状态 return mono中该状态的保存结果
            res = 0
            if word1[i] == word2[j]:
                return dp(word1, i+1, word2, j+1, memo)
            else:
                insertCnt = dp(word1, i, word2, j+1, memo)
                deletaCnt = dp(word1, i+1, word2, j, memo)
                replaceCnt = dp(word1, i+1, word2, j+1, memo)
                res = min(insertCnt, deletaCnt, replaceCnt) + 1
            memo[i][j] = res
            return res

        m, n = len(word1), len(word2)
        memo = [[0 for _ in range(n+1)] for _ in range(m+1)] # 声明dp矩阵 保存计算结果
        return dp(word1, 0, word2, 0, memo)  # 开始递归进行动态规划

执行用时 :328 ms, 在所有 Python3 提交中击败了11.84%的用户
内存消耗 :16.7 MB, 在所有 Python3 提交中击败了13.40%的用户

参考连接

Grandyang
花花酱
喜刷刷