LeetCode 69. x 的平方根（易）

一个简单难度的题目，要理解使用拟牛顿法解决问题的原理。

题目

实现 int sqrt(int x) 函数。
计算并返回 x 的平方根，其中 x 是非负整数。
由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例

示例 1:

1
2
输入: 4
输出: 2

示例 2:

1
2
输入: 8
输出: 2

说明: 8 的平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

考察知识点

二分查找、数学

核心思想

方法一、二分查找
算一个候选值的平方，然后和 \(x\) 比较大小，为了缩短查找时间，我们采用二分搜索法来找平方根，找最后一个不大于目标值的数。 之前 left 和 right 都是数组下标，这里的 left 和 right 直接就是数字本身了，一个数字的平方根是不可能比起本身还大的，所以 right 初始化为 \(x\)，还有就是这里若 \(x\) 是整型最大值，再加1就会溢出。最后就是返回值是 right-1，因为题目中说了要把小数部分减去，只有减1才能得到正确的值。

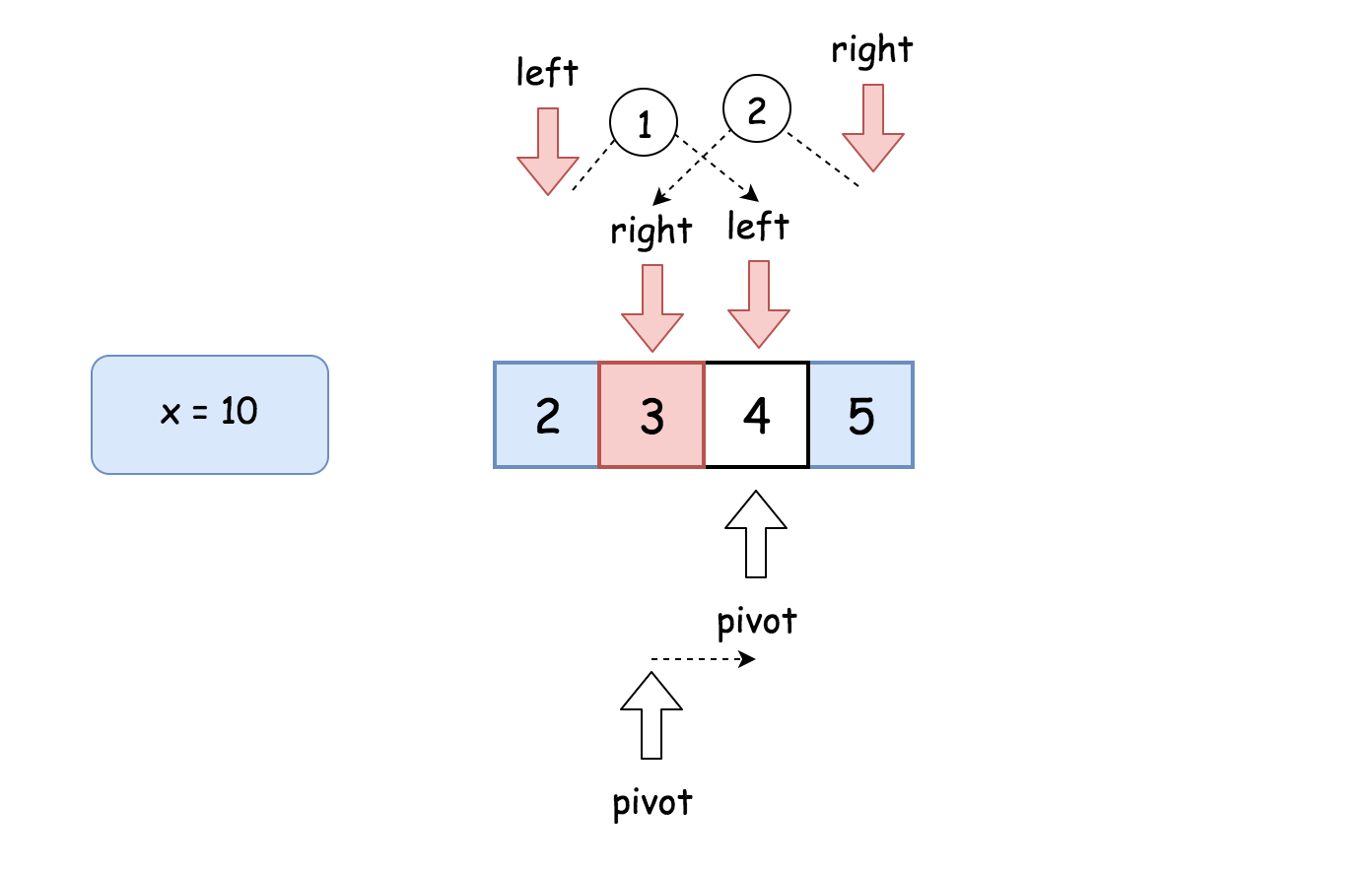
另外一种二分法解法的实现，从x/2处开始寻找。

  • 如果 x < 2，返回 x。
  • 令左边界为 2，右边界为 x / 2。
  • 当 left <= right 时：
    • 令 num = (left + right) / 2，比较 num * num 与 x：
      • 如果 num * num > x，更新右边界为 right = pivot -1。
      • 如果 num * num < x，更新左边界为 left = pivot + 1。
      • 如果 num * num == x，即整数平方根为 num，返回 num。
  • 返回 right。
binary

方法二、牛顿迭代法
利用牛顿迭代法，高数中好像讲到过这个方法，是用逼近法求方程根的神器，在这里也可以借用一下，可参见网友 Annie Kim's Blog 的博客。 为了方便理解，就先以本题为例：
计算 \(x^2 = n\) 的解，令 \(f(x)=x^2-n\) ，相当于求解 \(f(x)=0\) 的解，如下图所示。
首先取 \(x_0\)，如果 \(x_0\) 不是解，做一个经过 \((x_0, f(x_0))\) 这个点的切线，与x轴的交点为 \(x_1\)。
同样的道理，如果 \(x_1\) 不是解，做一个经过 \((x_1,f(x_1))\) 这个点的切线，与x轴的交点为 \(x_2\) 。
以此类推。

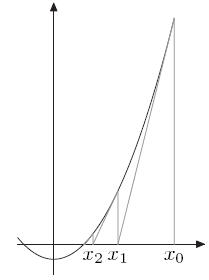
18155235-b272cc444a1845d3aede4c72a87f83dc.jpg

以这样的方式得到的 \(x_i\)会无限趋近于 \(f(x)=0\) 的解。
判断 \(x_i\) 是否是 \(f(x)=0\) 的解有两种方法：
一是直接计算 \(f(x_i)\) 的值判断是否为 \(0\)，二是判断前后两个解 \(x_i\) 和 \(x_{i-1}\) 是否无限接近。
经过 \((x_i, f(x_i))\) 这个点的切线方程为 \(f(x) = f(x_i) + f’(x_i)(x - x_i)\) ，其中 \(f'(x)\) 为 \(f(x)\) 的导数，本题中为\(2x\)。令切线方程等于0，即求解出的 \(x\) 就是 \(x_{i+1}\)， \(x_{i+1}=x_i - f(x_i)/f’(x_i)\)。 继续化简，\(x_{i+1}=x_i - (x_i^2 - n) / (2x_i) = x_i - x_i / 2 + n / (2x_i) = x_i / 2 + n / 2x_i = (xi + n/xi) / 2\)。
即，\(x_{i+1}=(xi + n/xi) / 2\) 有了迭代公式，程序就好写了，关于牛顿迭代法，可以参考wikipedia以及百度百科。

算法效率比较

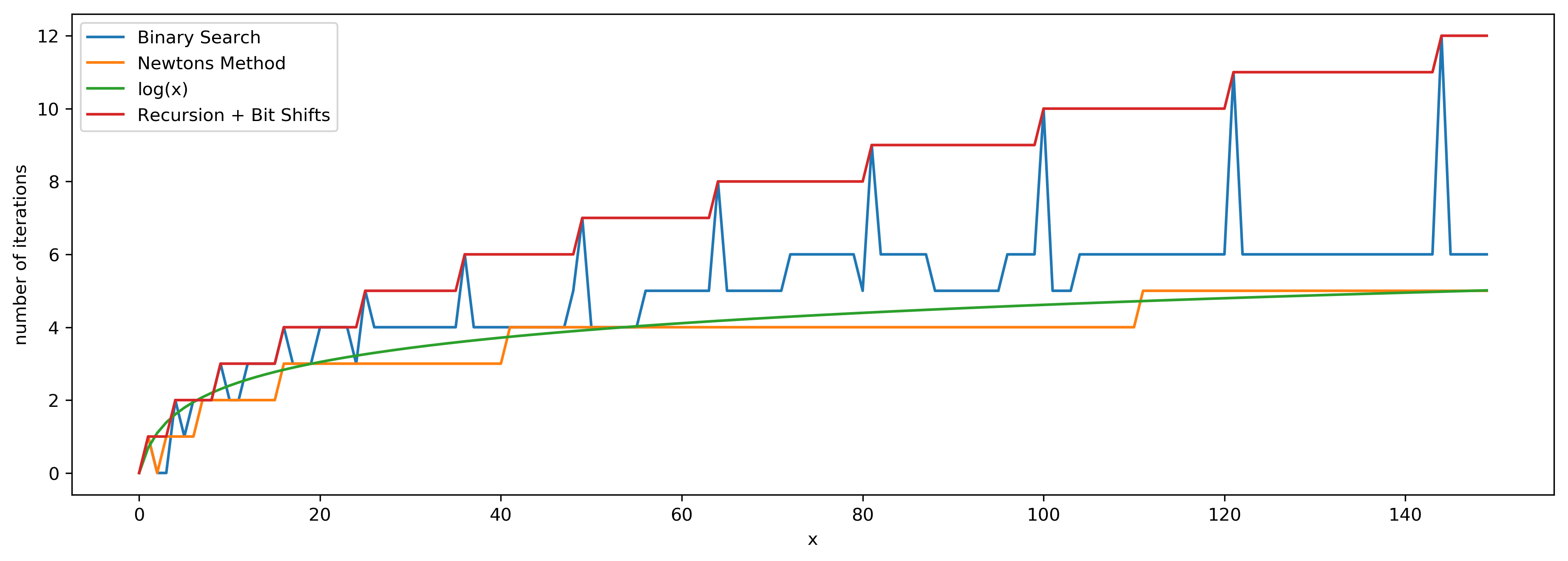
cp.png

牛顿法随着x的增加性能优势也在增加

Python版本

  • 方法一的实现
1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def mySqrt(self, x: int) -> int:
        if x <= 1: return x
        left, right = 0, x
        while left < right:
            mid = left + (right - left) // 2
            if mid * mid <= x:  # 如果 mid*mid是不大于x的，即平方根在右区间，右移left。
                left = mid + 1
            else:  # 否则，如果mid*mid大于x，说明平方根在左区间，左移right。
                right = mid
        return right - 1

时间复杂度：\(O(logN)\)。
空间复杂度：\(O(1)\)。
执行用时 :40 ms, 在所有 Python3 提交中击败了74.38%的用户
内存消耗 :13.3 MB, 在所有 Python3 提交中击败了5.02%的用户

另外一种二分法解法的实现，从x/2处开始寻找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def mySqrt(self, x):
        if x < 2:
            return x
        
        left, right = 2, x // 2
        
        while left <= right:
            pivot = left + (right - left) // 2
            num = pivot * pivot
            if num > x:
                right = pivot -1
            elif num < x:
                left = pivot + 1
            else:
                return pivot
            
        return right

执行用时 :68 ms, 在所有 Python3 提交中击败了18.20%的用户
内存消耗 :13.5 MB, 在所有 Python3 提交中击败了5.02%的用户

  • 方法二的实现
1
2
3
4
5
6
class Solution:
    def mySqrt(self, x: int) -> int:
        res = x
        while (res * res) > x:
            res = (res + x // res) // 2
        return int(res)

时间复杂度：\(O(logN)\)，此方法是二次收敛的。
空间复杂度：\(O(1)\)。
执行用时 :68 ms, 在所有 Python3 提交中击败了18.20%的用户
内存消耗 :13.5 MB, 在所有 Python3 提交中击败了5.02%的用户

  • python内建求平方根的方法
1
2
3
class Solution:
    def mySqrt(self, x: int) -> int:
        return int(x ** 0.5)

执行用时 :52 ms, 在所有 Python3 提交中击败了38.08%的用户 内存消耗 :13.2 MB, 在所有 Python3 提交中击败了5.02%的用户

参考链接

Grandyang
LeetCode 官方题解

相似题目

367. 有效的完全平方数（易） （已完成）