LeetCode 62. 不同路径（中）

一道经典的基于递归的动态规划问题

Snipaste_2020-03-17_13-28-22.png

题目

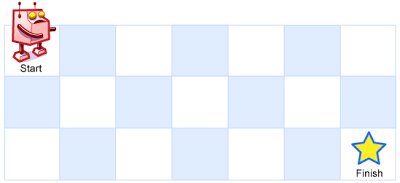
一个机器人位于一个 m(列数) x n(行数) 网格的左上角 （起始点在下图中标记为“Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
问总共有多少条不同的路径？

Snipaste_2020-03-17_13-28-22.png

例如，上图是一个7 x 3 的网格。有多少可能的路径？

提示：
1 <= m, n <= 100
题目数据保证答案小于等于 \(2 * 10 ^ 9\)

示例

示例 1:

1
2
输入: m = 3, n = 2
输出: 3

解释:
从左上角开始，总共有 3 条路径可以到达右下角。

  1. 向右 -> 向右 -> 向下
  2. 向右 -> 向下 -> 向右
  3. 向下 -> 向右 -> 向右

示例 2:

1
2
输入: m = 7, n = 3
输出: 28

考察知识点

数组、动态规划

核心思想

方法一、排列组合

因为机器到底右下角，向下几步，向右几步都是固定的，
比如，m=3, n=2，我们只要向下 1 步，向右 2 步就一定能到达终点。
所以有 \(C_{m+n-2}^{m-1}\)，使用排列组合策略，实际上就是在用回溯算法。

方法二、动态规划

我们令 dp[i][j] 是到达 i , j 最多路径
动态方程：dp[i][j] = dp[i-1][j] + dp[i][j-1]
注意，对于第一行 dp[0][j]，或者第一列 dp[i][0]，由于都是在边界，所以只能为 1。
时间复杂度：\(O(m*n)\)
空间复杂度：\(O(m * n)\)
优化：因为我们每次只需要 dp[i-1][j],dp[i][j-1]所以我们只要记录这两个数。

解释
dp矩阵中每个位置上的数值代表到达这个位置的路径的个数
因为只能往下和往右走的，所以当前位置 dp[i][j] 的到达路径个数，只能由上面位置 dp[i-1][j] 和左边位置 dp[i][j-1] 上的值之和决定，所以动态方程是 dp[i][j] = dp[i-1][j] + dp[i][j-1]。
最简单易懂的情况，空间复杂度为\(O(n^2)\)

Python版本

  • 方法一实现
1
2
3
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        return int(math.factorial(m+n-2)/math.factorial(m-1)/math.factorial(n-1))

执行用时 :24 ms, 在所有 Python3 提交中击败了98.27%的用户
内存消耗 :13.5 MB, 在所有 Python3 提交中击败了5.38%的用户

  • 方法二实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
# 写法一、最简单易懂的情况，空间复杂度为O(n^2)
# 每个位置上的数值代表到达这个位置的路径的个数
# 因为是往下和往右走的，所以当前位置的到达路径个数，由上面和左边位置上的值之和决定。
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [[1]*m] + [[1]+[0] * (m-1) for _ in range(n-1)]
        for i in range(1, n):
            for j in range(1, m):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
        return dp[-1][-1]

# 写法二
# 优化空间复杂度为O(2n)
# n行 * m列
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        pre = [1] * m  # 一行一行的计算 pre为上一行m个位置每个位置达到当前位置的路径的个数
        cur = [1] * m  # cur为当前行m个位置每个位置达到当前位置的路径的个数
        for _ in range(1, n):  # 第一行必然是只有一条路径能达到该位置，所以不必计算了，range函数从1开始。
            for j in range(1, m):  # 同理，第一列必然只有一条路径达到该位置，所以不必计算，range函数也从1开始。
                cur[j] = pre[j] + cur[j-1]  # 当前位置等于上一行这一列pre[j]加上这一行前一列cur[j-1]
            pre = cur[:]  # 由于list是可变对象，所以采用[:]将cur的值赋给pre，然后再计算下一行
        return pre[-1]


# 写法三、优化空间复杂度为 O(n)
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        cur = [1] * m  # 这里只用一行就行
        for _ in range(1, n):
            for j in range(1, m):
                cur[j] += cur[j-1]  # 等效于 cur[j] = cur[j] + cur[j-1]，其中cur[j]是当前位置上方位置的数值，也就是dp[i-1][j]。cur[j-1]是当前位置左边位置的数值，也就是dp[i][j-1]
        return cur[-1]

print("leet code accept!!!")
Input = [3, 7]
Input1 = [2, 3]
Answer = [3, 28]


if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)):
        print("-"*50)
        reslut = solution.uniquePaths(Input[i], Input1[i])
        print(reslut == Answer[i])

空间复杂度：\(O(n^2)\)
执行用时 :28 ms, 在所有 Python3 提交中击败了93.53%的用户。
内存消耗 :13.5 MB, 在所有 Python3 提交中击败了5.38%的用户。

有效语法糖

1
2
 # 一种声明矩阵方法，保证第一行和第一列全是1
dp = [[1]*m] + [[1]+[0] * (m-1) for _ in range(n-1)]

参考连接

力扣（LeetCode）powcai