LeetCode 53. 最大子序和（易）& 剑指offer 面试题42. 连续子数组的最大和（易）

动态规划、分治算法的应用

题目

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。 如果你已经实现复杂度为 \(O(n)\) 的解法，尝试使用更为精妙的分治法求解。

测试用例

功能测试（输入的数组中有正数也有负数；输入的数组中全是正数；输入的数组中全是负数）。 特殊输入测试（表示数组的指针为nullptr指针）。

本题考点

考查应聘者对时间复杂度的理解。这道题如果应聘者给出时间复杂度为 \(O(n^2)\) 甚至 \(O(n^3)\) 的算法，则是不能通过面试的。考查应聘者对动态规划的理解。如果应聘者熟练掌握了动态规划算法，那么他就能轻松地找到解题方案。如果没有想到用动态规划的思想，那么应聘者就需要仔细地分析累加子数组的和的过程，从而找到解题的规律。 考查应聘者思维的全面性。能否合理地处理无效的输入，对面试结果有很重要的影响。

示例

1
2
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6

解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

考察知识点

数组、分治算法、动态规划

核心思想

分治算法

下面是用分治法解决问题的模板： 1、定义基本情况。 2、将问题分解为子问题并递归地解决它们。 3、合并子问题的解以获得原始问题的解。

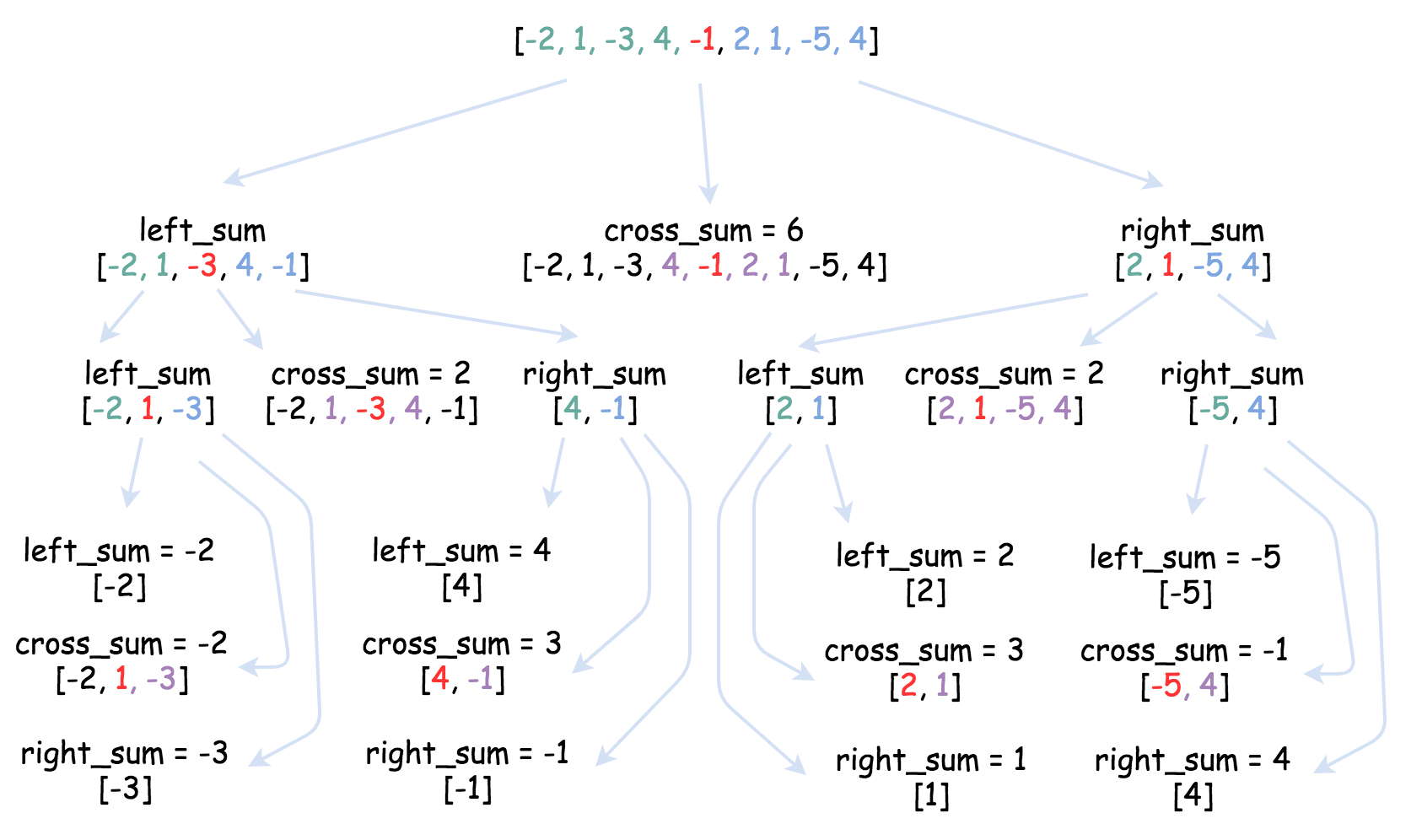
将数组二分为两部分nums1[]、nums2[]，则最大子序和一定是下面三种情况中的一种： 1、最大子序和在nums1[]中 2、最大子序和在nums2[]中 3、最大子序和跨越nums1和nums2，此时需计算nums1[]中从右端点开始（包含右端点）的最大子序的数值和以及nums2[]中从左端点开始（包含左端点）的最大自序的数值和，求这两个最大自序和之和。

1.png

动态规划（Kadane 算法）

在整个数组或在固定大小的滑动窗口中找到总和或最大值或最小值的问题可以通过动态规划（DP）在线性时间内解决。 有两种标准 DP 方法适用于数组：
1. 常数空间，沿数组移动并在原数组修改。
2. 线性空间，首先沿 left->right 方向移动，然后再沿 right->left 方向移动。 合并结果。

我们在这里使用第一种方法，因为可以修改数组跟踪当前位置的最大和。下一步是在知道当前位置的最大和后更新全局最大和。

算法

  • 得到 nums 长度。
  • 设置第一值为默认最大和 max_sum 。
  • 依次遍历。
    • 如果前一个 cur_sum 是正数，当前值 nums[i] 加上前一个 cur_sum（由于 cur_sum 就保存在 nums 中，所以是加上 nums[i-1]）。这里是把累加和 cur_sum 保存在原来的数组 nums 里面了。
    • 如果前一个 cur_sum 是负数，选择当前值 nums[i] 和最大和 max_sum 两者中最大的那个值为新的最大和。
  • 返回最大和 max_sum 。
picture

一张表格说清楚

以 [1, -2, 3, 10, -4, 7, 2, -5] 为例，当加3时，前一个 cur_sum 为负数，即就选择 max_sum(1) 和 nums[i](3) 中较大的那一个，也就是3，作为新的 max_sum。当全部遍历之后，返回最终的 max_sum(18) 即可。

num 1 -2 3 10 -4 7 2 -5
cur_sum(dp) 1 -1 3 13 9 16 18 13
max_sum 1 1 3 13 13 16 18 18

贪心算法

使用单个数组作为输入来查找最大（或最小）元素（或总和）的问题，贪心算法是可以在线性时间解决的方法之一。每一步都选择最佳方案，到最后就是全局最优的方案。

算法： 该算法通用且简单：遍历数组并在每个步骤中更新：当前元素 current element、当前元素位置的最大和 current max sum 、迄今为止的最大和 mas sum seen so far

  • 得到 nums长度，设置当前元素位置的最大和 max_sum、迄今为止的最大 curr_sum。
  • 开始遍历，1-(n-1)。
    • 从当前值 nums[i] 及其当前元素位置的最大和之和 curr_sum + nums[i] 之间选择一个最大值作为当前元素位置的最大和 curr_sum 。
    • 从当前元素位置的最大和 curr_sum、当前迄今为止的最大 curr_sum 中，选择一个作为新的迄今为止的最大 curr_sum 。
  • 最终返回迄今为止的最大 curr_sum 。
2.png

上图蓝色箭头表示当前字符串起点位置，一直保持在使得和最大的位置，直到遍历到最后一个元素。单步最优解为 max_sum = max(max_sum, max(nums[i], curr_sum + nums[i])) 。

LeetCode题解

Python版本

分治算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution:
    def cross_sum(self, nums, left, right, p): 
            if left == right:
                return nums[left]

            left_subsum = float('-inf')
            curr_sum = 0
            for i in range(p, left - 1, -1):
                curr_sum += nums[i]
                left_subsum = max(left_subsum, curr_sum)

            right_subsum = float('-inf')
            curr_sum = 0
            for i in range(p + 1, right + 1):
                curr_sum += nums[i]
                right_subsum = max(right_subsum, curr_sum)

            return left_subsum + right_subsum   
    
    def helper(self, nums, left, right): 
        if left == right:
            return nums[left]
        
        p = (left + right) // 2
            
        left_sum = self.helper(nums, left, p)
        right_sum = self.helper(nums, p + 1, right)
        cross_sum = self.cross_sum(nums, left, right, p)
        
        return max(left_sum, right_sum, cross_sum)
        
    def maxSubArray(self, nums: 'List[int]') -> 'int':
        return self.helper(nums, 0, len(nums) - 1)

时间复杂度：\(O(N \log N)\)。
空间复杂度：\(O(\log N)\)，递归时栈使用的空间。
执行用时 :144 ms, 在所有 Python3 提交中击败了10.27%的用户
内存消耗 :14.2 MB, 在所有 Python3 提交中击败了22.59%的用户

动态规划（Kadane 算法）

1
2
3
4
5
6
7
8
9
10
class Solution:
    def maxSubArray(self, nums: 'List[int]') -> 'int':
        n = len(nums)  # 得到nums长度
        max_sum = nums[0]  # 设置第一值为默认最大和
        for i in range(1, n):  # 依次遍历
            if nums[i - 1] > 0:  # 当前一个是正数时当前值nums[i]加上前一个值nums[i-1]，否则跳过。这里等于说是把累加和保存在原来的数组nums里面了。
                nums[i] += nums[i - 1] 
            max_sum = max(nums[i], max_sum)  # 选择当前值nums[i]和最大和max_sum两者中最大的那个值为新的最大和

        return max_sum  # 返回最大和 max_sum

时间复杂度：\(O(N)\)。只遍历了一次数组。
空间复杂度：\(O(1)\)，使用了常数的空间。
执行用时 :52 ms, 在所有 Python3 提交中击败了90.50%的用户
内存消耗 :14.4 MB, 在所有 Python3 提交中击败了21.63%的用户

贪心算法

1
2
3
4
5
6
7
8
9
class Solution:
    def maxSubArray(self, nums: 'List[int]') -> 'int':
        n = len(nums)  # 得到nums长度
        curr_sum = max_sum = nums[0]  # 设置当前元素位置的最大和max_sum、迄今为止的最大curr_sum
        for i in range(1, n):  # 开始遍历
            curr_sum = max(nums[i], curr_sum + nums[i])  # 从当前值nums[i]及其当前元素位置的最大和之和curr_sum + nums[i] 之间选择一个最大值作为当前元素位置的最大和curr_sum
            max_sum = max(max_sum, curr_sum)  # 从当前元素位置的最大和curr_sum、当前迄今为止的最大curr_sum中，选择一个作为新的迄今为止的最大curr_sum
            
        return max_sum  # 最终返回迄今为止的最大curr_sum

时间复杂度：\(O(N)\)。只遍历一次数组。
空间复杂度：\(O(1)\)，只使用了常数空间。
执行用时 :48 ms, 在所有 Python3 提交中击败了93.17%的用户
内存消耗 :14 MB, 在所有 Python3 提交中击败了22.63%的用户