经典的回溯算法问题，约束编程加回溯法。

题目

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上（也就是每一行/列，都要有一个皇后），并且使皇后彼此之间不能相互攻击（即任意2个皇后不允许处在同一排，同一列，也不允许处在与棋盘边框成45角的斜线上）。

8-queens.png

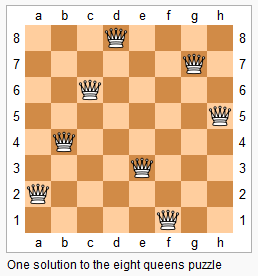
上图为 8 皇后问题的一种解法。
给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例

输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

考察知识点

回溯算法

核心思想

首先，介绍两个有用的编程概念。

第一个叫做 约束编程。

它的基本含义是在放置每个皇后以后增加限制。当在棋盘上放置了一个皇后后，立即排除当前行，列和对应的两个对角线。该过程传递了 约束 从而有助于减少需要考虑情况数。

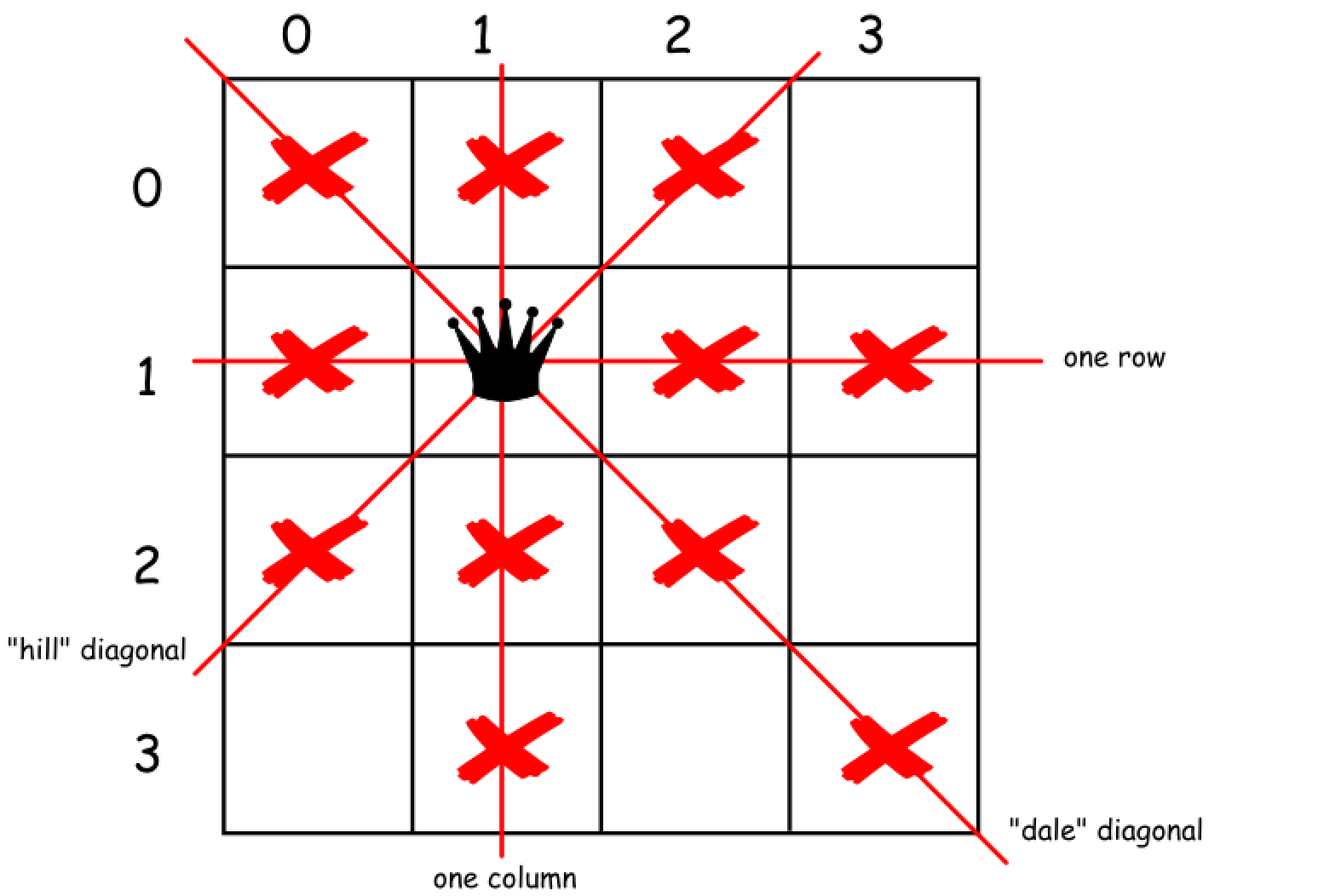
第二个叫做 回溯法。

我们来想象一下，当在棋盘上放置了几个皇后且不会相互攻击。但是选择的方案不是最优的，因为无法放置下一个皇后。此时我们该怎么做？回溯。意思是回退一步，来改变最后放置皇后的位置并且接着往下放置。如果还是不行，再回溯。

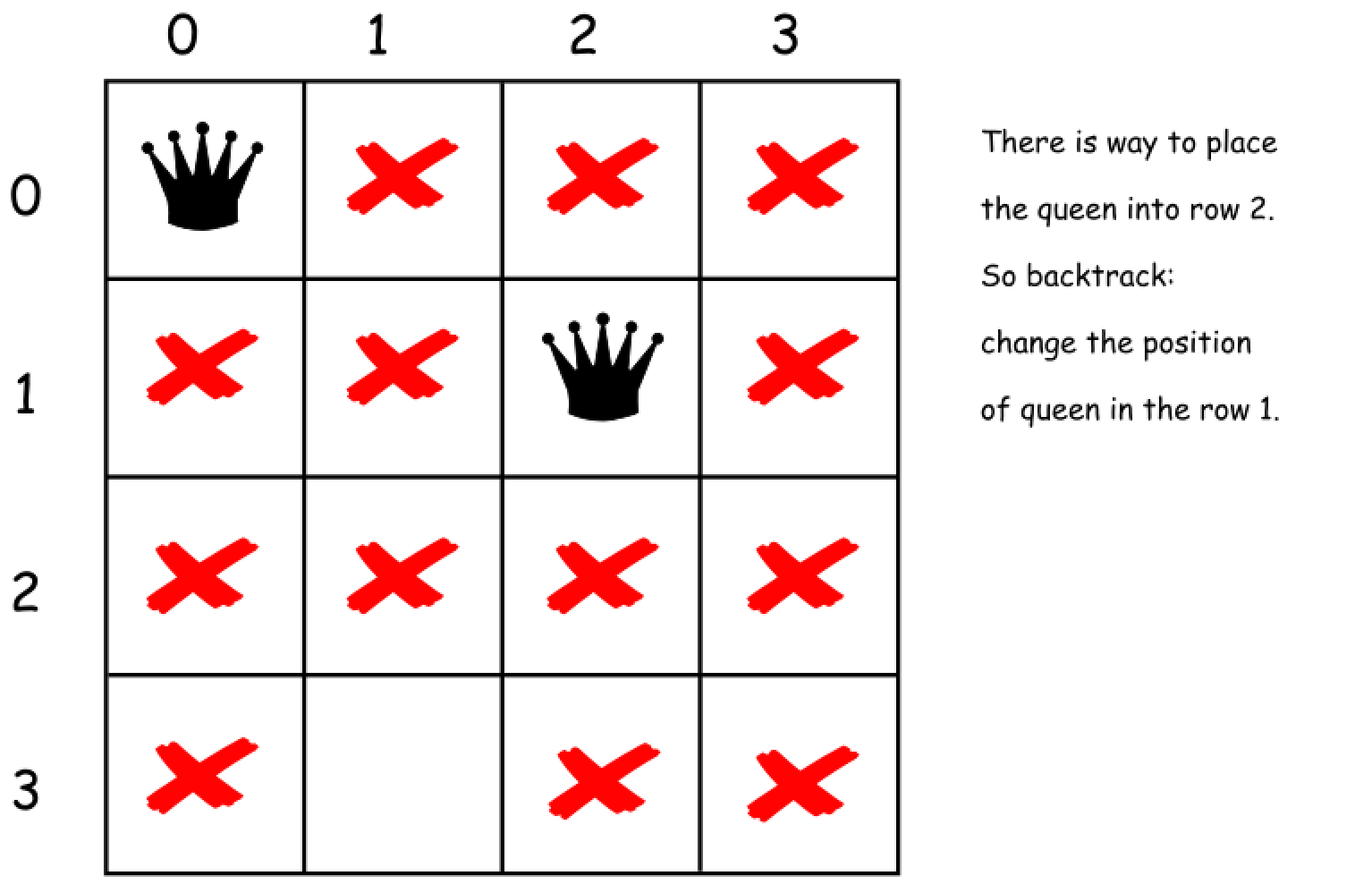
在建立算法之前，我们来考虑两个有用的细节。
- 一行只可能有一个皇后且一列也只可能有一个皇后。
这意味着没有必要再棋盘上考虑所有的方格。只需要按列循环即可。
- 对于所有的主对角线（左上到右下）有 行号 - 列号 = 常数，对于所有的次对角线（右上到左下）有 行号 + 列号 = 常数。

这可以让我们标记已经在攻击范围下的对角线并且检查一个方格 (行号, 列号) 是否处在攻击位置。
基于回溯法三要素，选择列表（Constraint）、路径（Choice）、结束条件（Goal），现在已经可以写回溯函数 backtrack(row = 0)。

• 从第一个 row = 0 开始.
• 循环列并且试图在每个 column 中放置皇后.
• 如果方格 (row, column) 不在攻击范围内，这是选择列表（Our Constraints）。
  • <选择> 在 (row, column) 方格上放置皇后。row, column是路径（Our Choice）。
    • 排除对应行，列和两个对角线的位置。
    • <结束条件（Our Goal）> If 所有的行被考虑过，即row == N 。
      • 意味着我们找到了一个解。
    • Else
      • <回溯> 继续考虑接下来的皇后放置 backtrack(row + 1)。
      • <撤销选择> 将在 (row, column) 方格的皇后移除。

LeetCode题解

Python版本

回溯方法实现

class Solution:
    def solveNQueens(self, n: int) -> list:
        def could_place(row, col):
            return not (cols[col] + hill_diagonals[row - col] + dale_diagonals[row + col])  # 判断该位置是否被排除，只有cols[col]、hill_diagonals[row - col]、dale_diagonals[row + col])都处于0（即没有被排除）的情况下才能认为是该位置可用
        
        def place_queen(row, col):
            queens.add((row, col))  # 添加确认的位置到queens
            cols[col] = 1  # 标记该列无法再添加
            hill_diagonals[row - col] = 1  # 希尔对角线 即 主对角线 行号-列号=常数，通过记录这个常数，之后只要判断行号-列号=该常数的位置，都无法再添加皇后了。
            dale_diagonals[row + col] = 1  # 戴尔对角线 即 次对角线 行号+列号=常数，通过记录这个常数，之后只要判断行号+列号=该常数的位置，都无法再添加皇后了。
        
        def remove_queen(row, col):
            queens.remove((row, col))  # 解除该位置的占用
            cols[col] = 0  # 同时解除该位置的列占用
            hill_diagonals[row - col] = 0  # 同时解除该位置的主对角线占用
            dale_diagonals[row + col] = 0  # 同时解除该位置的次对角线的占用
        
        def add_solution():
            solution = []
            for _, col in sorted(queens):  # 开始将位置转化成.Q..的形式 使用_为占位符，VS Code不会报错。
                solution.append('.' * col + 'Q' + '.' * (n - col - 1))
            output.append(solution)

        def backtrack(row = 0):  # 默认backtrack从第0行开始
            for col in range(n):  # 逐列添加
                if could_place(row, col):  # 判断当前位置是否可以添加皇后
                    place_queen(row, col)  # 可以添加，就将皇后添加上去。
                    if row + 1 == n:  # 结束条件 Our Goal 遍历完所有行
                        add_solution()  # 全部n行都遍历完了就添加一个找到的结果
                    else:
                        backtrack(row + 1)  # 否则去回溯当前行的下一行 row+1， 列不变
                    remove_queen(row, col)  # 如果发现不行，回就回溯回来，把刚刚放置了皇后的节点给删除了。
        
        cols = [0] * n
        hill_diagonals = [0] * (2 * n - 1)  # 如果输入棋盘是固定的，那么hill_diagonals和dale_diagonals可能出现的情况个数也是固定的，就是2 * n - 1
        dale_diagonals = [0] * (2 * n - 1)
        queens = set()  # 这里使用的是set，注意set的添加用add，删除直接用remove就行。
        output = []
        backtrack()
        return output

print("leet code accept!!!")
Input = [4]
Input1 = [2]
Answer = [
    [
        [".Q..",  # 解法 1
        "...Q",
        "Q...",
        "..Q."],

        ["..Q.",  # 解法 2
        "Q...",
        "...Q",
        ".Q.."]
    ]
]

if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)):
        print("-"*50)
        result = solution.solveNQueens(Input[i])
        print(result)
        print(Answer[i])

时间复杂度：\(O(N!)\)， 放置第 1 个皇后有 N 种可能的方法，放置两个皇后的方法不超过 N (N - 2) ，放置 3 个皇后的方法不超过 N(N - 2)(N - 4) ，以此类推。总体上，时间复杂度为 \(\mathcal{O}(N!)\)。 空间复杂度：\(O(N)\). 需要保存对角线和行的信息。

有效语法糖

1、使用_为占位符，不会出现Python3 Warming。

for _,value in range(n):
	print(value)