将给定的矩阵分成四个矩形 并且将原问题划归为旋转这些矩形的问题。

题目

给定一个 n × n 的二维矩阵表示一个图像。 将图像顺时针旋转 90 度。

说明： 你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例

示例 1:

给定 matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],
原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

示例 2:

给定 matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 
原地旋转输入矩阵，使其变为:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

考察知识点

数组

核心思想

方法一、转置加翻转

最直接的想法是先转置矩阵，然后翻转每一行。这个简单的方法已经能达到最优的时间复杂度\(O(N^2)\)。

算法

• 根据输入数据，得到 n 的大小。
• 先获得转置矩阵
• 列号从0 一直到 n-1，外循环是列 i 代表列。
  • 行号从i一直到n-1 内循环是行 j 代表行。
• 然后reserve每一行

方法二、旋转四个矩形

将给定的矩阵分成四个矩形并且将原问题划归为旋转这些矩形的问题。

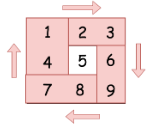
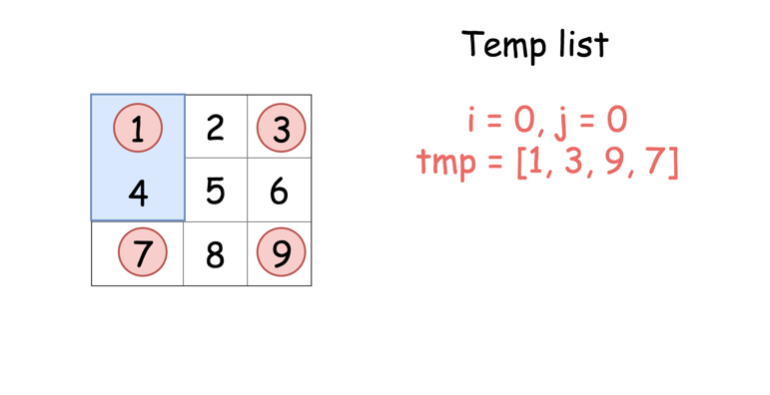
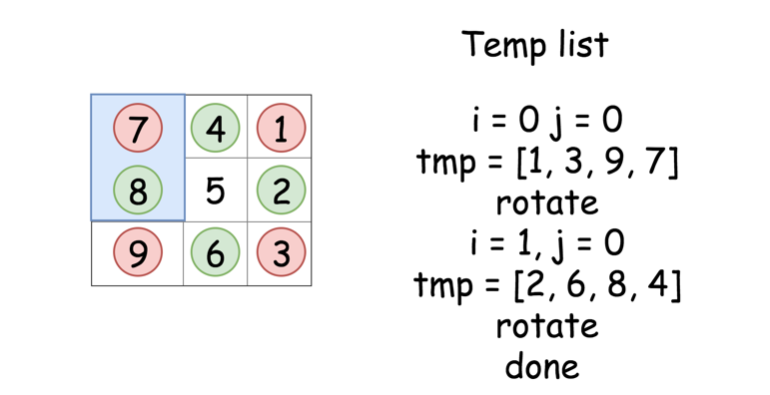
解法很直接 - 可以在第一个矩形中移动元素并且在 长度为 4 个元素的临时列表中移动它们。

算法

• 获取n的大小

• 开始外层遍历，范围是 0 - (n-2)，如果n=3，则遍历0、1两次。每次调整一组4个数字。for i in range(n // 2 + n % 2) ，外层的 i 行号。

  • 开始内存遍历，for j in range(n // 2):。

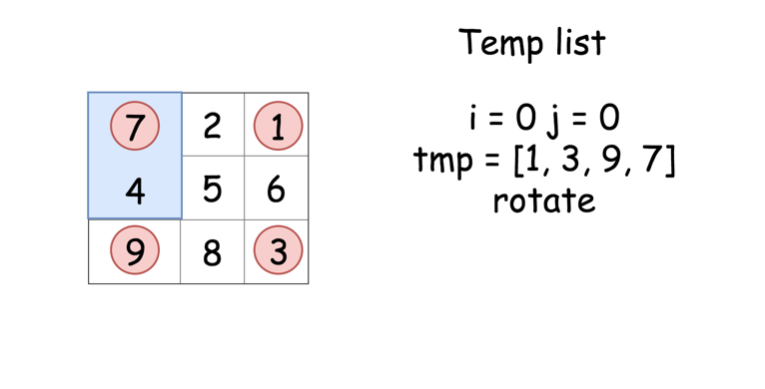
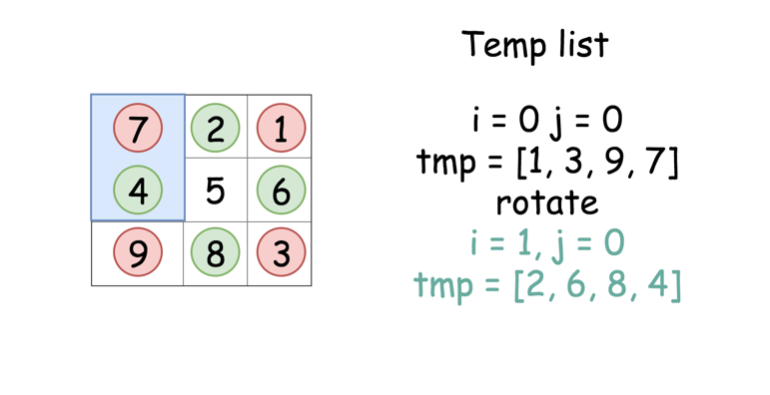
    • 先声明 tmp = [0] * 4 、row = i 、 col = j。
    • for k in range(4) 循环四次，获取四个矩形块里的值 保存在 tmp 中。注意行号和列号的切换方式 row, col = col, n - 1 - row 。
    • for k in range(4) 循环四次，利用保存在 tmp 中的结果，旋转四个矩阵块，其填充顺序是 tmp[3] 、tmp[0] 、tmp[1] 、tmp[2] ，填充方式 matrix[row][col] = tmp[(k - 1) % 4]。行列切换方式和上一步保持一致。

    k             0 1 2 3
    (k - 1) % 4   3 0 1 2

    简而言之，将整个 \(n \times n\) 的矩阵，分成了4个块，每个位置的数字，必然属于其中一个块，然后一次替换一组（4个数字），如果一个块由 \(m\) 个数字组成，就会替换 \(m\) 次，最终就完成了整个矩阵的旋转。

LeetCode官方题解

Python版本

方法一的实现

class Solution:
    def rotate(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: void Do not return anything, modify matrix in-place instead.
        """
        n = len(matrix[0])  # 获取n的大小

        # 先获得转置矩阵
        for i in range(n):  # 列号从0开始 外循环是列 i代表列
            for j in range(i, n):  # 行号从i一直到n-1 内循环是行 j代表行
                matrix[j][i], matrix[i][j] = matrix[i][j], matrix[j][i] 
        
        # reverse each row  # 然后reserve每一行
        for i in range(n):
            matrix[i].reverse()

执行用时 :56 ms, 在所有 Python3 提交中击败了16.61%的用户
内存消耗 :13.3 MB, 在所有 Python3 提交中击败了26.99%的用户
时间复杂度：\(O(N^2)\)。
空间复杂度：\(O(1)\) 由于旋转操作是 就地 完成的。

方法二的实现

class Solution:
    def rotate(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: void Do not return anything, modify matrix in-place instead.
        """
        n = len(matrix[0])  # 获取n的大小
        for i in range(n // 2 + n % 2):  # 外层遍历范围是 0-(n-2)
            for j in range(n // 2):
                tmp = [0] * 4
                row, col = i, j
                # store 4 elements in tmp
                for k in range(4):  # 获取四个块的值 保存在tmp中
                    tmp[k] = matrix[row][col]
                    row, col = col, n - 1 - row
                # rotate 4 elements   
                for k in range(4):  # 旋转四个矩阵块 填充顺序是 tmp[3]、tmp[0]、tmp[1]、tmp[2]
                    matrix[row][col] = tmp[(k - 1) % 4]  # 从tmp的后面开始往matrix[row][col]填充
                    row, col = col, n - 1 - row

执行用时 :40 ms, 在所有 Python3 提交中击败了59.48%的用户
内存消耗 :13.5 MB, 在所有 Python3 提交中击败了26.99%的用户
时间复杂度：\(O(N^2)\) 是两重循环的复杂度。
空间复杂度：\(O(1)\) 由于我们在一次循环中的操作是 就地 完成的，并且我们只用了长度为 4 的临时列表做辅助。

在单次循环中旋转 4 个矩形

class Solution:
    def rotate(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: void Do not return anything, modify matrix in-place instead.
        """
        n = len(matrix[0])        
        for i in range(n // 2 + n % 2):
            for j in range(n // 2):
                tmp = matrix[n - 1 - j][i]
                matrix[n - 1 - j][i] = matrix[n - 1 - i][n - j - 1]
                matrix[n - 1 - i][n - j - 1] = matrix[j][n - 1 -i]
                matrix[j][n - 1 - i] = matrix[i][j]
                matrix[i][j] = tmp

执行用时 :36 ms, 在所有 Python3 提交中击败了80.25%的用户。 内存消耗 :13.3 MB, 在所有 Python3 提交中击败了26.99%的用户。 时间复杂度：\(O(N^2)\) 是两重循环的复杂度。 空间复杂度：\(O(1)\) 由于旋转操作是 就地 完成的。

有效语法糖

1、Python3 快速交换两变量的值 利用此格式 a, b = b, a，可以随意交换变量值。

>>> a = 1
>>> b = 2
>>> a, b = b, a
>>> a
2
>>> b
1

>>> a = True
>>> b = "hello world"
>>> a, b = b, a
>>> a
'hello world'
>>> b
True

>>> a = 1.36
>>> b = [1, 2, 3]
>>> a, b = b, a
>>> a
[1, 2, 3]
>>> b
1.36

2、负数除法的取值

>>> -1 % 4
3