在46题的基础上添加了剪枝策略
题目
给定一个可包含重复数字的序列,返回所有不重复的全排列。
示例
示例:
| 输入: [1,1,2]
输出:
[
[1,1,2],
[1,2,1],
[2,1,1]
]
|
考察知识点
回溯算法
核心思想
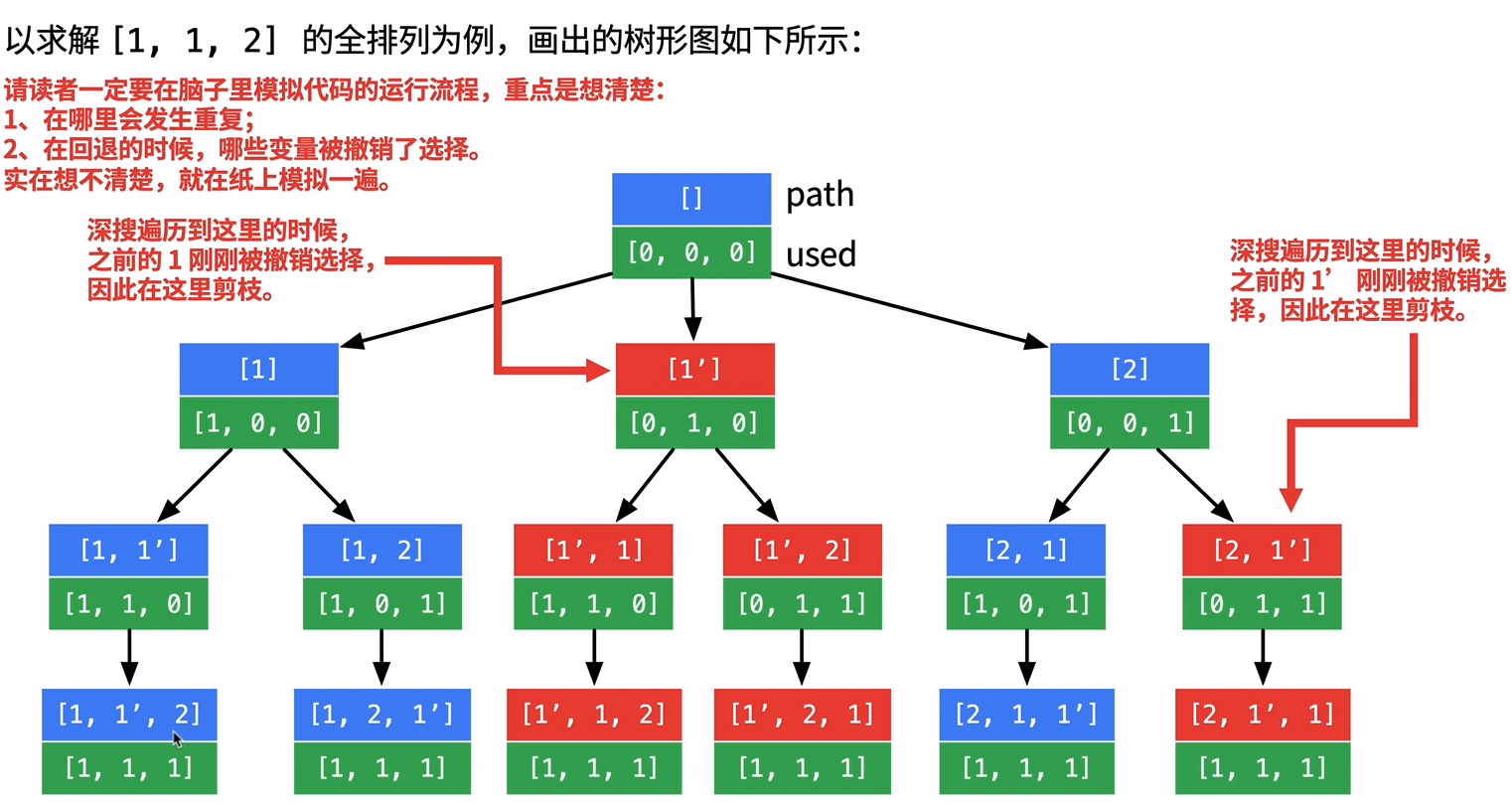
方法一、在46题的基础上,增加剪枝条件,去掉重复的。
当该节点没有被使用,且该节点和前面节点的数值一样时,这个节点就应该被剪枝跳过。
- 除了判定前后两个数必须相同以外,还要判定当前位置的前面一个位置(
index - 1 )是否被占用,因为前一个位置在回溯时肯定是先被释放了占用了的,加入 not used[i - 1] 条件,这样的剪枝更彻底。
| if index > 0 and nums[index] == nums[index -1] and (used >> (index - 1)) & 1 == 0:
continue
|
 8.png
8.png
大佬题解
Python版本
方法一的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
def backtrack(path=[], depth=0, used=0):
if depth == length:
res.append(path[:])
return
for index in range(length):
if (used >> index) & 1 == 0:
if index > 0 and nums[index] == nums[index -1] and (used >> (index - 1)) & 1 == 0:
continue
used ^= (1 << index)
path.append(nums[index])
backtrack(path, depth+1, used)
used ^= (1 << index)
path.pop()
res = []
length = len(nums)
nums.sort()
backtrack()
return res
|
时间复杂度:\(O(N \times N!)\),这里 N 为数组的长度。
空间复杂度:\(O(N \times N!)\)
执行用时 :48 ms, 在所有 Python3 提交中击败了94.50%的用户
内存消耗 :13.8 MB, 在所有 Python3 提交中击败了25.53%的用户
