LeetCode 46. 全排列（中）

本题的回溯函数，使用第一个整数的索引作为参数 backtrack(first)。
递归实现每个位置的数字都能和它后面的所有数字交换的，一共有 \(n!\) 种。

题目

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

考察知识点

回溯算法

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)  # 路径就是要添加的结果
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

核心思想

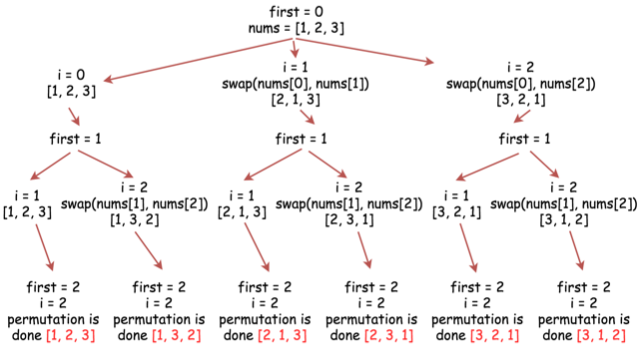
方法一、回溯法（基于递归交换）

回溯法是一种通过探索所有可能的候选解来找出所有的解的算法。如果候选解被确认不是一个解的话（或者至少不是最后一个解），回溯算法会通过在上一步进行一些变化抛弃该解，即回溯并且再次尝试。

本题的回溯函数，使用第一个整数的索引作为参数 backtrack(first)。递归实现每个位置的数字都能和它后面的所有数字交换的，一共有 \(n!\) 种。

算法

如果索引 first 等于n，意味着当前排列已完成，first 就是当前要探索的范围的开始处。
遍历索引 first 到索引 n - 1 的所有整数。
- 在排列中放置第 i 个整数，即swap(nums[first], nums)
- 继续生产从第 i 个整数开始的所有排列：backtrack(first + 1)
- 现在回溯，即通过 swap(nums[first], nums[i]) 还原。

LeetCode题解

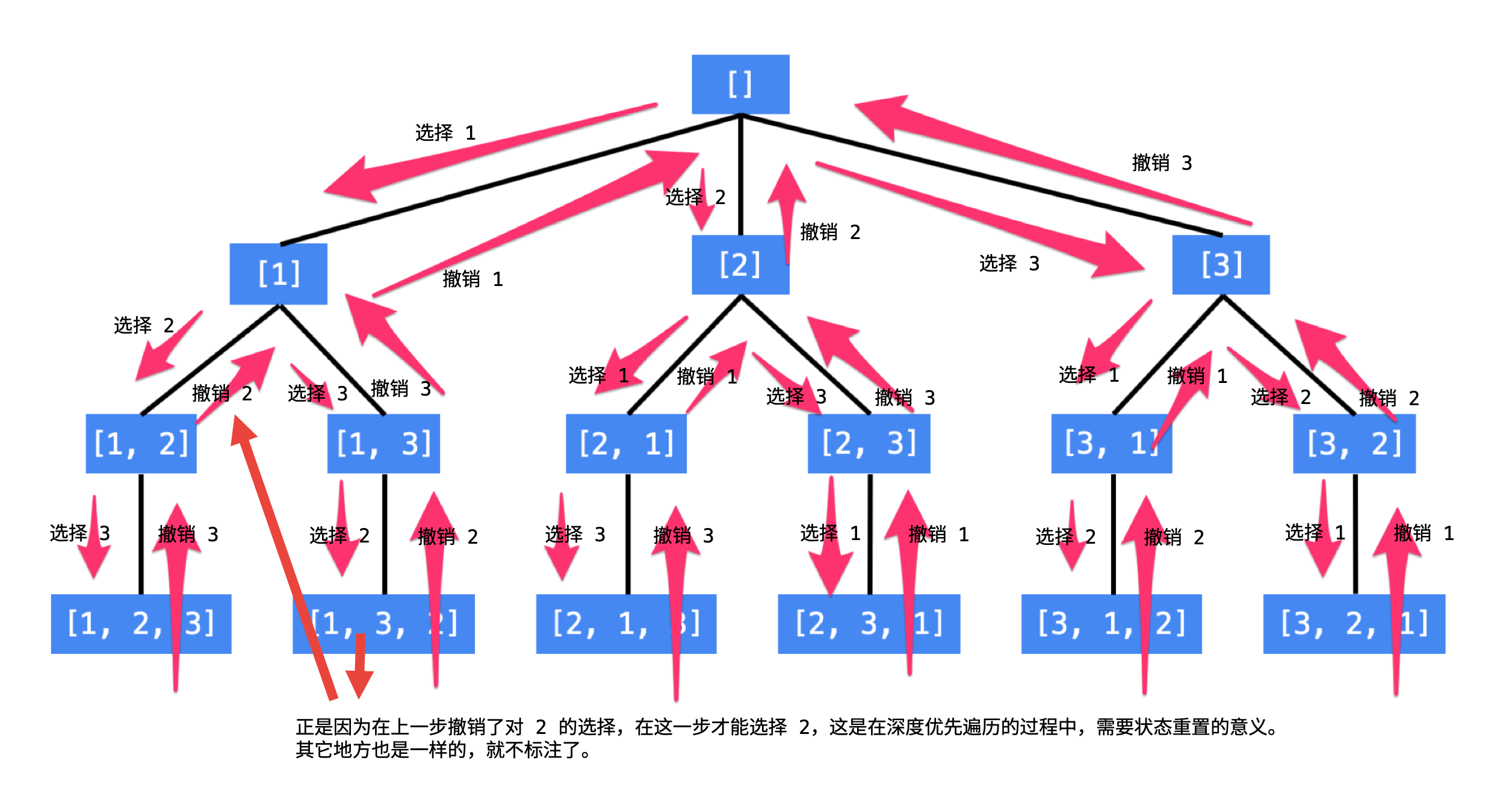
方法二、回溯算法（基于额外空间）

算法

声明 res、length、used等全局变量，其中used 用于保存每个数字的使用情况。
开始回溯
- 终止条件判断，终止条件是寻找深度达到目标深度
  - 将 path 添加到 res 中，注意，由于list是可变对象，因此，这里要用[:]取到具体的值，再append进res中。 res.append(path[:])
  - return
- 遍历所有待添加数，开始选择。
  - 如果当前数字没有使用
    - 做选择：将当前数字添加到 path 中，并更新 used 为 True。
    - 继续深度优先遍历 backtrack(path, depth + 1)
    - 撤销选择：更新 used 为 False， path 弹栈，弹出刚刚加进去的那个数字。

进一步改进

布尔数组在这题里的作用是判断某个位置上的元素是否已经使用过。有两种等价的替换方式：
（1）哈希表；
（2）位掩码，即使用一个整数表示布尔数组。此时可以将空间复杂度降到 O(1)O(1)（不包括 path 变量和 res 变量和递归栈空间消耗）。

如何使用位掩码来表示元素使用情况呢？

具体解释，可以参看本题语法糖总结部分。

大佬题解

Python版本

方法一的实现

class Solution:
    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        def backtrack(first = 0):
            # if all integers are used up
            if first == n:  
                output.append(nums[:])
            for i in range(first, n):
                # place i-th integer first 
                # in the current permutation
                nums[first], nums[i] = nums[i], nums[first]  # 每次将数与后面的一位进行交换。当交换到最后一位的时候，就将此时的解算入解集中，然后返回上层递归。
                # use next integers to complete the permutations
                backtrack(first + 1)
                # backtrack
                nums[first], nums[i] = nums[i], nums[first]
        
        n = len(nums)
        output = []
        backtrack()
        return output

方法二的实现

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        def backtrack(path=[], depth=0):  # 整个回溯函数只包含两个参数，一个是path（记录选择结果），depth（记录还剩多少没有选择）。也可以不用depth，只传递path。通过比较len(path)和len(nums)，判断是否完成寻找。回溯法就是一种深度优先遍历。
            if depth == length:  # 终止条件是寻找深度达到目标深度
                res.append(path[:])  # 由于list是可变对象，因此，这里要用[:]取到具体的值，再append进res中。
                return  # 也可以不用return，不过有return会好一点，后面逻辑在path添加到res之后就不用执行了。

            for index in range(length):  # 遍历所有待添加数
                if not used[index]:  # 如果当前数字没有使用
                    d = nums[index]  # 根据索引读取下标的操作可以放在 if 语句里面哦，只有未使用过才去读哦。
                    path.append(d)  # 添加到path
                    used[index] = True  # 更新选择情况为True代表已经被选择，以上两步就是在“进行选择”。
                    backtrack(path, depth+1)  # 继续递归回溯
                    used[index] = False  # 完成深度优先遍历（递归回溯）之后，更新选择情况为False代表还未被选择。
                    path.pop()  # 从path中弹出这一轮被选择的数字，以上两步就是在“撤销选择”。

        res = []  # 声明res、length、used等全局变量
        length = len(nums)
        used = [False] * length  # 这个解法的精髓就是使用used这个额外的存储空间保存nums的使用情况。
        backtrack()  # 开始回溯
        return res

print("leet code accept!!!")
Input = [[1, 2, 3], [1, 2, 3, 4]]
Input1 = []
Answer = [
    [
        [1,2,3],[1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]
    ],
    [
        [1, 2, 3, 4], [1, 2, 4, 3], [1, 3, 2, 4], [1, 3, 4, 2], [1, 4, 3, 2], [1, 4, 2, 3], [2, 1, 3, 4], [2, 1, 4, 3], [2, 3, 1, 4], [2, 3, 4, 1], [2, 4, 3, 1], [2, 4, 1, 3], [3, 2, 1, 4], [3, 2, 4, 1], [3, 1, 2, 4], [3, 1, 4, 2], [3, 4, 1, 2], [3, 4, 2, 1], [4, 2, 3, 1], [4, 2, 1, 3], [4, 3, 2, 1], [4, 3, 1, 2], [4, 1, 3, 2], [4, 1, 2, 3]
    ]
]

if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)):
        print("-"*50)
        reslut = solution.permute(Input[i])
        print(reslut)
        print(len(reslut))
        print(Answer[i])
        print(len(Answer[i]))

时间复杂度：\(O(N×N!)\)
空间复杂度：\(O(N×N!)\)
执行用时 :48 ms, 在所有 Python3 提交中击败了46.34%的用户
内存消耗 :13.6 MB, 在所有 Python3 提交中击败了24.90%的用户

方法二的字符掩码版本

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        def backtrack(path=[], depth=0, used=0):  # 整个回溯函数只包含两个参数，一个是path（记录选择结果），depth（记录还剩多少没有选择）。也可以不用depth，只传递path。通过比较len(path)和len(nums)，判断是否完成寻找。回溯法就是一种深度优先遍历。
            if depth == length:  # 终止条件是寻找深度达到目标深度
                res.append(path[:])  # 由于list是可变对象，因此，这里要用[:]取到具体的值，再append进res中。
                return  # 也可以不用return，不过有return会好一点，后面逻辑在path添加到res之后就不用执行了。

            for index in range(length):  # 遍历所有待添加数
                if (used >> index) & 1 == 0:  # 如果当前数字没有使用，即该位置的二进制值为0
                    d = nums[index]  # 根据索引读取下标的操作可以哦放在 if 语句里面，只有未使用过才去读哦。
                    used ^= (1 << index)  # 将该位置的二进制值从0改成1
                    path.append(d)  # 添加到path
                    backtrack(path, depth+1, used)  # 继续递归回溯
                    used ^= (1 << index)  # 将该位置的二进制值从0改成1，完成深度优先遍历（递归回溯）之后，更新选择情况为False代表还未被选择。
                    path.pop()  # 从path中弹出这一轮被选择的数字，以上两步就是在“撤销选择”。

        res = []  # 声明res、length、used等全局变量
        length = len(nums)
        backtrack()  # 开始回溯，初始时used是000。
        return res

时间复杂度：\(O(N×N!)\)
空间复杂度：\(O(N×N!)\)
执行用时 :32 ms, 在所有 Python3 提交中击败了98.16%的用户
内存消耗 :13.7 MB, 在所有 Python3 提交中击败了24.67%的用户

有效语法糖

1、使用字符掩码代替哈希表、布尔数组，记录不同元素的情况，实现空间复杂度为 \(O(1)\)。
布尔数组的表示也可以通过一个整数的二进制表示，在每个数位上非 0 即 1，这就可以表示一个布尔型数组。它们的区别仅在于：
1). 二进制右边是低位，数组左边是索引为 0 的位置；
2). 一个整数的二进制有 32 位，不过回溯搜索的问题复杂度基本上都很高，本题是 O(n!) ，n = 32 的时候已经非常大了，一般来说测试用例都达不到这个级别。

因此，完全可以用一个整数表示一个布尔型数组。而我们对布尔型数组的操作不外乎就两个：
1). 把某个索引位置从 true 变为 false。
2). 把某个索引位置从 fasle 变为 true。

异或操作，是不进位的加法，一个数位异或上 1 以后，它的功效就是使得 1 变 0 ，0 变 1。因此就可以通过对整数进行异或运算达到操作布尔型数组的效果。

'''
输入：四位数据对应的真假情况，其中只有第1位为真（从0开始）。
输出：为真的那一位的下标，也就是输出1。
'''

# 哈希表形式 空间复杂度为O(n)
>>> b = {0: False, 1: True, 2: False, 3: False}
>>> for i in b:
...     if b[i]:
...             print(i)
...
1

# 布尔数组形式 空间复杂度为O(n)
>>> a = [False, True, False, False]
>>> for i,v in enumerate(a):
...     if v:
...             print(i)
1

# 字符掩码形式 空间复杂度为O(1)
>>> c = 4  # 0100
>>> c_len = 4   # 一共要判断4个位置数据对应的情况（True or False）
>>> for i in range(c_len):  
...     if (c >> i & 1) != 0:  # 牢记这个判断条件
...             print(c_len - 1 - i)
...
1
# 当i = 0 时 c >> i & 1 => 0100 >> 0 & 1 => 0100 & 0001 = 0 == 0，该位置不是True。
# 当i = 1 时 c >> i & 1 => 0100 >> 1 & 1 => 0010 & 0001 = 0 == 0，该位置不是True。
# 当i = 2 时 c >> i & 1 => 0100 >> 2 & 1 => 0001 & 0001 = 1 != 0，该位置是True。
# 布尔数组中是从左向右第 i 位的值为True，在整型变量中，是从右向左第 i 位的值为1，代表该位置为True（这里 i 从 0 开始）。这两者是相反的，所以最后输出的位置是c_len - 1 - i

# 将c的第x位从1变成0
>>> x = 1
>>> c = 4  # 0100
>>> c_len = 4   # 一共要判断4个位置数据对应的情况（True or False）
>>> c ^= 1 << (c_len - 1 - x)  # 1 << c_len - 1 - x = 0100 / c = 0100 / 二者异或为 0000
>>> c
0  # 0000 第1位从1变成了0 0100->0000

# 将c的第x位从0变成1
>>> c = 4
>>> x = 2
>>> c_len = 4
>>> c ^= 1 << (c_len - 1 - x)
>>> c
6  # 0110 第2位从0变成了1 0100->0110

LeetCode

回溯算法

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

LeetCode 47. 全排列 II（中）上一篇

LeetCode 45. 跳跃游戏 II（难）下一篇