LeetCode 45. 跳跃游戏 II（难）

贪心算法的三个步骤

第一步、明确到底什么是最优解？
第二步、明确什么是子问题的最优解？（子问题的最优解有很多，选择一个最直接、最容易理解的方式进行定义即可。）
第三步、分别求出子问题的最优解再堆叠出全局最优解。

题目

给定一个非负整数数组，你最初位于数组的第一个位置。 数组中的每个元素代表你在该位置可以跳跃的最大长度，但是你不一定要这么跳。 你的目标是使用最少的跳跃次数到达数组的最后一个位置。

说明: 假设你总是可以到达数组的最后一个位置。

示例

示例: 

1
2
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

考察知识点

贪心算法

核心思想

方法一、贪心算法

贪心算法的三个步骤

第一步、明确到底什么是最优解？
第二步、明确什么是子问题的最优解？（子问题的最优解有很多，选择一个最直接、最容易理解的方式进行定义即可。）
第三步、分别求出子问题的最优解再堆叠出全局最优解。

本问题的三个步骤

第一步、最优解：使用最少的步数到达最后一个位置。
第二步、子问题最优解：在第i 步走最远的距离。
第三步、分别求出子问题的最优解再堆叠出全局最优解：计算每一步的结果，当累积距离等于或者超出终点时，结束运算，返回执行跳跃的次数，就是最小步数。

算法步骤

  • 定义步数 step=0，能达到的最远位置max_bound=0，和上一步到达的边界end=0。
  • 遍历数组，遍历范围 [0,n-1):
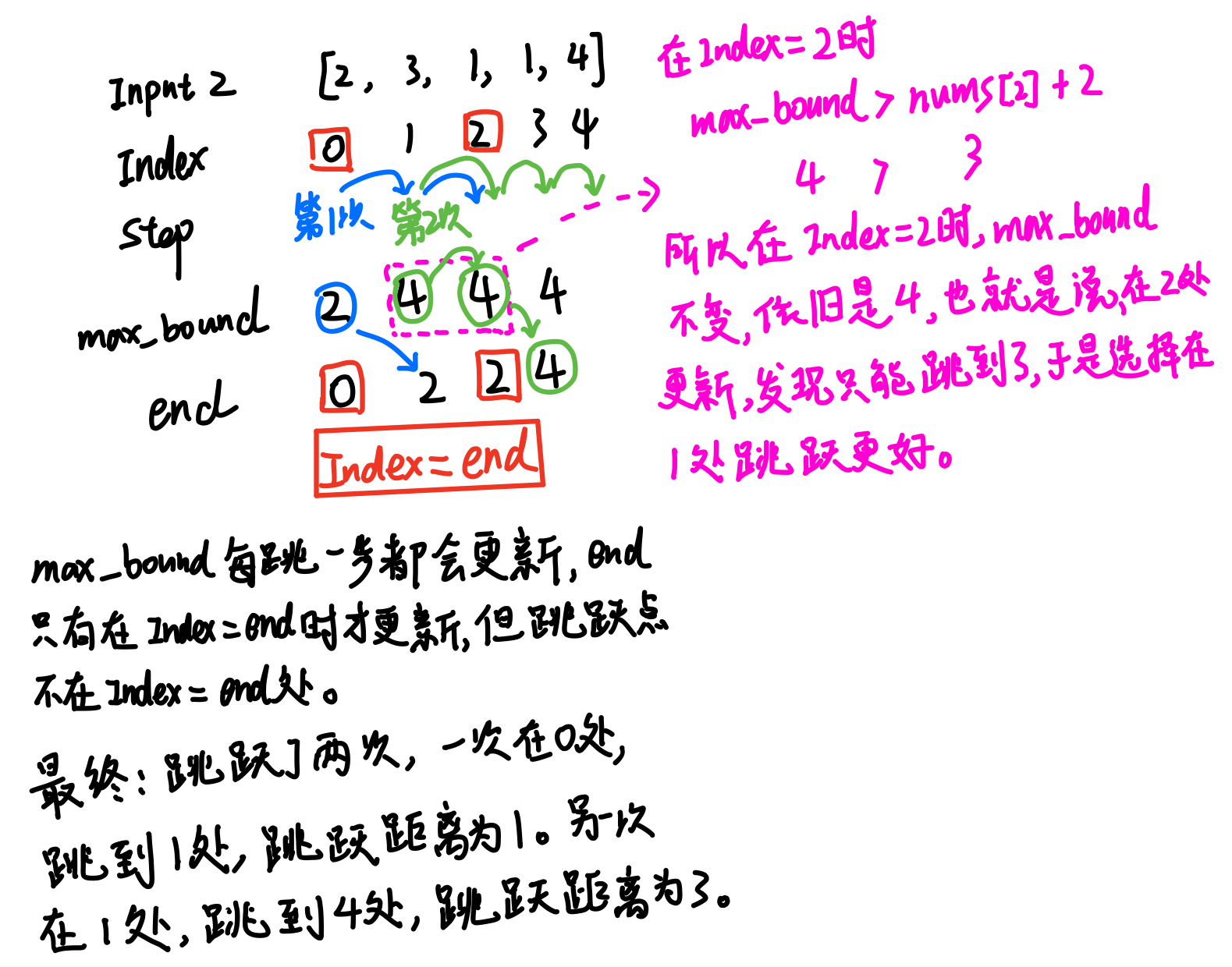
    • 所能达到的最远位置max_bound=max(max_bound,nums[i]+i) ，表示上一最远位置和当前索引 i 和索引 i 上的步数之和中的较大者，作为新的最远距离，如果上次跳跃的最远距离比在这里跳跃还远（max_bound > nums[i]+i），那就继续上次的跳跃。
    • 如果索引 i 到达了上一步的边界 end，即 i==end，则更新边界end ，令 end 等于新的最远边界max_bound，即 end=max_bound ，令步数 step 加 1。
  • 返回step 注意！ 数组遍历范围为 [0,n-1)，因为当 i==0 时，step 已经加一，所以若最后一个元素也遍历的话，当end 恰好为 n-1 ，步数会多1。

QQ图片20200304121528.jpg

大佬题解

Python版本

方法一的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution:
    def jump(self, nums: List[int]) -> int:
        step=0  # 初始化步数step、上一步的边界end、最大边界max_bound
        end=0
        max_bound=0
        ans = []
        for i in range(len(nums)-1):  # 遍历数组，遍历范围 [0,n-1)。
            max_bound=max(max_bound, nums[i]+i) # 所能达到的最远位置max_bound=max(max_bound,nums[i]+i) ，表示上一跳所能达到的最远距离max_bound和基于当前索引所能达到的最远距离，哪一个更远，选最远的那个为准，这样一来，即使下面i!=n，也能保持一个max_bound持续更新最大具体理解可以看下面输入2的例子。
            if(i==end):  # 果索引 i 到达了上一步的边界 end，即 i==end，则更新边界end ，令 end 等于新的最远边界max_bound，即 end=max_bound ，令步数 step 加一
                step+=1
                end=max_bound
                ans.append((i, max_bound))
        print(ans)
        return step


print("leet code accept!!!")
Input = [[3,4,3,2,5,4,3], [2,3,1,1,4], [1,1,1,1,1]]
Input1 = []
Answer = [3, 2, 4]

if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)):
        print("-"*50)
        reslut = solution.jump(Input[i])
        print(reslut==Answer[i])

时间复杂度：O(n)
空间复杂度：O(1)
执行用时 :52 ms, 在所有 Python3 提交中击败了97.36%的用户
内存消耗 :14.7 MB, 在所有 Python3 提交中击败了96.65%的用户

输出分析

1
2
3
4
5
6
7
8
9
10
11
输入1：[3,4,3,2,5,4,3]
跳跃点：[(0, 3), (3, 5), (5, 9)]  # 第一次在0处跳跃3次到达3处，第二次在3出跳跃两次到达5处，最后一次在5处跳跃4次到达9处（实际最大位置在6）
跳跃次数：3

输入2：[2,3,1,1,4]
跳跃点：[(0, 2), (2, 4)]  # 第一次在0处跳跃2次，达到2处之后发现，2处只能跳跃一次达到3处。但是，如果在0处跳跃1次达到1处，此时可以再跳跃3次(nums[1])，最终到达4处，这比在2处只能跳跃一次达到3处还远。所以第二次跳跃的终点在4处，但是，其实起点在1，因为只有在1处，才能跳3步到4处。
跳跃次数：2

输入3：[1,1,1,1,1]
跳跃点：[(0, 1), (1, 2), (2, 3), (3, 4)]  # 第一次在0处跳跃1次达到1处，第二次在1处跳跃1次达到2处，第一次在2处跳跃1次达到3处，第一次在3处跳跃1次达到4处。
跳跃次数：4

略作修改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def jump(self, nums: List[int]) -> int:
        step=0  # 初始化步数step、上一步的边界end、最大边界max_bound
        end=0
        max_bound=0
        length = len(nums)
        for i in range(length-1):  # 遍历数组，遍历范围 [0,n-1)。
            max_bound=max(max_bound, nums[i]+i) # 所能达到的最远位置max_bound=max(max_bound,nums[i]+i) ，表示上一跳所能达到的最远距离max_bound和基于当前索引所能达到的最远距离，哪一个更远，选最远的那个为准。
            if(i==end):  # 果索引 i 到达了上一步的边界 end，即 i==end，则更新边界end ，令 end 等于新的最远边界max_bound，即 end=max_bound ，令步数 step 加一
                step+=1
                end=max_bound
                if max_bound >= length - 1:  # 添加了一个判断，当前跳跃之后，如果已经超出了最大值，就直接break就ok了。
                    break
        return step

执行用时 :32 ms, 在所有 Python3 提交中击败了100.00%的用户
内存消耗 :14.7 MB, 在所有 Python3 提交中击败了98.23%的用户