LeetCode 44. 通配符匹配（难）

动态规划，发现两个规则，结合dp矩阵进行运算。

题目

给定一个字符串 (s) 和一个字符模式 (p) ，实现一个支持 '?' 和 '*' 的通配符匹配。

1
2
'?' 可以匹配任何单个字符。
'*' 可以匹配任意字符串（包括空字符串）。

两个字符串完全匹配才算匹配成功。

说明:

  • s 可能为空，且只包含从 a-z 的小写字母。
  • p 可能为空，且只包含从 a-z 的小写字母，以及字符 ? 和 *

示例

示例 1: 

1
2
3
4
输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

示例 2: 

1
2
3
4
输入:
s = "aa"
p = "*"
输出: true
解释: '*' 可以匹配任意字符串。

示例 3: 

1
2
3
输入:
s = "cb"
p = "?a"
输出: false 解释: '?' 可以匹配 'c', 但第二个 'a' 无法匹配 'b'。

示例 4: 

1
2
3
输入:
s = "adceb"
p = "*a*b"
输出: true 解释: 第一个 '*' 可以匹配空字符串, 第二个 '*' 可以匹配字符串 "dce".

示例 5: 

1
2
3
输入:
s = "acdcb"
p = "a*c?b"
输入: false

考察知识点

贪心算法、字符串、动态规划、回溯算法

核心思想

方法一、递归

  • 清理输入数据用一个星号代替多个星号：p = remove_duplicate_stars(p)。
  • 初始化记忆哈希表 dp。
  • 返回 helper 函数，用清理后的输入作为参数。
  • helper(s,p)：
    • 如果 (s,p) 已经计算过存储在 dp 中，则返回 dp 中的值。
    • 如果字符串相等 p == s 或 p == '*'，在 dp 添加 dp[(s, p)] = True
    • 反之如果 p 或 s 为空，则 dp[(s, p)] = False。
    • 反之如果当前字符匹配，即 p[0] == s[0] 或 p[0] == '?'，则继续检查下一个字符并 dp[(s, p)] helper(s[1:], p[1:])。
    • 反之如果当前字符模式是一个星号 p[0] == '*'，则有两种情况，要么不匹配字符要么匹配一个或多个字符，则 dp[(s, p)] = helper(s, p[1:]) or helper(s, p[1:])。
    • 反之如果 p[0] != s[0]，则 dp[(s, p)] = False。
    • 返回 dp[(s, p)]。

方法二、动态规划（发现两个规则，结合dp矩阵进行运算。）

将问题简化为简单的问题，例如，有一个字符串 \(adcebdk\) 和字符模式 \(\*a\*b?k\) ，计算是否匹配 D = True/False。我们将输入字符串和字符模式的长度 p_len，s_len 和是否匹配 D[p_len][s_len] 联系起来。

让我们进一步介绍 D[p_idx][s_idx]，D[p_idx][s_idx] 代表的是字符模式中的第 p_idx 字符和输入字符串的第 s_idx 字符是否匹配。

规则一、字符相同或字符模式的字符为 ?，则有 D[p_idx][s_idx]=D[p_idx - 1][s_idx - 1]

8.png

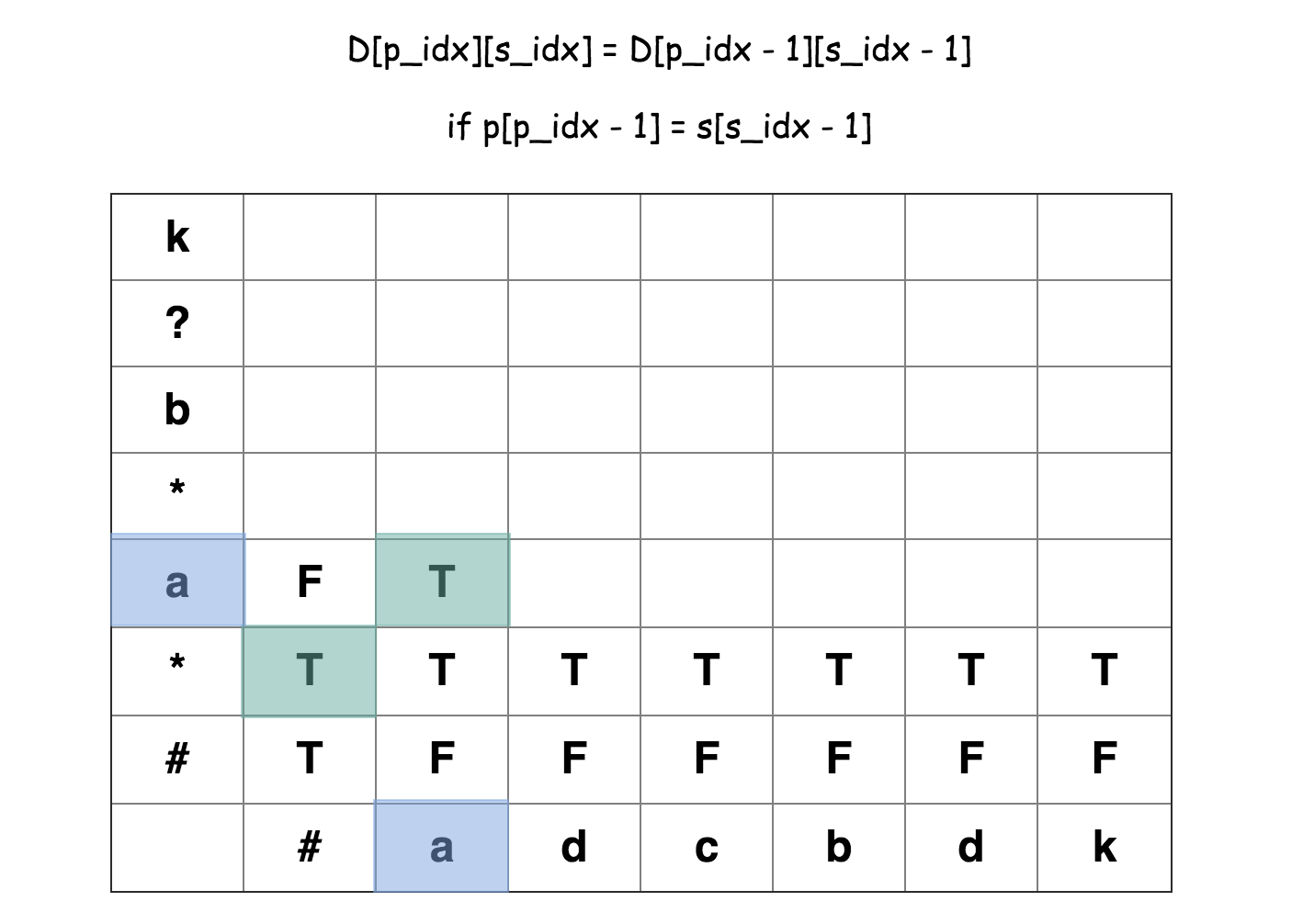
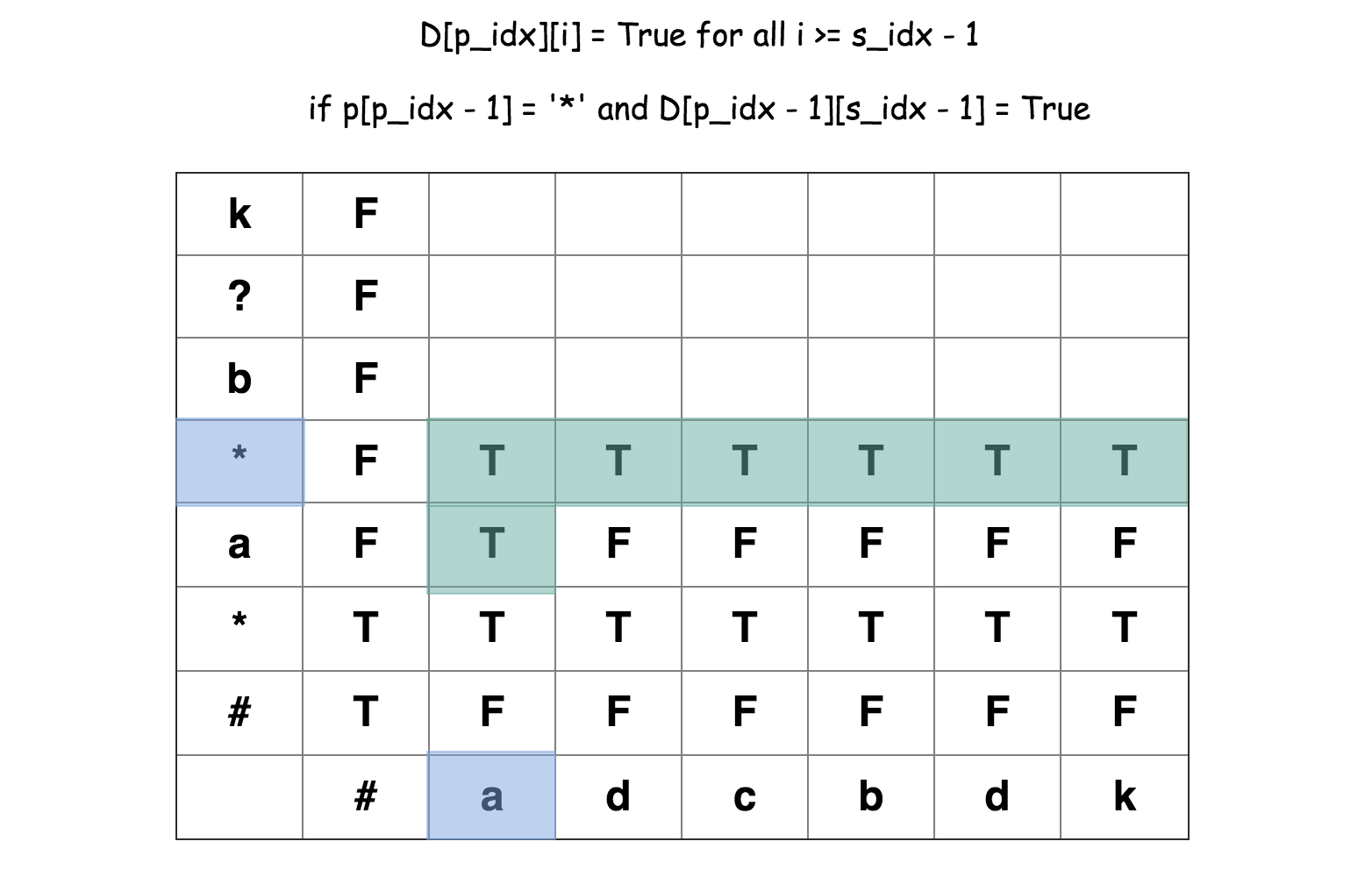
规则二、字符模式的字符为*且 D[p_idx - 1][s_idx - 1] = True，则有：
- 星号匹配完成。 - 星号继续匹配更多的字符。

即：D[p_idx - 1][i] = True, i >= s_idx - 1

9.png

所以，每一步的计算是基于之前完成的计算完成的。

算法

初始化匹配表为 False 除了D[0][0] = True。 使用规则 1 和规则 2 计算表格，最后返回 D[p_len][s_len] 作为答案。

方法三、回溯法

复杂度 \(O(SP)\) 比 \(O(2^{\min(S, P/2)})\) 好的多，但是仍然有改进的余地。不需要计算整个表格，也就是检查每个星号的所有可能性：

匹配 0 个字符。 匹配 1 个字符。 匹配 2 个字符。

---

匹配剩余所有字符

核心思想就是：我们从匹配 0 个字符开始，如果这个假设导致不匹配，则回溯：回到前一个星号，假设它匹配一个字符，然后继续。若又是不匹配的情况？再次回溯：回到上一个星号，假设匹配两个字符，等等。

10.png

算法：

我们使用两个指针：s_idx 遍历输入字符串，p_idx 遍历字符模式。当 s_idx < s_len： - 如果字符模式仍有字符 p_idx < p_len 且指针下的字符匹配 p[p_idx] == s[s_idx] 或 p[p_idx] == '?'，则两个指针向前移动。 - 反之如果字符模式仍有字符 p_idx < p_len 且 p[p_idx] == '*'，则首先检查匹配 0 字符的情况，即只增加模式指针 p_idx++。记下可能回溯的位置 star_idx 和当前字符串的位置 s_tmp_idx。 - 反之如果出现不匹配的情况： - 如果字符模式中没有星号，则返回 False。 - 如果有星号，则回溯：设置 p_idx = star_idx + 1 和 s_idx = s_tmp_idx + 1，假设这次的星匹配多个字符。则可能的回溯为 s_tmp_idx = s_idx。 - 如果字符模式的所有剩余字符都是星号，则返回 True。

代码步骤

1、声明s_len、p_len、s_idx、p_idx、star_idx、s_tmp_idx等变量
2、开始while循环，循环在s_idx等于s_len的时候结束，也就string指针指到最后一位的时候结束。
2.1、如果字符模式仍有字符 p_idx < p_len 且指针下的字符匹配 p[p_idx] == s[s_idx] 或 p[p_idx] == '?'，则两个指针向前移动。
2.2、反之如果字符模式仍有字符 p_idx < p_len 且 p[p_idx] == '*'，则首先检查匹配 0 字符的情况，即只增加模式指针 p_idx++。记下可能回溯的位置 star_idx 和当前字符串的位置 s_tmp_idx。
2.3、反之如果如果字符模式中没有星号也不匹配，则直接返回 False。
2.4、不满足前面所有判断，说明当前没能匹配上，但是star_index != -1，也就是存在*，则回溯，让*匹配更多string中的字符：设置 p_idx = star_idx + 1 和 s_idx = s_tmp_idx + 1，假设这次的星匹配多个字符。则可能的回溯为 s_tmp_idx = s_idx。
3、结束while循环，如果字符模式的所有剩余字符都是星号，则返回 True。

LeetCode题解

Python版

方法一的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution:
    def remove_duplicate_stars(self, p):
        if p == '':
            return p
        p1 = [p[0],]
        for x in p[1:]:
            if p1[-1] != '*' or p1[-1] == '*' and x != '*':
                p1.append(x)
        return ''.join(p1) 
        
    def helper(self, s, p):
        dp = self.dp
        if (s, p) in dp:
            return dp[(s, p)]

        # 这里考虑了所以的情况
        if p == s or p == '*':
            dp[(s, p)] = True
        elif p == '' or s == '':
            dp[(s, p)] = False
        elif p[0] == s[0] or p[0] == '?':
            dp[(s, p)] = self.helper(s[1:], p[1:])
        elif p[0] == '*':
            dp[(s, p)] = self.helper(s, p[1:]) or self.helper(s[1:], p)
        else:
            dp[(s, p)] = False

        return dp[(s, p)]
        
    def isMatch(self, s, p):
        p = self.remove_duplicate_stars(p)
        # memorization hashmap to be used during the recursion
        self.dp = {}
        return self.helper(s, p)

时间复杂度：最好的情况下 \(O(min(S,P))\)，最坏的情况下是 \(O(2^{min(S,P/2)})\)。其中 S 和 P 指的是输入字符串和字符模式的长度。 最好的情况很明显，让我们估算最坏的情况。最耗时的递归是字符模式上的星号形成树的情况，将执行两个分支 helper(s, p[1:]) 和 helper(s[1:], p)。数据清理后字符模式中的最大星树为 \(P/2\)，因此时间复杂度： \(O(2^{min(S,P/2)} )\)。
空间复杂度：\(O(2^{min(S,P/2)})\)，用来存储记忆哈希表和递归调用堆栈。
执行用时：1136 ms, 在所有 Python3 提交中击败了21.59%的用户
内存消耗：663.8 MB, 在所有 Python3 提交中击败了5.20%的用户

方法二的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution:
    def isMatch(self, s, p):
        s_len = len(s)
        p_len = len(p)
        
        # basic cases 特判
        if p == s or p == '*':
            return True
        if p == '' or s == '':
            return False
        
        # init all matrix except [0][0] element as False 
        # 声明保存中间结果的矩阵 d
        d = [ [False] * (s_len + 1) for _ in range(p_len + 1)]
        d[0][0] = True
        
        # DP compute 开始动态规划算法
        for p_idx in range(1, p_len + 1):
            # 规则二、匹配字符为*
            if p[p_idx - 1] == '*':  # 当前的Pattern的字符为* 且 D[p_idx - 1][s_idx - 1] = True
                s_idx = 1
                # 只要d[p_idx - 1][s_idx - 1]为False同时s_idx还小于s_len + 1，就通过s_idx自增，找到第一个string中的、可以匹配的字符。
                while not d[p_idx - 1][s_idx - 1] and s_idx < s_len + 1:
                    s_idx += 1
                # 如果 pattern 匹配 string，d[p_idx - 1][s_idx - 1] = True，这时先更新d[p_idx][s_idx - 1]。
                d[p_idx][s_idx - 1] = d[p_idx - 1][s_idx - 1]
                
                # 再继续基于星号，匹配更多的字符。
                while s_idx < s_len + 1:
                    d[p_idx][s_idx] = True
                    s_idx += 1

            # 规则一、字符相同或字符模式的字符为 `?`
            elif p[p_idx - 1] == '?':
                for s_idx in range(1, s_len + 1): 
                    d[p_idx][s_idx] = d[p_idx - 1][s_idx - 1] 
            else:  # 最后一种情况，当前Pattern中的字符既不是"*"，也不是"?"，那就是普通的字符。
                for s_idx in range(1, s_len + 1):
                    d[p_idx][s_idx] = d[p_idx - 1][s_idx - 1] and p[p_idx - 1] == s[s_idx - 1]  # 只有d[p_idx - 1][s_idx - 1]为True，且当前字符也一样的情况下（p[p_idx - 1] == s[s_idx - 1]），才能认为是匹配成功的。

        return d[p_len][s_len]

时间复杂度：\(O(SP)\)，其中 S 和 P 指的是字符模式和输入字符串的长度。
空间复杂度：\(O(SP)\)，用来存储匹配表格。
执行用时 :472 ms, 在所有 Python3 提交中击败了78.11%的用户。
内存消耗 :21.5 MB, 在所有 Python3 提交中击败了52.60%的用户。

方法三的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution2:
    def isMatch(self, s, p):
        """
        :type s: str
        :type p: str
        :rtype: bool
        """
        # 声明s_len、p_len、s_idx、p_idx、star_idx、s_tmp_idx等变量
        s_len, p_len = len(s), len(p)  # string、pattern长度
        s_idx = p_idx = 0  # 字符串和匹配串的指针
        star_idx = s_tmp_idx = -1  # star_idx为可能的回溯位置，s_tmp_idx为当前字符串的位置。

        while s_idx < s_len:  # 循环在s_idx等于s_len的时候结束，也就string指针指到最后一位的时候结束。
            if p_idx < p_len and p[p_idx] in ['?', s[s_idx]]:  # 如果字符模式仍有字符 p_idx < p_len 且指针下的字符匹配 p[p_idx] == s[s_idx] 或 p[p_idx] == '?'，则两个指针向前移动。
                s_idx += 1
                p_idx += 1
            elif p_idx < p_len and p[p_idx] == '*':  # 反之如果字符模式仍有字符 p_idx < p_len 且 p[p_idx] == '*'，则首先检查匹配 0 字符的情况，即只增加模式指针 p_idx++。记下可能回溯的位置 star_idx 和当前字符串的位置 s_tmp_idx。
                star_idx = p_idx  # 发现了* 就更新star_index记录星号的位置。
                s_tmp_idx = s_idx
                p_idx += 1
            elif star_idx == -1:  # 反之如果如果字符模式中没有星号也不匹配，则直接返回 False。
                return False
            else:  # 不满足前面所有判断，说明当前没能匹配上，但是star_index != -1，也就是存在*，则回溯，让*匹配更多string中的字符：设置 p_idx = star_idx + 1 和 s_idx = s_tmp_idx + 1，假设这次的星匹配多个字符。则可能的回溯为 s_tmp_idx = s_idx。
                p_idx = star_idx + 1  # p_idx在star_idx的基础上后移，意味着用*匹配更多string字符。
                s_idx = s_tmp_idx + 1
                s_tmp_idx = s_idx  # 更新string可能的回溯位置
        
        # The remaining characters in the pattern should all be '*' characters
        return all(x == '*' for x in p[p_idx:])  # 结束while循环，如果字符模式（Pattern）的所有剩余字符都是星号，则返回 True。

时间复杂度：最好的情况下是 \(O(min(S,P))\)，平均情况下是 \(O(S \log P)\)，其中 S 和 P 指的是字符模式和输入字符串的长度。详细证明可点击：证明过程。
空间复杂度：\(O(1)\)。
执行用时 :84 ms, 在所有 Python3 提交中击败了82.88%的用户。
内存消耗 :13.5 MB, 在所有 Python3 提交中击败了87.95%的用户。

有效语法糖

1、all() 函数，当可迭代对象（list、set）中全为真值时，返回 True。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
>>> a = [False, False]
>>> a
[False, False]
>>> all(a)
False
>>> a = [True, False]
>>> all(a)
False
>>> a = [True, True]
>>> all(a)
True
>>> b = (False, False)
>>> type(b)
<class 'tuple'>
>>> all(b)
False
>>> b = (False, True)
>>> all(b)
False
>>> b = (True, True)
>>> all(b)
True
>>> c = {"1": False, "2": False}
>>> type(c)
<class 'dict'>
>>> all(c)
True

2、一种更加简洁的if条件写法

1
2
3
if p_idx < p_len and p[p_idx] in [s[s_idx], "*"]:
# 等效于
if p_idx < p_len and (p[p_idx] == s[s_idx or p[p_idx] == "*"):