LeetCode 42. 接雨水（难）

用栈来跟踪可能储水的最长的条形块。使用栈就可以在一次遍历内完成计算。我们在遍历数组时维护一个栈。如果当前的条形块小于或等于栈顶的条形块，我们将条形块的索引入栈，意思是当前的条形块被栈中的前一个条形块界定。如果我们发现一个条形块长于栈顶，我们可以确定栈顶的条形块被当前条形块和栈的前一个条形块界定，因此我们可以弹出栈顶元素并且累加答案到 ans 。

题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。感谢 Marcos 贡献此图。

示例

1 2	`输入: [0,1,0,2,1,0,1,3,2,1,2,1] 输出: 6`

考察知识点

栈、数组、双指针

做这个题的关键，是要知道，一个位置的积水量，是左边最大边界和右边最大边界中较小的那一个，乘以宽度，或者减去当前位置高度，来计算得到的。

核心思想

方法一、暴力破解法

1 2	`index [0,1,2,3,4,5,6,7,8,9,10,11] value [0,1,0,2,1,0,1,3,2,1,2,1]`

直观想法 直接按问题描述进行。对于数组中的每个元素，我们找出下雨后水能达到的最高位置，等于两边最大高度的较小值减去当前高度的值。以index=2为例，其两边最大高度分别是height[1]=1和height[3]=2，这二者中的较小值是height[1]=1，当前值height[2]=0，所以可以接到水滴的个数为1=height[1]-height[0]。

算法

初始化 ans=0
从左向右扫描数组：
- 初始化 $\text{max_left}=0$ 和 $\text{max_right}=0$
- 从当前元素向左扫描并更新：
  - $\text{max_left}=\max(\text{max_left}, \text{height}[j])$
- 从当前元素向右扫描并更新：
  - $\text{max_right}=\max(\text{max_right}, \text{height}[j])$
- 将$\min(\text{max_left},\text{max_right}) - \text{height}[i]$累加到 $\text{ans}$

方法二、动态规划

在暴力破解的基础上，将最大值保存起来，动态规划的最显著特点就是将之前的计算结果进行保存，避免重复计算。

直观想法

在暴力方法中，我们仅仅为了找到最大值每次都要向左和向右扫描一次。但是我们可以提前存储这个值。因此，可以通过动态编程解决。

关键代码

while i < length:
    left_max[i] = max(height[i], left_max[i - 1])
    i += 1
while i >= 0:
    right_max[i] = max(height[i], right_max[i + 1])
    i -= 1

这个概念可以见下图解释：

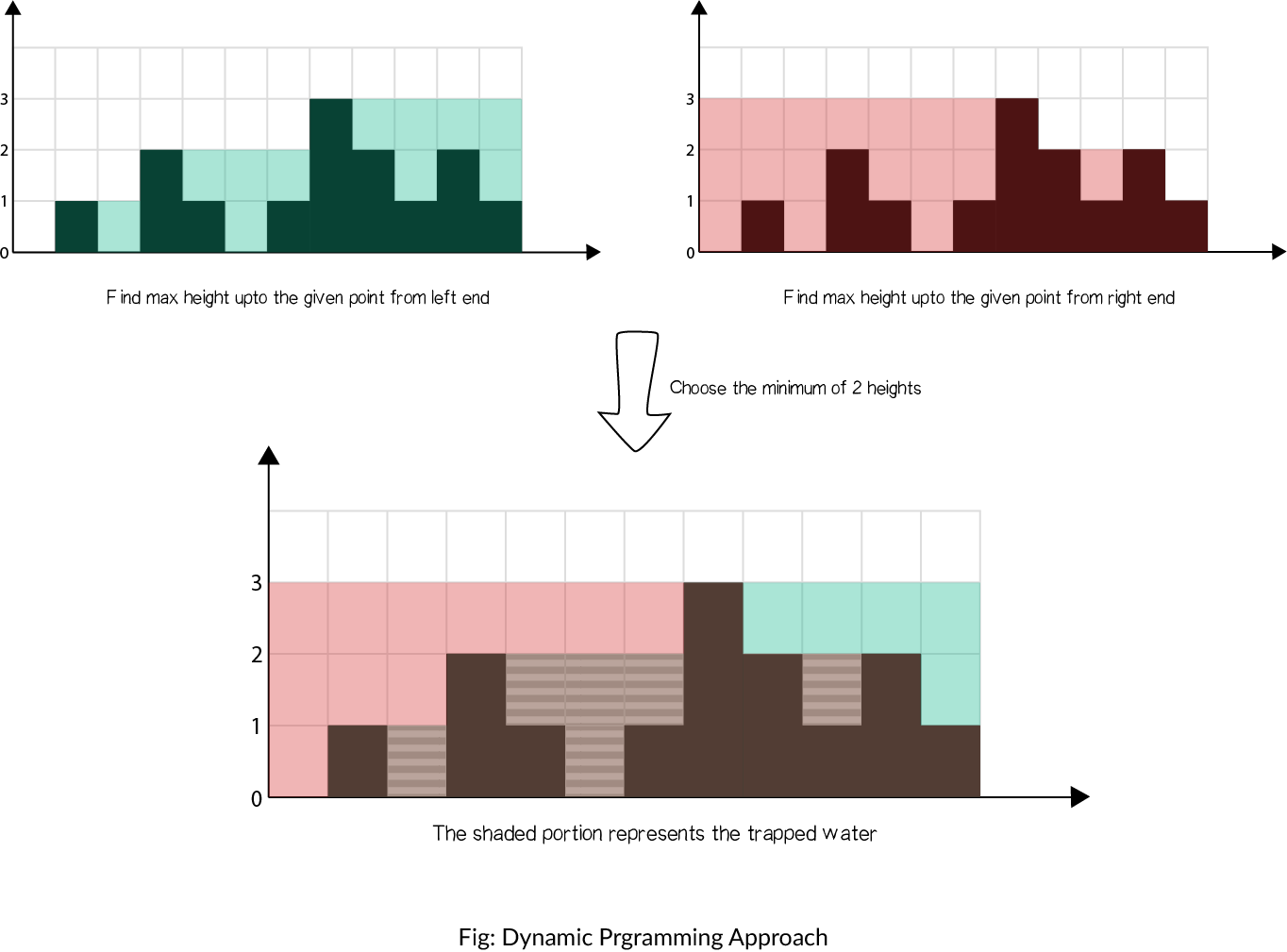
代码步骤
1、特判height为空的情况，直接返回0。
2、声明ans、left_max、right_max等变量。
3、从左往右边寻找每个位置的left_max。
4、从右往左寻找每个位置的right_max。
5、利用left_max和right_max计算容量。

方法三、使用栈实现计算

直观想法

我们可以不用像方法 2 那样存储最大高度，而是用栈来跟踪可能储水的最长的条形块。使用栈就可以在一次遍历内完成计算。

我们在遍历数组时维护一个栈。如果当前的条形块小于或等于栈顶的条形块，我们将条形块的索引入栈，意思是当前的条形块被栈中的前一个条形块界定。如果我们发现一个条形块长于栈顶，我们可以确定栈顶的条形块被当前条形块和栈的前一个条形块界定，因此我们可以弹出栈顶元素并且累加答案到 ans 。

算法

使用栈来存储条形块的索引下标。
遍历数组：
- 当栈非空且 $\text{height}[current]>\text{height}[st.top()]$
  - 意味着栈中元素可以被弹出。弹出栈顶元素 $\text{top}$。
  - 计算当前元素和栈顶元素的距离，准备进行填充操作 $\text{distance} = \text{current} - \text{st.top}() - 1$
  - 找出界定高度 $\text{bounded_height} = \min(\text{height[current]}, \text{height[st.top()]}) - \text{height[top]}$
  - 往答案中累加积水量 $\text{ans} \mathrel{+}= \text{distance} \times \text{bounded_height}$
- 将当前索引下标入栈
- 将 $\text{current}$ 移动到下个位置

方法四、双指针

直观想法

和方法 2 相比，我们不从左和从右分开计算，我们想办法一次完成遍历。
从动态编程方法的示意图中我们注意到，只要 $ [i]>[i]$（元素 0 到元素 6），积水高度将由 $left\_{max}$ 决定，类似地 $\text{left_max}[i]>\text{right_max}[i]$（元素 8 到元素 11）。
所以我们可以认为如果一端有更高的条形块（例如右端），积水的高度依赖于当前方向的高度（从左到右）。当我们发现另一侧（右侧）的条形块高度不是最高的，我们则开始从相反的方向遍历（从右到左）。
我们必须在遍历时维护 $\text{left_max}$ 和 $\text{right_max}$ ，但是我们现在可以使用两个指针交替进行，实现 1 次遍历即可完成。

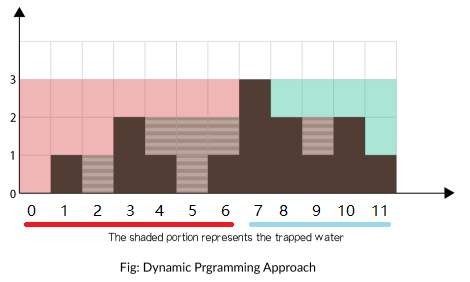
算法

初始化 left 指针为 0 并且 right 指针为 length-1
While left<right, do
- if height[left] < height[right] 满足该条件，即，left更小，以left为有效bound_height。
  - if height[left] >= left_max 更新 left_max
  - else 累加 left_max - height[left] 到 ans 每次就计算一个位置对应能够积累的水珠就行了。
  - left = left + 1
- else 否则right更小，以right为有效bound_height。
  - if height[right] >= right_max，更新 right_max
  - else 累加 right_max - height[right] 到 ans
  - right= right - 1

LeetCode 题解

Python版本

方法一的实现

class Solution:
    def trap(self, height: List[int]) -> int:
        ans = 0
        length = len(height)
        i = 1
        while i < length - 1:  
            max_left, max_right = 0, 0
            j = i
            while j >= 0:  # 寻找i位置左边最大bound
                max_left = max(max_left, height[j])
                j -= 1  # j一个一个的减到0
            j = i
            while j < length:  # 寻找i位置右边最大bound
                max_right = max(max_right, height[j])
                j += 1  # j一个一个的加到length
            ans += min(max_left, max_right) - height[i]
            i += 1
        return ans

时间复杂度： $O(n^2)$。数组中的每个元素都需要向左向右扫描。
空间复杂度 $O(1)$ 的额外空间。
通过测试用例314 / 315 个，最后一个用例，长度为10732，未能通过。

方法二的实现

class Solution:
    def trap(self, height: List[int]) -> int:
        length = len(height)
        if length == 0:  # 特判height为空的情况，直接返回0。
            return 0

        ans = 0  # 声明ans、left_max、right_max等变量
        left_max = [0] * length
        right_max = [0] * length

        # 从左往右边寻找每个位置的left_max
        left_max[0] = height[0]
        i = 1
        while i < length:
            left_max[i] = max(height[i], left_max[i - 1])
            i += 1
        
        # 从右往左寻找每个位置的right_max
        right_max[length - 1] = height[length - 1]
        i = length - 2
        while i >= 0:
            right_max[i] = max(height[i], right_max[i + 1])
            i -= 1

        # 利用left_max和right_max计算容量
        i = 1
        while i < length - 1:
            ans += min(left_max[i], right_max[i]) - height[i]
            i += 1

        return ans

时间复杂度：$O(n)$，存储最大高度数组，需要两次遍历，每次 $O(n)$ 。最终使用存储的数据更新$\text{ans}$ ，$O(n)$。
空间复杂度：$O(n)$ ，额外空间。和方法 1 相比使用了额外的 $O(n)$ 空间用来放置$\text{left_max}$ 和 $\text{right_max}$ 数组。
执行用时 :80 ms, 在所有 Python3 提交中击败了26.42%的用户
内存消耗 :13.9 MB, 在所有 Python3 提交中击败了28.11%的用户

方法三实现

class Solution:
    def trap(self, height: List[int]) -> int:
        ans, current = 0, 0  # 声明ans、current变量来保存结果和游标位置
        st = []  # st里面保存的是位置下标
        length = len(height)
        while current < length:
            while len(st) and height[current] > height[st[-1]]:  # 当st不为空且当前条块高度大于st中最后一个下标所对应条块的高度时，就形成了一个洼地，可以计算洼地存雨多少了。
                top = st[-1]  # 先获得中间条块的下标
                st.pop()  # 再弹出中间条块，这时st[-1]所对应的条块，就变成了洼地的左边界。
                if len(st) == 0:  # 如果st为空了，说明这个洼地计算完成了。
                    break
                distance = current - st[-1] - 1  # 计算底边
                bound_height = min(height[current], height[st[-1]]) - height[top]  # bound_height可能为0，只有st通过pop回退到一定位置（也就是不断左移左边界），才能有min(height[current], height[st[-1]])>height[top]，此时才能得到一个有效的bound_height。而distance也会因为st通过pop回退到一定位置（也就是不断左移左边界）而变大。
                ans += distance * bound_height  # ans可以会因为bound_height为0而为0。当bound_height有效时，ans也会最终加上一个有效值。
            st.append(current)  # 把当前最新下标保存进去
            current += 1  # 先保存再自增

        return ans

时间复杂度：$O(n)$。单次遍历 $O(n)$ ，每个条形块最多访问两次（由于栈的弹入和弹出），并且弹入和弹出栈都是 $O(1)$ 的。
空间复杂度：$O(n)$。栈最多在阶梯型或平坦型条形块结构中占用 $O(n)$ 的空间。
执行用时 :64 ms, 在所有 Python3 提交中击败了52.06%的用户
内存消耗 :14 MB, 在所有 Python3 提交中击败了28.11%的用户

方法四实现

class Solution:
    def trap(self, height: List[int]) -> int:
        ans, left, right = 0, 0, len(height) - 1
        left_max, right_max = 0, 0
        while left < right:
            if height[left] < height[right]:  # 满足该条件，即，left更小，以left为有效bound_height。
                if height[left] >= left_max:
                    left_max = height[left]
                else:
                    ans += (left_max - height[left])  # 每次就计算一个位置对应能够积累的水珠数量就行了。
                left += 1
            else:  # 否则right更小，以right为有效bound_height。
                if height[right] >= right_max:  # 
                    right_max = height[right]
                else:
                    ans += (right_max - height[right])  # 同样，只用计算一个位置对应能够积累的水珠数量。
                right -= 1
        return ans

时间复杂度：$O(n)$，单次遍历的时间O(n)。
空间复杂度：$O(1)$ ，left, right, left_max 和 ight_max 只需要常数的空间。
执行用时 :32 ms, 在所有 Python3 提交中击败了99.55%的用户
内存消耗 :13.8 MB, 在所有 Python3 提交中击败了28.30%的用户

LeetCode

栈和队列

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

LeetCode 43. 字符串相乘（中）上一篇

LeetCode 41. 缺失的第一个正数（难）下一篇