LeetCode 11. 盛最多水的容器（中）

利用双指针不停的消状态，其实质就是在移动的过程中不断消去不可能成为最大值的状态。具体如何消去，关键是要认识到“向内收窄短板可以获取面积最大值”的规律。

题目

给定 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

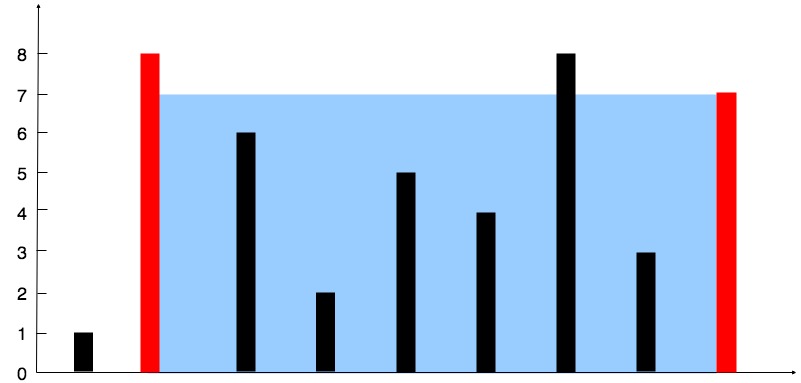
question_11.jpg

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例

1
2
输入：[1,8,6,2,5,4,8,3,7]
输出：49

考察知识点

双指针

核心思想

利用双指针不停的消状态，其实质就是在移动的过程中不断消去不可能成为最大值的状态。具体如何消去，主要是认识到以下规律。

指针移动规则与证明：

每次选定围成水槽两板高度\(h[i]\), \(h[j]\) 中的短板，向中间收窄 1 格。以下证明：

  • 设每一状态下水槽面积为 \(S(i, j) (0 <= i < j < n)\)，由于水槽的实际高度由两板中的短板决定，则可得面积公式\(S(i, j) = min(h[i], h[j]) × (j - i)\)。
  • 在每一个状态下，无论长板或短板收窄 1 格，都会导致水槽 底边宽度 -1：
    • 若向内移动短板，水槽的短板 \(min(h[i], h[j])\) 可能变大，因此水槽面积 \(S(i, j)\) 可能增大。
    • 若向内移动长板，水槽的短板 $ min(h[i], h[j])$ 不变或变小，下个水槽的面积一定小于当前水槽面积
  • 因此，向内收窄短板可以获取面积最大值。

时间复杂度 \(O(N)\)，双指针遍历一次底边宽度 N 。 空间复杂度 \(O(1)\)，指针使用常数额外空间。

LeetCode题解

Python版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# coding: utf-8

class Solution(object):
    def maxArea(self, height: list) -> int:
        i, j, max_area = 0, len(height)-1, 0
        while i < j:
            if height[i] < height[j]:
                tmp_area = height[i] * (j - i)
                if tmp_area > max_area:
                    max_area = tmp_area
                i += 1
            else:
                tmp_area = height[j] * (j - i)
                if tmp_area > max_area:
                    max_area = tmp_area
                j -= 1
        return max_area 

print("leet code accept!!!")
Input = [[1,8,6,2,5,4,8,3,7]]
Answer = [49]

if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)):
        print("-"*50)
        result = solution.maxArea(Input[i])
        # print(result)
        print(result==Answer[i])