LeetCode 41. 缺失的第一个正数（难）

一致输入数组长度为 n ，那么，大于 n 的数字，就肯定不是未出现的最小正整数。现在我们有一个只包含正数的数组，范围为 1 到 n，现在的问题是在 \(O(N)\) 的时间和常数空间内找出首次缺失的正数。如果可以使用哈希表，且哈希表的映射是 正数 -> 是否存在 的话，这其实很简单。"脏工作环境" 的解决方法是将一个字符串 hash_str 分配 n 个 0，并且用类似于哈希表的方法，如果在数组中出现数字 i 则将字符串中 hash_str[i] 修改为 1 。

题目

给定一个未排序的整数数组，找出其中没有出现的最小的正整数。 你的算法的时间复杂度应为O(n)，并且只能使用常数级别的空间。

官方提示： 1、Think about how you would solve the problem in non-constant space. Can you apply that logic to the existing space?
2、We don't care about duplicates or non-positive integers.
3、Remember that O(2n) = O(n)

示例

示例 1: 

1
2
输入: [1,2,0]
输出: 3
示例 2: 
1
2
输入: [3,4,-1,1]
输出: 2
示例 3: 
1
2
输入: [7,8,9,11,12]
输出: 1

考察知识点

数组、hash map、布隆过滤

这道题的巧妙之处在于先通过预处理排除了不可能的情况，在通过使用输入的nums数组自己构建hash map完成了只能使用常数级别额外空间的要求。

核心思想

方法一、以hash map为索引

题目特点

一致输入数组长度为 n ，那么，大于 n 的数字，就肯定不是未出现的最小正整数。

数据预处理

大于 n 的数字、负数、0，这些数字实际上都不应该被考虑，需要去掉，又要保证时间复杂度为 \(O(N)\) ，因此不能将这些元素弹出。我们可以将这些数用 1 替换。为了确保缺失的第一个正数不是 1，先要在这步操作前确定 1 是否存在（特判）。

1.png

如何实现就地算法

现在我们有一个只包含正数的数组，范围为 1 到 n，现在的问题是在 \(O(N)\) 的时间和常数空间内找出首次缺失的正数。如果可以使用哈希表，且哈希表的映射是 正数 -> 是否存在 的话，这其实很简单。"脏工作环境" 的解决方法是将一个字符串 hash_str 分配 n 个 0，并且用类似于哈希表的方法，如果在数组中出现数字 i 则将字符串中 hash_str[i] 修改为 1 。

1
2
3
4
5
O(N) space complexity solution with hash-map
[3,4,1,1,1,5,1,1,2,1] --> {1:6, 2:1, 3:1, 1:4, 5:1 6:missing]  # 统计出现次数

O(1) space complexity solution with hash-map
[3,4,1,1,1,5,1,1,2,1] --> "11111100000"  # 出现过就是0

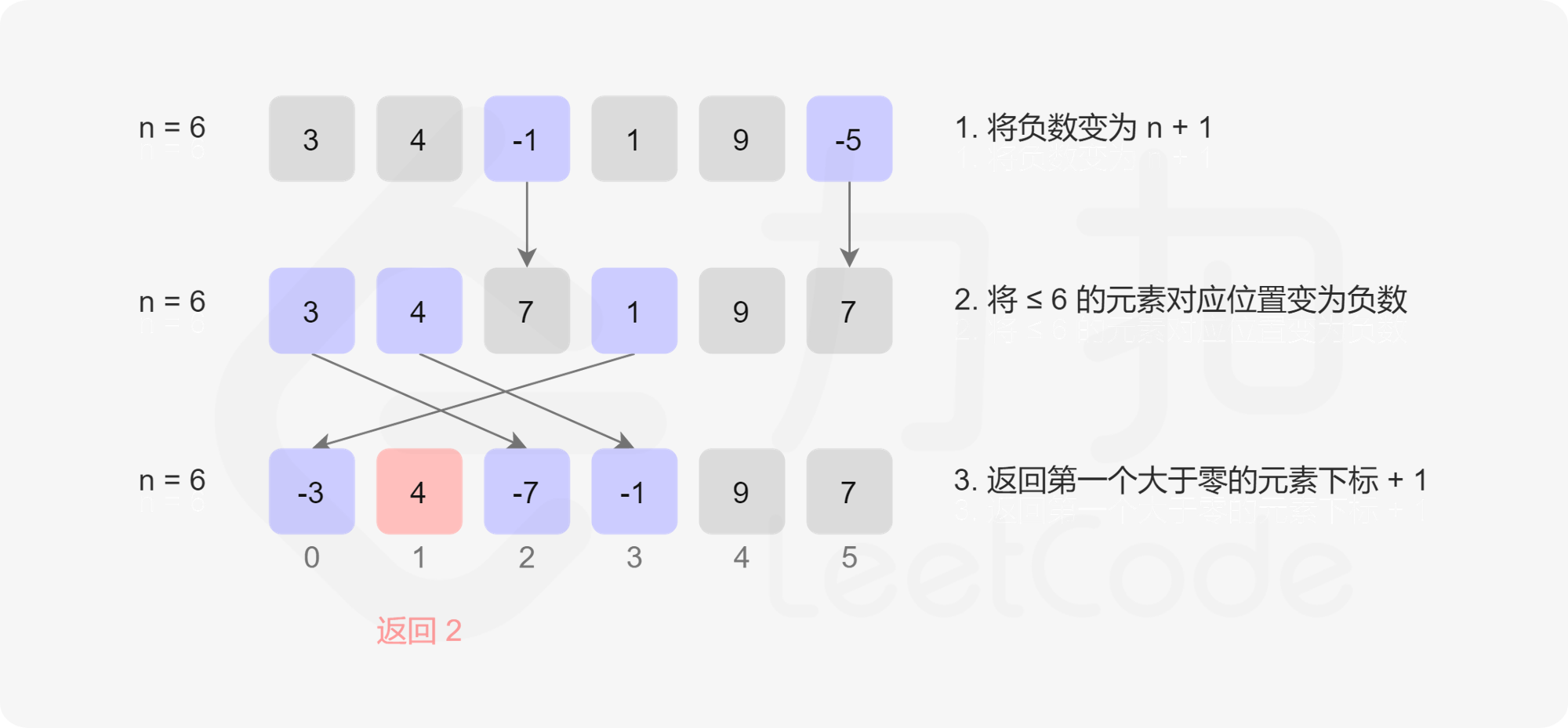
我们不使用这种方法，但是借鉴这种 使用索引作为哈希键值 的想法。最终的想法是 使用索引作为哈希键 以及 元素的符号作为哈希值 来实现是否存在的检测。为了完成此操作，我们遍历一遍数组（该操作在数据预处理使得数组中只有正数的操作后），检查每个元素值 elem 以及将nums[elem] 元素的符号变为负号来表示数字 elem 出现在 nums 中。注意，当数字出现多次时需要保证符号只会变化 1 次，负负得正，出现两次，反而又变回去正号了。

简而言之：以下标索引为哈希键（key），以正负号为哈希值（value）表示是否出现。 数组内心OS：我拿我自己当哈希表。

算法

  • 检查 1 是否存在于数组中。如果没有，则已经完成，1 即为答案。
  • 如果 nums = [1]，答案即为 2 。
  • 将负数，零，和大于 n 的数替换为 1 。
  • 遍历数组。当读到数字 a 时，替换第 a 个元素的符号。
  • 注意重复元素：只能改变一次符号。由于没有下标 n ，使用下标 0 的元素保存是否存在数字 n。
  • 再次遍历数组。返回第一个正数元素的下标。
  • 如果 nums[0] > 0，则返回 n 。
  • 如果之前的步骤中没有发现 nums 中有正数元素，则返回 n + 1。

代码步骤

1、特判1：1不在nums中的情况，未曾出现的最小正整数就是1。特判2：上面的特判已经检查了nums里面没有1的情况，那么能执行到这里，nums肯定就是包含了1，如果与此同时，len(nums) = 1，则nums就是[1]，相应的未曾出现的最小正整数就是2。
2、预处理，用 1 替换负数，0，和大于 n 的数，在转换以后，nums 只会包含正数。
3、使用索引和数字符号作为检查器，例如，如果 nums[1] 是负数表示在数组中出现了数字 1，如果 nums[2] 是正数 表示数字 2 没有出现，注意重复元素只需操作一次，所以每次取反的时候，都使用 nums[a] = - abs(nums[a]) 。关键代码 for i in range(n): 。由于长度为n的数组，下标范围为[0, n-1]，也就是说没有nums[n]来表示n的出现情况，这时使用下标0的元素的正负来表示是否存在数字n。
4、for循环先判断前面1到n-1有没有第i个数字没出现，如果有，就返回i。
5、数字n在长度为n的数组里面，是最后一个，如果前面1到n-1都出现了（上面的for循环就是干这个事情），就会执行到这里，通过判断nums[0]的正负，来检查第n个数字是否出现，nums[0]为正数，数字n没出现，否则就是出现了。
6、如果第n个数字也出现了（nums[0] < 0），例如n=8，nums=[1, 2, 3, 4, 5, 6, 7, 8]，则返回n + 1，也就是9，为最新未出现正整数。

LeetCode题解

Code

Python版本

方法一的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class Solution:
    def firstMissingPositive(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        n = len(nums)
        
        # 特判1：1不在nums中的情况，未曾出现的最小正整数就是1。
        if 1 not in nums:
            return 1
        
        # 特判2：上面的特判已经检查了nums里面没有1的情况，那么能执行到这里，nums肯定就是包含了1，且len(nums) = 1，则nums就是[1]，相应的未曾出现的最小正整数就是2。
        if n == 1:
            return 2
        
        # 预处理，用 1 替换负数，0，和大于 n 的数，在转换以后，nums 只会包含正数。
        for i in range(n):
            if nums[i] <= 0 or nums[i] > n:
                nums[i] = 1
        
        # 使用索引和数字符号作为检查器，例如，如果 nums[1] 是负数表示在数组中出现了数字 1，如果 nums[2] 是正数 表示数字 2 没有出现
        for i in range(n): 
            a = abs(nums[i])  # 如果发现了一个数字 a，改变第 a 个元素的符号为负号。
            # 注意重复元素只需操作一次
            if a == n:  # 由于长度为n的数组，下标范围为[0, n-1]，也就是说没有nums[n]来表示n的出现情况，这时使用下标0的元素的正负来表示是否存在数字n。
                nums[0] = - abs(nums[0])  # 在取反之前，abs取一下绝对值，保证了即使遇到了重复数字，最终效果也是只取反了一次。
            else:
                nums[a] = - abs(nums[a])
            
        # 先判断前面1到n-1有没有第i个数字没出现，如果有，就返回i。
        for i in range(1, n):
            if nums[i] > 0:
                return i
        
        # 数字n在长度为n的数组里面，是最后一个，如果前面1到n-1都出现了（上面的for循环就是干这个事情），就会执行到这里，通过判断nums[0]的正负，来检查第n个数字是否出现，nums[0]为正数，数字n没出现，否则就是出现了。
        if nums[0] > 0:
            return n
        
        # 如果第n个数字也出现了（nums[0] < 0），例如n=8，nums=[1, 2, 3, 4, 5, 6, 7, 8]，则返回n + 1，也就是9。
        return n + 1


print("leet code accept!!!")
Input = [[1,2,0], [3,4,-1,1], [7,8,9,11,12]]
Answer = [3, 2, 1]

if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)):
        print("-"*50)
        reslut = solution.firstMissingPositive(Input[i])
        print(reslut==Answer[i])

时间复杂度： \(O(N)\) 由于所有的操作一共只会遍历长度为 N 的数组 4 次。
空间复杂度： \(O(1)\) 由于只使用了常数的空间。
执行用时 :36 ms, 在所有 Python3 提交中击败了83.38%的用户
内存消耗 :13.4 MB, 在所有 Python3 提交中击败了32.50%的用户

Java版本

方法一的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        // 将小于0的负数变成n+1
        for (int i = 0; i < n; i++) {
            if (nums[i] <= 0) {
                nums[i] = n + 1;
            }
        }
        // 将小于等于n的元素对应位置变为负数，之前的负数位置由于变成了n+1，在这里就不会参与处理了。
        for (int i = 0; i < n; i++) {
            int num = Math.abs(nums[i]);
            if (num <= n) {
                nums[num - 1] = -Math.abs(nums[num - 1]);
            }
        }
        // 返回第一个大于零的元素的下标
        for (int i = 0; i < n; ++i) {
            if (nums[i] > 0) {
                return i + 1;
            }
        }
        return n + 1;
    }
}
41_fig1