LeetCode 39. 组合总和（中）

先排序后回溯，加法回溯逼近target，减法回溯逼近0。

题目

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的数字可以无限制重复被选取。 说明： 所有数字（包括 target）都是正整数。 解集不能包含重复的组合。

示例

示例 1:

1
2
3
4
5
6
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
  [7],
  [2,2,3]
]

示例 2: 

1
2
3
4
5
6
7
输入: candidates = [2,3,5], target = 8,
所求解集为:
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

考察知识点

数组、回溯算法

1
2
3
4
5
6
7
8
9
10
result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)  # 路径就是要添加的结果
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

核心思想

方法一、减法回溯

基本思路：

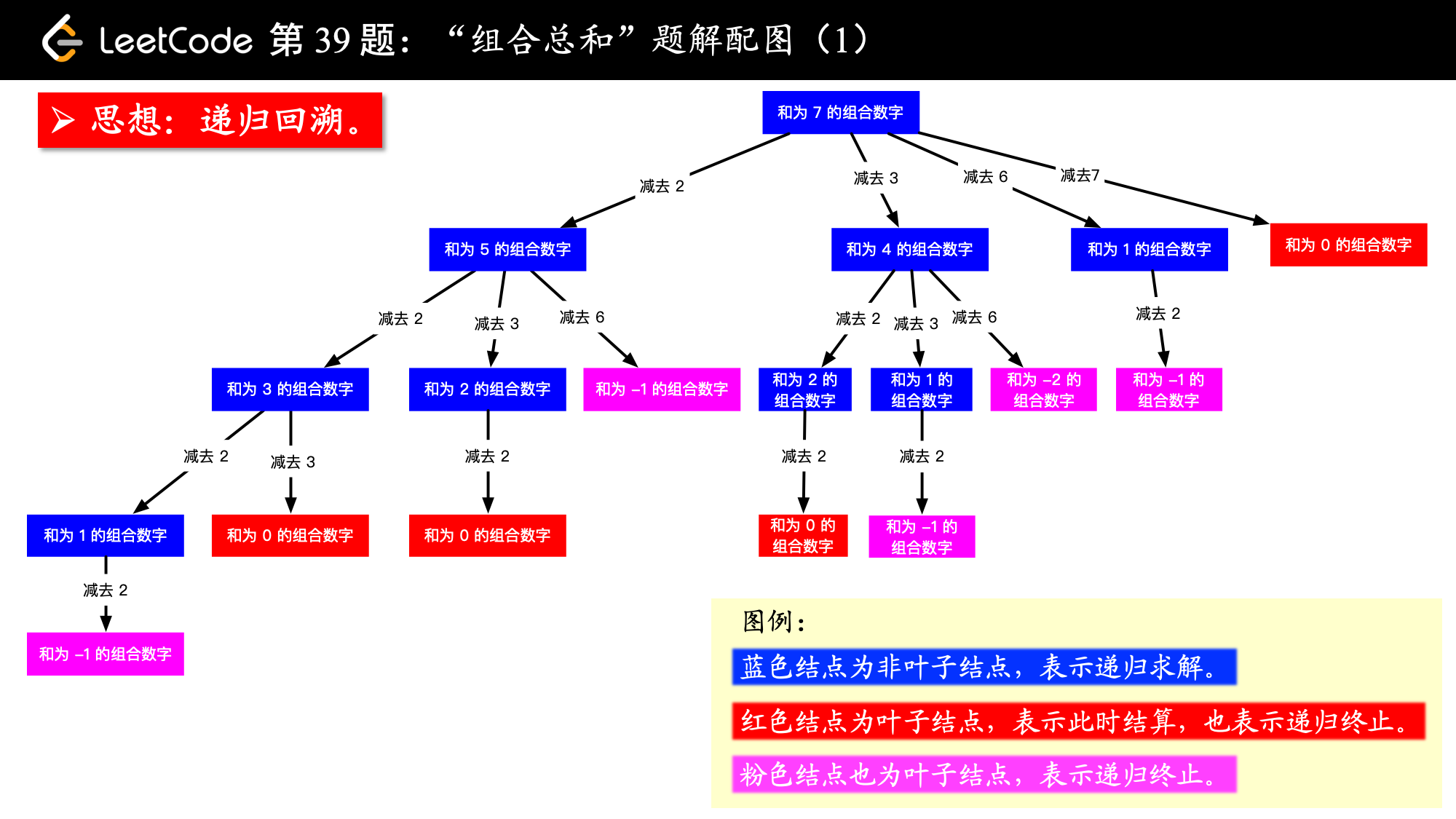
根据示例 1：输入: candidates = [2,3,6,7]，target = 7，输出：[[2, 2, 3], [7]]，候选数组里有 2 ，如果找到了 7 - 2 = 5 的所有组合，再在之前加上 2 ，就是 7 的所有组合； 同理考虑 3，如果找到了 7 - 3 = 4 的所有组合，再在之前加上 3 ，就是 7 的所有组合，依次这样找下去； 上面的思路就可以画成下面的树形图。

1.png

蓝色结点表示：尝试找到组合之和为该数的所有组合，怎么找呢？逐个减掉候选数组中的元素即可； 以 target = 7 为根结点，每一个分支做减法； 减到 0 或者负数的时候，到了叶子结点； 减到 0 的时候结算，这里 “结算” 的意思是添加到结果集； 从根结点到叶子结点（必须为 0）的路径，就是题目要我们找的一个组合。

改进方案：

2.png

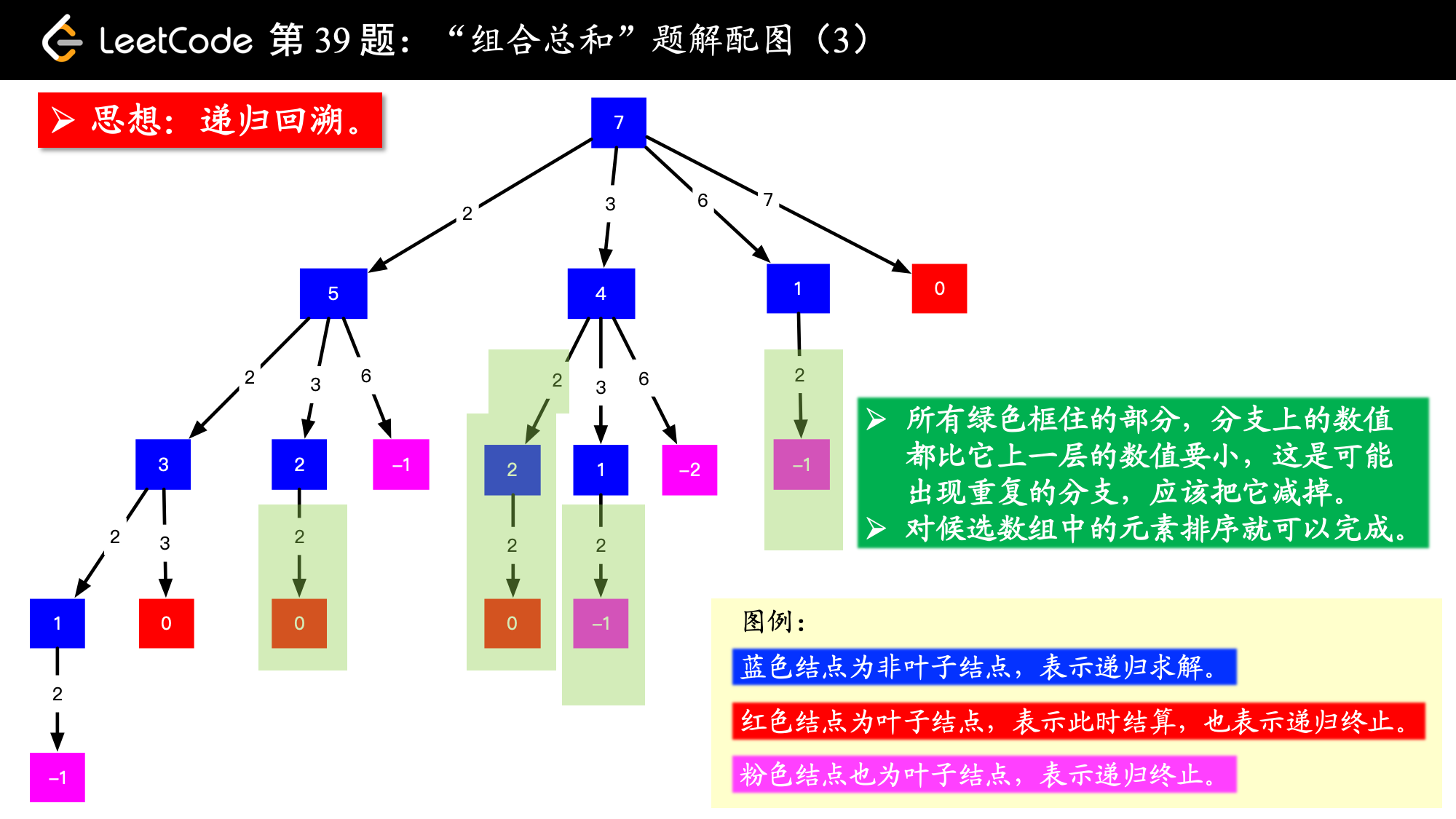
画出图以后，我看了一下，我这张图画出的结果有 4个 0，对应的路径是 [[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]]，而示例中的解集只有 [[7], [2, 2, 3]]，很显然，重复的原因是在较深层的结点值考虑了之前考虑过的元素，因此我们需要特别设置“下一轮搜索的起点”。

去重复

  • 在搜索的时候，需要设置搜索起点的下标 begin ，由于一个数可以使用多次，下一层的结点从这个搜索起点开始搜索；
  • 在搜索起点 begin 之前的数因为以前的分支搜索过了，所以一定会产生重复，一定要去掉。

剪枝提速

  • 如果一个数位搜索起点都不能搜索到结果，那么比它还大的数肯定搜索不到结果，基于这个想法，我们可以对输入数组进行排序，以减少搜索的分支。
  • 排序是为了提高搜索速度，非必要。
  • 搜索问题一般复杂度较高，能剪枝就尽量需要剪枝。把候选数组排个序，遇到一个较大的数，如果以这个数为起点都搜索不到结果，后面的数就更搜索不到结果了。
  • 剪枝：执行用时 :48 ms, 在所有 Python3 提交中击败了96.58%的用户。内存消耗 :13.5 MB, 在所有 Python3 提交中击败了30.29%的用户。
  • 不剪枝：执行用时 :88 ms, 在所有 Python3 提交中击败了46.61%的用户。内存消耗 :13.5 MB, 在所有 Python3 提交中击败了30.29%的用户。

代码步骤

1、获取condidate长度，对[]做特判。先对输入的candidates进行排序，为后面的剪枝做准备。剪枝是为了提速，在本题非必需。声明path变量在遍历的过程中记录路径，它是一个栈。以及res变量，保存path。调用回溯函数，注意要传入 size ，在 __dfs 中，size会变化， 这里传进去一个固定的。
2、定义__dfs回溯函数
2.1、先写递归终止的情况，由于是减法回溯，所以最终停止的条件是target被减成0。Python 中可变对象是引用传递，因此需要将当前 path 里的值拷贝出来 或者 使用 path.copy()。
2.2、然后写入选择列表，首先计算残差。然后进行“剪枝”操作，之前已经把候选数组排序了，遇到一个较大的数，如果以这个数为起点都搜索不到结果，后面的数就更搜索不到结果了，不必递归到下一层，并且后面的分支也不必执行，直接break。
2.3、将当前candidates[index]添加到path中。
2.4、调用__dfs，递归寻找，需要特别设置“下一轮搜索的起点”，以防止重复，因为下一层不能比上一层还小，否则就会和前面的重复，起始索引还从 index 开始，不需要从第一个开始。
2.5、当前回溯结束之后，执行撤销选择（弹栈）

大佬题解

方法二、加法回溯

和方法一的思路一致，先排序，后回溯。不过把减法改成了加法。

Python版本

方法一的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
from typing import List

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        size = len(candidates)  # 获取condidate长度
        if size == 0:  # 对[]做特判
            return []

        # 先对输入的candidates进行排序，为后面的剪枝做准备。剪枝是为了提速，在本题非必需。
        candidates.sort()
        # 声明path变量在遍历的过程中记录路径，它是一个栈。以及res变量，保存path。
        path = []
        res = []
        # 调用回溯函数，注意要传入 size ，在 __dfs 中，size会变化， 这里传进去一个固定的。
        self.__dfs(candidates, 0, size, path, res, target)
        return res

    # 定义__dfs回溯函数
    def __dfs(self, candidates, begin, size, path, res, target):
        # 先写递归终止的情况，由于是减法回溯，所以最终停止的条件是target被减成0。
        if target == 0:  
            res.append(path[:])  # Python 中可变对象是引用传递，因此需要将当前 path 里的值拷贝出来 或者 使用 path.copy()
            return  # 保留 

        # 然后写入选择列表
        for index in range(begin, size):
            residue = target - candidates[index]  # 计算残差
            if residue < 0:  break  # “剪枝”操作，之前已经把候选数组排序了，遇到一个较大的数，如果以这个数为起点都搜索不到结果，后面的数就更搜索不到结果了，不必递归到下一层，并且后面的分支也不必执行，直接break。如果不剪枝，也就是前面没有对candidate排序，这里就改成continue。
            self.__dfs(candidates, index, size, path + [candidates[index]], res, residue)  # 调用__dfs，递归寻找，需要特别设置“下一轮搜索的起点”，以防止重复，因为下一层不能比上一层还小，否则就会和前面的重复，起始索引还从 index 开始，不需要从第一个开始。


print("leet code accept!!!")
Input = [[2,3,6,7], [2,3,5]]
Input1 = [7, 8]
Answer = [
    [
        [7],
        [2,2,3]
    ], 
    [
        [2,2,2,2],
        [2,3,3],
        [3,5]
    ]
]

if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)):
        print("-"*50)
        reslut = solution.combinationSum(Input[i], Input1[i])
        print(reslut)
        print(Answer[i])

另一种减法回溯的写法，感觉要简洁一点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution(object):
    def combinationSum(self, candidates, target):
        """
        :type candidates: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        if not candidates:
            return []
        if min(candidates) > target:
            return []
        candidates.sort()
        res = []

        def helper(candidates, target, temp_list):
            if target == 0:
                res.append(temp_list)
            if target < 0:
                return
            for i in range(len(candidates)):
                if candidates[i] > target:
                    break
                helper(candidates[i:], target - candidates[i], temp_list + [candidates[i]])
        helper(candidates,target,[])
        return res

方法二的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from typing import List
class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        def backtrack(candidates, begin, path, res, length):
            if sum(path) == target:
                res.append(path[:])
                return
            for index in range(begin, length):
                # recial = target - candidates[index]
                if (sum(path) + candidates[index]) > target:
                    break
                path.append(candidates[index])
                backtrack(candidates, index, path, res, length)
                path.pop()

        length = len(candidates)
        if length == 0:
            return []
        
        candidates.sort()
        path = []
        res = []
        backtrack(candidates, 0, path, res, length)
        return res

一个三行Python版本

1
2
3
4
5
6
7
8
class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        if target < 0 or len(candidates) <= 0:
            return []
        if target == 0:
            return [[]]
        return self.combinationSum(candidates[1:], target) + \
                [[candidates[0]] + cp for cp in self.combinationSum(candidates, target - candidates[0])]

有效语法糖

Python可变对象和不可变对象

“Python 中可变对象是引用传递，因此需要将当前 path 里的值拷贝出来“，这句话的意思。首先必须理解的是，python中一切的传递都是引用（地址），无论是赋值还是函数调用，不存在值传递。

可变对象和不可变对象 python变量保存的是对象的引用，这个引用指向堆内存里的对象，在堆中分配的对象分为两类，一类是可变对象，一类是不可变对象。不可变对象的内容不可改变，保证了数据的不可修改（安全，防止出错），同时可以使得在多线程读取的时候不需要加锁。

不可变对象（变量指向的内存的中的值不能够被改变） 当更改该对象时，由于所指向的内存中的值不可改变，所以会把原来的值复制到新的空间，然后变量指向这个新的地址。python中数值类型（int和float），字符串str，元组tuple都是不可变对象。 下面以int类型为例简单介绍。

1
2
3
4
a = 1
print id(a)    # 40133000L，整数1放在了地址为40133000L的内存中，a变量指向这个地址。
a += 1 
print id(a)    # 40132976L，整数int不可改变，开辟新空间存放加1后的int，a指向这个新空间。

可变对象（变量指向的内存的中的值能够被改变） 当更改该对象时，所指向的内存中的值直接改变，没有发生复制行为。python中列表list，字典dict，集合set都是可变对象。下面以list类型为例简单介绍。

1
2
3
4
5
6
7
8
a = [1,2,3]
print id(a)    # 44186120L。

a += [4,5]     # 相当于调用了a.extend([4])
print id(a)    # 44186120L，列表list可改变，直接改变指向的内存中的值，没开辟新空间。

a = a + [7,8]  # 直接+和+=并不等价，使用+来操作list时，得到的是新的list，不指向原空间。
print id(a)    # 44210632L

引用传递后的改变

1
2
3
4
5
6
7
a = [1,2,3]
b = a
b[0] = 2     # 由于list是可变对象，改变b时候会导致a的改变，a和b都是[2,2,3]

s = 'abc'
s2 = s
s2 += 'd'   # 由于str是不可变对象，s2是新建的对象，s2的修改不会影响s。s为'abc'，s2为'abcd'。

list注意点

1
2
3
4
5
6
7
8
9
10
11
12
13
a = [1,2,3]
b = a
a is b             # True，因为按引用传递，a和b存的地址（引用）是一样的，改变b相当于改变a。

b = a[:]
a is b            # False，想使用list的值却不想修改原list时可以使用[:]拷贝一份到新空间。

a =[ [0]*2 ]* 2   # 以这种方式创建一个二维list，此时a为[[0,0],[0,0]]。
a[0] == a[1]      # True，这种创建方法的机制是复制list，所以2个list其实是同一个list。

a[0][0] = 1       # 改变第一个list时第二个list也改变，此时a为[[1,0],[1,0]]。
a[0] += [1]       # 改变第一个list时第二个list也改变，此时a为[[1,0,1],[1,0,1]]。
a[0] = [1,2]      # a[0]指向创建的新list[1,2]。此时a[1]不变，a为[[1,2],[1,0,1]]。