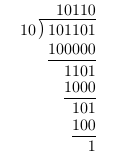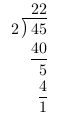LeetCode 29. 两数相除（中）

利用二分查找、位移运算可以实现两数相除。

题目

给定两个整数，被除数 dividend 和除数 divisor。将两数相除，要求不使用乘法、除法和 mod 运算符。返回被除数 dividend 除以除数 divisor 得到的商。

说明:
被除数和除数均为 32 位有符号整数。
除数不为 0。
假设我们的环境只能存储 32 位有符号整数，其数值范围是 [−231, 231 − 1]。本题中，如果除法结果溢出，则返回 231 − 1。

示例

示例 1: 

1
2
输入: dividend = 10, divisor = 3
输出: 3
示例 2: 
1
2
输入: dividend = 7, divisor = -3
输出: -2

考察知识点

数学、二分查找、位移运算

核心思想

方法一、位移运算

将10进制除法转换成2进制位移运算

10进制除法 2进制位移
b0b567805574f94e215153555d7bed5c3de04f3555bbae0e9c767afaf421d13d-2019-07-01 19-26-02屏幕截图.png Snipaste_2020-02-23_14-35-13.png

代码概述：

1、 确定最终的符号位。^是异或运算，当两者不同是返回1（负数），相同时返回0（正数）。
2、取10进制被除数和除数的绝对值。
3、把除数不断左移，直到它大于被除数，才可以用于后续移位计算。
4、申明变量result保存计算结果。
5、while循环在count退无可退的时候结束，代表运算结束。
6、count退一位，用于除数。由于之前除数大于被除数，在运算之前，要先把除数减小一倍。确保被除数可以减去除数。
7、前面divisor会一直退位，直到除数小于被除数。
8、的移位运算是把二进制（第count+1位上的1）转换为十进制
9、被除数减去当前除数，剩余部分再进行运算。
10、结束while循环，如果sign为1，则添加负数符号位，否则不做处理。
11、return时做极限值判定。

参考题解

方法二、二分查找

参考题解

Python版本

方法一实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution:
    def divide(self, dividend: int, divisor: int) -> int:
        sign = (dividend > 0) ^ (divisor > 0)  # 确定最终的符号位。^是异或运算，当两者不同是返回1（负数），相同时返回0（正数）。
        dividend = abs(dividend)  # 取10进制被除数的绝对值
        divisor = abs(divisor)  # 取10进制除数的绝对值
        count = 0  # count记录左移位数
        # 把除数不断左移，直到它大于被除数，才可以用于后续移位计算。
        while dividend >= divisor:
            count += 1
            divisor <<= 1
        result = 0  # 到这里除数dividend就大于被除数divisor了
        while count > 0:  # while循环在count退无可退的时候结束，代表运算结束。
            count -= 1  # count退一位，用于除数。
            divisor >>= 1  # 由于之前除数大于被除数，在运算之前，要先把除数减小一倍。确保被除数可以减去除数
            if divisor <= dividend:  # 前面divisor会一直退位，直到除数小于被除数。
                result += 1 << count # 这里的移位运算是把二进制（第count+1位上的1）转换为十进制
                dividend -= divisor  # 被除数减去当前除数，剩余部分再进行运算。
        if sign: result *= -1  # 结束while循环，如果sign为1，则添加负数符号位，否则不做处理。
        return result if -(1<<31) <= result <= (1<<31)-1 else (1<<31)-1  # return时做极限值判定。



print("leet code accept!!!")
Input = [45, 10, 7]
Input1 = [2, 3, -3]
Answer = [22, 3, -2]

if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)):
        print("-"*50)
        result = solution.divide(Input[i], Input1[i])
        print(result==Answer[i])

时间复杂度：\(O(n)\)
空间复杂度：只需要sign和count两个额外变量，\(O(1)\)。

二分查找方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution:
    def divide(self, dividend, divisor):
        if (divisor==0):
            return -1
        if (dividend==0):
            return 0
        # 特判 (-2147483648, -1) 这个测试样例
        if dividend == -(1<<31) and divisor == -1:
            return (1<<31)-1
        
        sgin = (dividend < 0) ^ (divisor < 0)
        res, div_count = 0, 1  # res是结果 div_count是倍增倍数默认倍增一倍
        dividend_tmp = abs(dividend)
        divisor_tmp = abs(divisor)

        while dividend_tmp >= divisor_tmp:
            dividend_tmp -= divisor_tmp
            res += div_count  # 每减一次divisor_tmp，计算结果res就加上一个div_count
            
            if dividend_tmp < abs(divisor):
                break

			# divisor_tmp无法倍增时，就将其初始化为divisor绝对值，重新开始下一轮倍增
            if dividend_tmp - divisor_tmp < divisor_tmp:
                divisor_tmp = abs(divisor)
                div_count = 1
                continue

			# 不断倍增divisor_tmp直到和dividend_tmp一样大
            divisor_tmp += divisor_tmp
            div_count += div_count
        
        res = -res if sgin else res
    
        return res if -(1<<31) <= res <= ((1<<31)-1) else ((1<<31)-1)