LeetCode 60. 第k个排列（中）

用阶乘数系统解决排列问题

题目

给出集合 [1,2,3,…,n]，其所有元素共有 n! 种排列。按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

"123"
"132"
"213"
"231"
"312"
"321"

给定 n 和 k，返回第 k 个排列。

说明：给定 n 的范围是 [1, 9]。给定 k 的范围是 [1, n!]。

示例

示例 1:

1 2	`输入: n = 3, k = 3 输出: "213"`

示例 2:

1 2	`输入: n = 4, k = 9 输出: "2314"`

考察知识点

数学、回溯

这道题，虽然是一道中等难度的题，但是，其构造阶乘数系统和排列映射关系的方法，十分的巧妙。通过阶乘数系统，可以直接由 n=4, k=9 推出要返回的字符串是 '2314'，不需要回溯，时间复杂度大大降低。

核心思想

方法一、先回溯后排序

利用回溯法获得int类型数字排列，然后排序，接着输出第k-1个数字的字符串形式。

方法二、基于阶乘数系统

面试中主要有三种类型的排列问题： 1. 全排列 2. 下一个排列 3. 第 k 个排列（当前问题）

如果排列的顺序不重要，可以使用“交换”的思想回溯写出全排列。生成 $N!$ 个全排列需要时间 $\mathcal{O}(N \times N!)$。该算法可以解决第一类问题。

D.E. Knuth 算法按照字典顺序生成全排列，在 $\mathcal{O}(N)$ 时间内完成。该算法可以解决第二类问题。

但是这两个算法不能解决第三类问题：

良好的时间复杂度，即无回溯。
先前排列未知，即不能使用 D.E. Knuth 算法。

为了解决这两个问题，可以使用映射的思路，因为生成数字的排列更容易，降低算法的时间复杂度。

使用数字生成排列，然后映射到组合/子集/排列中。

这种方法也广泛用于密码破解算法。

为什么需要阶乘数系统

排列的每种情况都可以使用十进制或二进制数表示：

$k= \sum_{m=0}^{N-1} k_m 2^m, 0≤k_m≤1$

原理如下：

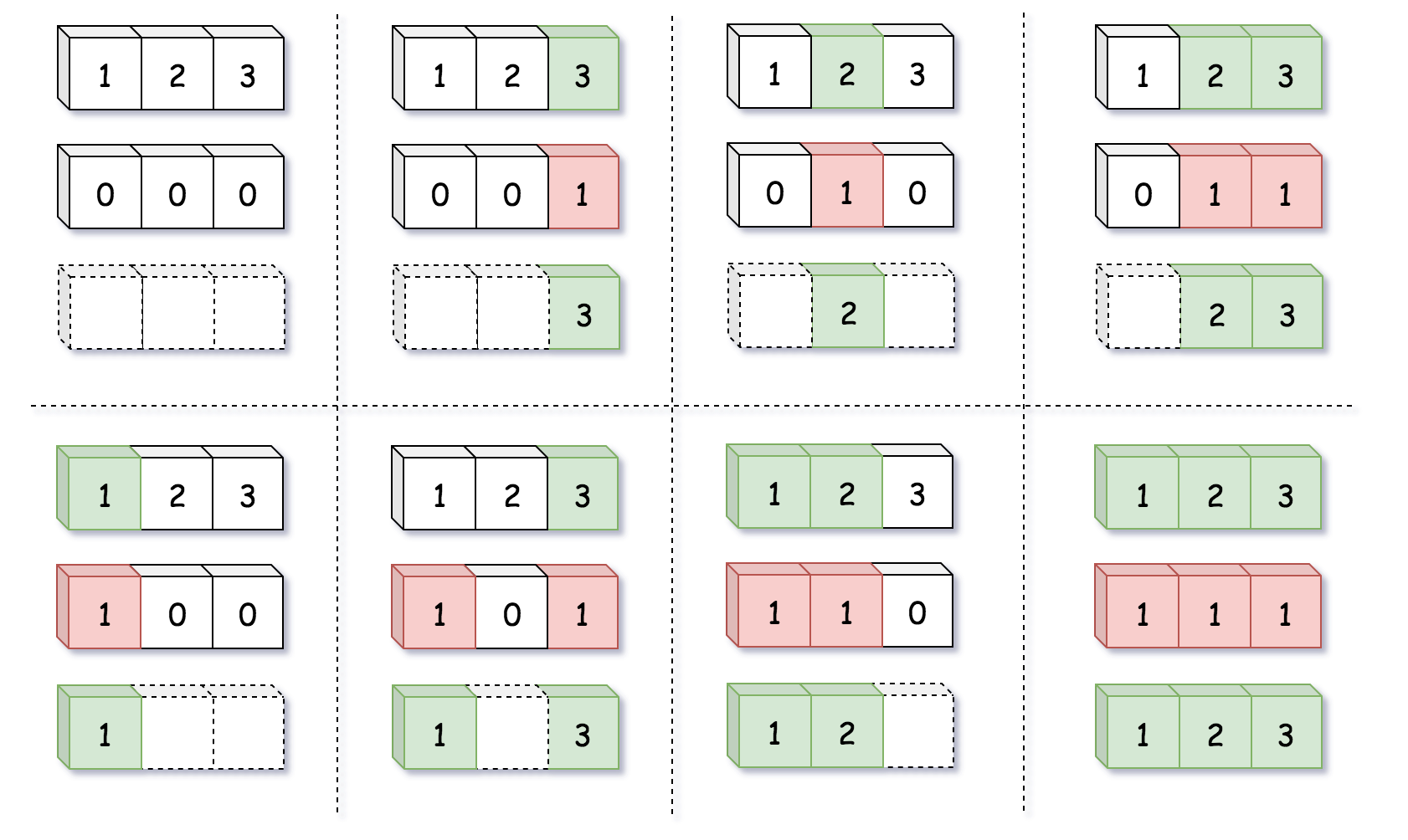
排列的问题在于排列的所有情况可能比数字表示的范围更大。$N$ 个元素的全排列数量为 $N!$，$N$ 位二进制包含 $2^N$ 个不同的数字。简单使用二进制数作为解空间不能包含排列的所有情况。

因此使用阶乘数系统，它具有非恒定基数：

$k = \sum\limits_{N−1}^{m=0} k_m m!,\ 0≤k_m≤m$

注意：权重（$k_m$）的大小不恒定，而是取决于基数（$m!$），当 $0 \le k_m \le m$ 时基数为 $m!$，例如 $k_0 = 0,\ 0 \le k_1 \le 1,\ 0 \le k_2 \le 2$ 等等。映射方式如下：

现在映射全部排列情况。从排列数 $k=0 = \sum\limits\_{m = 0}^{N - 1}{0 \times m!}$ 到排列数 $k=N! - 1 = \sum\limits_{m = 0}^{N - 1}{m \times m!}$

现在使用这些阶乘数构造全部的排列

如何从阶乘构造排列？已知N为输入nums长度，K为要输出的那个数字在排序之后所处的位置。

以N=3 ，即输入数组为 nums = [1, 2, 3]，k = 3 为例。排列的编号为从 0 到 N! - 1，而不是从 1 到 N!。因此 N = 3时，k = 2（数组排序是从0开始的，所以要在输入的k上减去1，从3变成2）。

首先构造 $k = 2$ 的阶乘数： $ k=2=1×2!+0×1!+0×0!=(1,0,0) $

阶乘中的系数表示输入数组中，除去已使用元素的索引。这符合每个元素只能在排列中出现一次的要求。

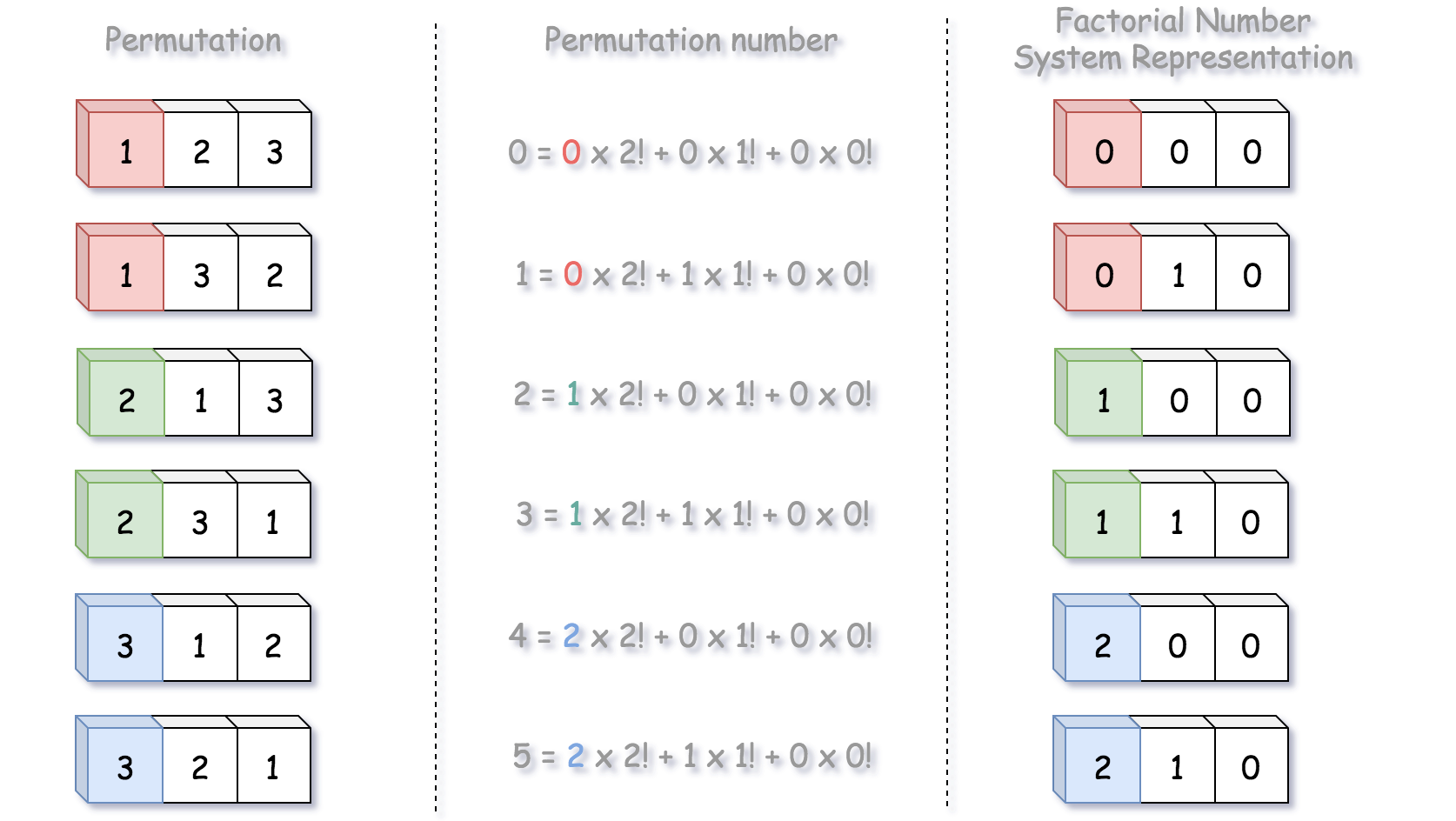
已知， $k = 2$ 的阶乘数为 $ k=2=1×2!+0×1!+0×0!=(1,0,0) $，可以发现第一个数字是 1，即排列中的第一个元素是 nums[1] = 2。由于每个元素只能使用一次，则从 nums 中删除该元素（也就是2），并将其加入到 output 变量中，nums中还剩1和3，此时 output = ['2']。

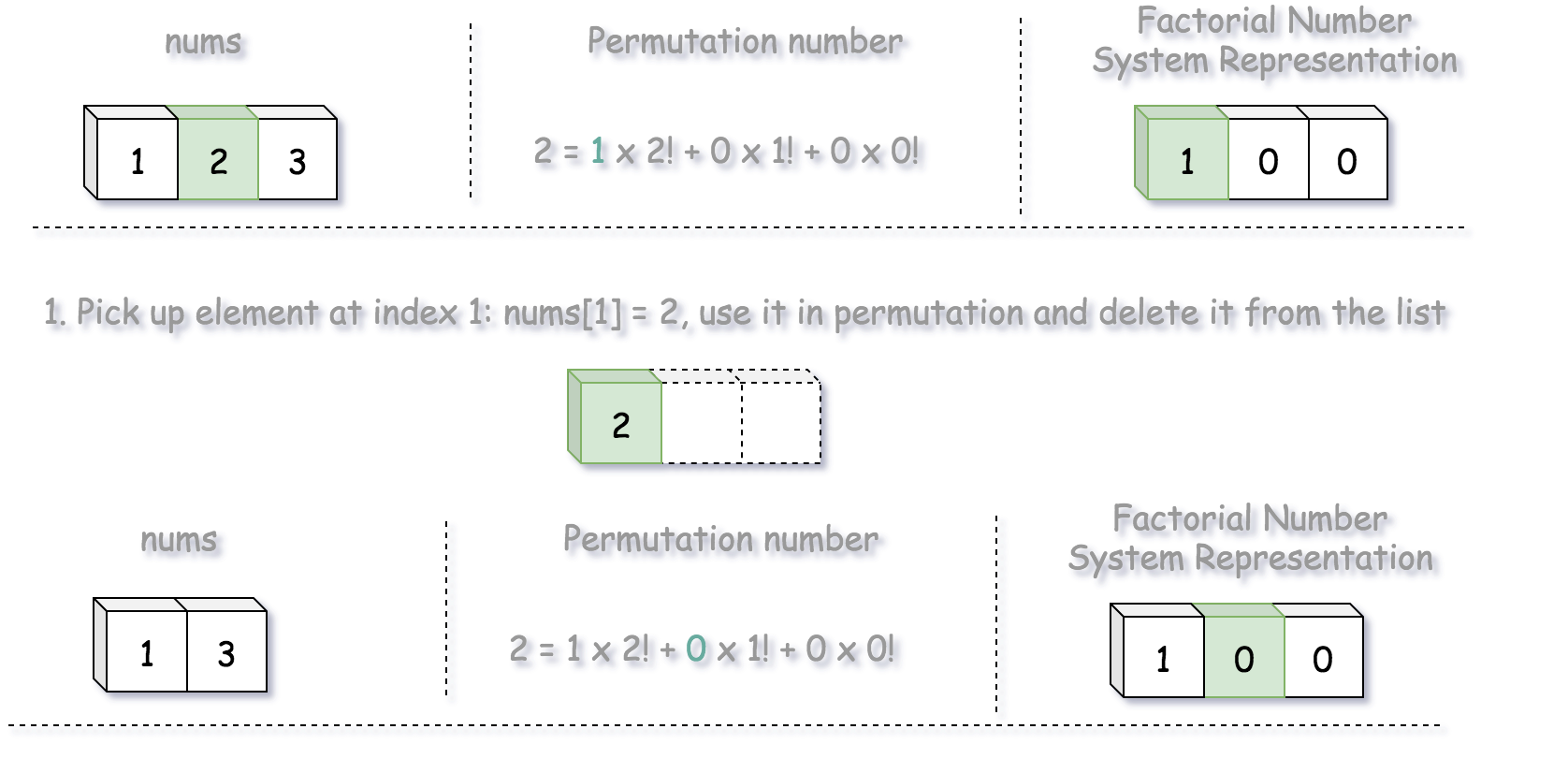
$ k=2=1×2!+0×1!+0×0!=(1,0,0) $ 阶乘中下一个系数为 0，即排列中 nums[0] = 1，然后从 nums 中删除该元素（也就是1），并将其加入到 output 变量中，nums中还剩3，output = ['2', '1']。

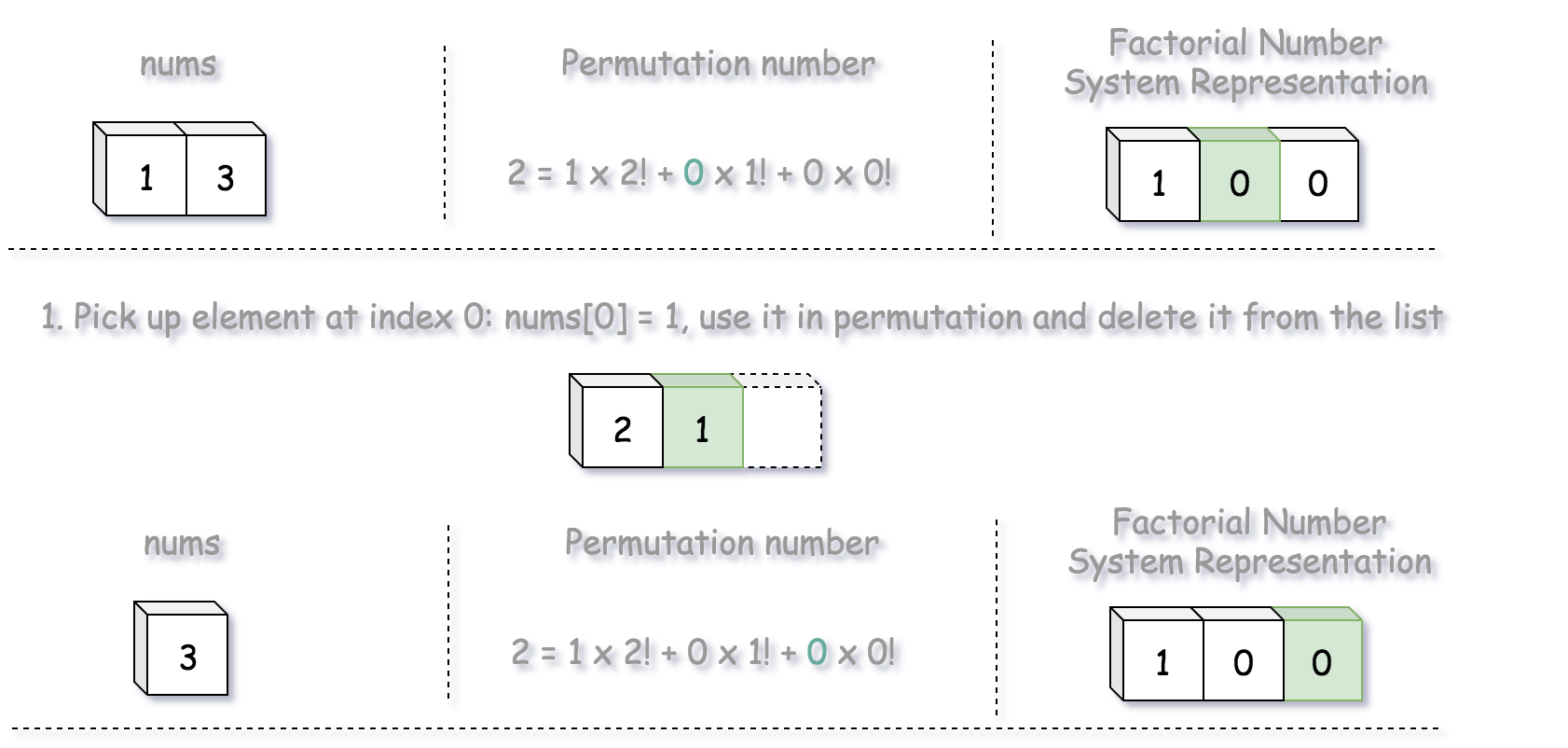
$ k=2=1×2!+0×1!+0×0!=(1,0,0) $ 阶乘中下一个系数也是 0，即排列中 nums[0] = 3，然后从 nums 中删除该元素（也就是3），并将其加入到 output 变量中，此时 output = ['2', '1', '3']。

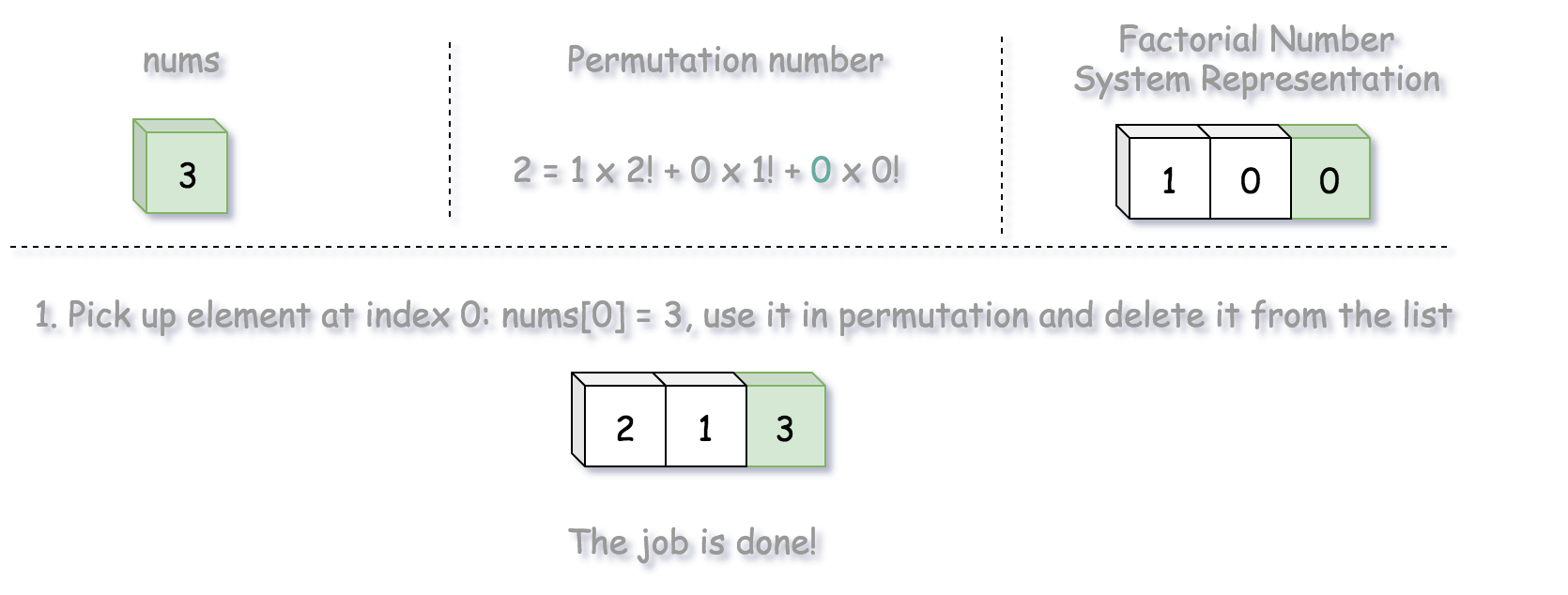
将以上关系简化为

输入N=3，K=3。实际上要求的是nums = [1, 2, 3]时第2位（从0开始）的排列组合。
k  排列组合  k的阶乘系数表示为   
2  213      1*2! + 0*1! + 0*0! = 2 = (1,0,0)  # (1, 0, 0)就是把系数提出来了。
从上面可以发现
由k的阶乘系数表示(1, 0, 0)去先获取nums对应位置数字,再删除再重新获取的结果就是'213',这样,我们就找到了nums = [1, 2, 3]，k=2和输出'213'之间的关系。

由k的阶乘系数表示(1, 0, 0)，nums = [1, 2, 3]。
1、先获取nums[1]（也就是2） ---> 2
2、再删除已经获取了的2，nums = [1, 3]。
3、再获取nums[0]（也就是1） ---> 1
4、然后删除已经获取了的1，nums = [3]。
5、最后获取nums[0]（也就是3） ---> 3
6、最后删除已经获取了的3，nums = []。
7、当nums为空时，我们依次获取的2、1、3组成的字符串'213'，就是最终答案。

算法

声明保存阶层数的变量 factorials，factorials[0] 就是 1，以及存储从 1 到 N 的数字的变量 nums，nums[0] 是 '1'。
开始循环生成 factorials 和 nums
- 计算从 0 到 (N - 1)! 的所有阶乘数，factorials.append(factorials[i - 1] * i)。
- 生成输入数组，存储从 1 到 N 的数字，nums.append(str(i + 1))。
k 减去 1（数组排序是从0开始的，所以要在输入的k上减去1），声明保存结果的变量 output。
开始循环计算 k 的阶乘表示，循环范围从 n - 1 到 0。
- 已知 $k = k_0 ! + k_1 ! + ... + k_m m! $ ，则计算当前阶乘 $m!$ 对应的阶乘系数 $k_m$。
- 更新 $k$。
- 将阶乘系数对应的数选中放入output中。
- 再从nums中删除这次被选中的数字
返回选中的排列字符串output的字符串形式。

LeetCode题解

Python版本

方法一的实现，这个方法在n大于8时就会超时。

class Solution:
    def getPermutation(self, n: int, k: int) -> str:
        if n == 1:
            return "1"

        nums = list(range(1, n+1))
        parmutations = self.generatePermute(nums)
        parmutations.sort()

        return str(parmutations[k-1])

    def generatePermute(self, nums):
        def backtrack(path=[], depth=0):
            if depth == length:
                tmp_d = int(''.join(path[:]))
                output.append(tmp_d)
                # output.append(int(''.join(path[:])))
                return

            for index in range(length):
                if not used[index]:
                    path.append(str(nums[index]))
                    used[index] = True
                    backtrack(path, depth+1)
                    path.pop()
                    used[index] = False

        output = []
        length = len(nums)
        used = [False] * length
        backtrack()
        return output

print("leet code accept!!!")
Input = [9, 3, 4]
Input1 = [273815, 3, 9]
Answer = ["783269514", "213", "2314"]


if __name__ == "__main__":
    solution = Solution()
    for i in range(len(Input)):
        print("-"*50)
        reslut = solution.getPermutation(Input[i], Input1[i])
        print(reslut == Answer[i])

时间复杂度 $O(N \times N!)$ 空间复杂度 $O(N×N!)$

方法二的实现

class Solution:
    def getPermutation(self, n: int, k: int) -> str:
        factorials, nums = [1], ['1']  # 声明保存阶层数的变量factorials，factorials[0]就是1，以及存储从 1 到 N 的数字的变量nums，nums[0]是'1'。
        
        for i in range(1, n):
            # 计算从 0 到 (N - 1)!的所有阶乘数。
            factorials.append(factorials[i - 1] * i)
            # 生成输入数组，存储从 1 到 N 的数字。
            nums.append(str(i + 1))

        k -= 1  # 数组排序是从0开始的，所以要在输入的k上减去1
        
        output = []  # 声明保存结果的output
        # 开始循环计算k的阶乘表示，循环范围从n - 1到0。
        for m in range(n - 1, -1, -1):
            # 计算 k 的阶乘表示，使用阶乘系数构造排列。
            # 已知 k = k_0 * 0! + k_1 * 1! + ... + k_m * m!
            k_m = k // factorials[m]  # 计算计算当前阶乘 m! 对应的阶乘系数 k_m。
            k -= k_m * factorials[m]  # 更新k

            output.append(nums[k_m])  # 将阶乘系数对应的数选中放入output中
            del nums[k_m]  # 再从nums中删除这次被选中的数字
        
        return ''.join(output)  # 返回选中的排列字符串output的字符串形式。

时间复杂度：$\mathcal{O}(N^2)$，从列表中删除元素，共执行操作次数：$N + (N - 1) + ... + 1 = N(N - 1)/2$ 空间复杂度：$\mathcal{O}(N)$。执行用时 :36 ms, 在所有 Python3 提交中击败了64.41%的用户内存消耗 :13.3 MB, 在所有 Python3 提交中击败了20.80%的用户

有效语法糖

1、如果外层声明的变量，内层要使用，可能会出现下面这种情况，output会报错未声明。

def generatePermute(self, nums):
    def backtrack(path=[], depth=0):
        if depth == length:
            # 第一种方式
            output.append(int(''.join(path[:])))  # 直接往output中添加元素就会报错output未声明，可能是由于要添加的内容太过复杂
            # 第二种方式
            tmp_d = int(''.join(path[:]))
            output.append(tmp_d)  # 这样，先获取后添加，就不会报错，以后如果在添加之前要进行复杂的处理，请先单独处理后保存在一个变量中，再添加。                
            return

        for index in range(length):
            if not used[index]:
                path.append(str(nums[index]))
                used[index] = True
                backtrack(path, depth+1)
                path.pop()
                used[index] = False

    output = []
    length = len(nums)
    used = [False] * length
    backtrack()
    return output

LeetCode

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

LeetCode 12. 整数转罗马数字（中）上一篇

LeetCode 10. 正则表达式匹配（难）& 面试题19. 正则表达式匹配（难）下一篇