循环遍历、两两合并、分治、暴力破解、注意对比,五种方法解决该问题。
题目
合并 k 个排序链表,返回合并后的排序链表。请分析和描述算法的复杂度。
示例
| 输入:
[
1->4->5,
1->3->4,
2->6
]
输出: 1->1->2->3->4->4->5->6
|
考察知识点
堆、链表、分治思想
核心思想
方法一、暴力破解
思路很简单:
- 遍历所有链表,将所有节点的值放到一个数组中。
- 将这个数组排序,然后遍历所有元素得到正确顺序的值。
- 用遍历得到的值,创建一个新的有序链表。
方法二、逐一比较
- 比较 \(\text{k}\) 个节点(每个链表的首节点),获得最小值的节点。
- 将选中的节点接在最终有序链表的后面。
方法三、用优先队列优化方法二
几乎与上述方法一样,除了将 比较环节 用 优先队列 进行了优化。你可以参考 这里 获取更多信息。
方法四、逐一两两合并链表
将合并 \(\text{k}\) 个链表的问题转化成合并 2 个链表 \(\text{k-1}\)次。
方法五、分治
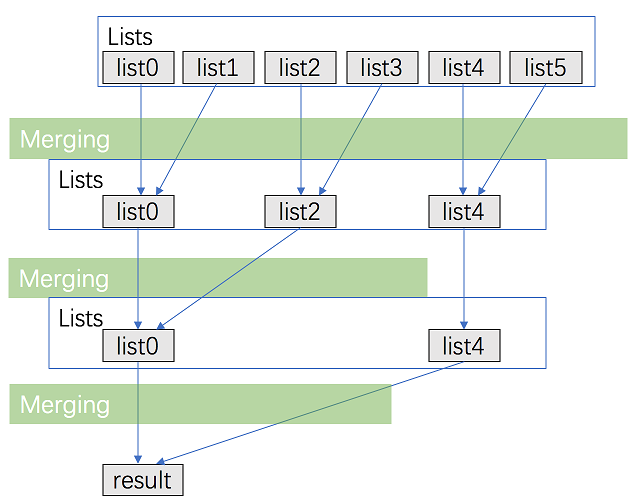
这个方法沿用了上面的解法,但是进行了较大的优化。我们不需要对大部分节点重复遍历多次。 将 \(\text{k}\) 个链表配对并将同一对中的链表合并。 第一轮合并以后, \(\text{k}\) 个链表被合并成了 \(\frac{k}{2}\)个链表,平均长度为 \(\frac{2N}{k}\),然后是 \(\frac{k}{4}\) 个链表,\(\frac{k}{8}\) 个链表等等。 重复这一过程,直到我们得到了最终的有序链表。 因此,我们在每一次配对合并的过程中都会遍历几乎全部 \(N\) 个节点,并重复这一过程 \(\log_2K\) 次。
LeetCode题解
Python版本
暴力破解版
暴力破解加希尔排序,实际上是效果最好的,比分治算法更快。 这可能和使用的是Python语言编程有关。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution:
def mergeKLists(self, lists: list) -> ListNode:
if not len(lists):
return None
sum_l = []
for l in lists:
while l:
sum_l.append(l.val)
l = l.next
if len(sum_l):
sum_l.sort()
root = ListNode(sum_l[0])
tmp = root
for i in range(1, len(sum_l)):
tmp.next = ListNode(sum_l[i])
tmp = tmp.next
return root
else:
return None
|
时间复杂度:\(O(N\log N)\) ,其中 N是节点的总数目。 遍历所有的值需花费 \(O(N)\) 的时间。 一个稳定的排序算法花费 \(O(N\log N)\) 的时间。 遍历同时创建新的有序链表花费 \(O(N)\) 的时间。
空间复杂度:\(O(N)\)。 排序花费 \(O(N)\) 空间(这取决于你选择的算法)。 创建一个新的链表花费 \(O(N)\) 的空间。
执行用时 :76 ms, 在所有 Python3 提交中击败了98.94%的用户 内存消耗 :17.1 MB, 在所有 Python3 提交中击败了34.46%的用户
方法二、逐一比较法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution:
def mergeKLists(self, lists: list) -> ListNode:
prehead = ListNode(-1)
prev = prehead
is_finish = False
while not is_finish:
min_flag = 0
min_val = 1<<31
is_finish = True
for _index, l in enumerate(lists):
if l:
is_finish = False
if l and l.val < min_val:
min_val = l.val
min_flag = _index
if not is_finish:
prev.next = ListNode(min_val)
prev = prev.next
lists[min_flag] = lists[min_flag].next
return prehead.next
|
复杂度分析 时间复杂度: \(O(kN)\) ,其中 \(\text{k}\) 是链表的数目。 几乎最终有序链表中每个节点的时间开销都为 \(O(k)\) (\(\text{k-1}\) 次比较)。 总共有 N 个节点在最后的链表中。
空间复杂度: \(O(n)\) 。创建一个新的链表空间开销为 \(O(n)\) 。 \(O(1)\) 。重复利用原来的链表节点,每次选择节点时将它直接接在最后返回的链表后面,而不是创建一个新的节点
该算法,通过了一共131个测试样例中的130个,最后一个由10000个单节点链表组成的测试用例由于超时而没有通过。
方法三的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| from queue import PriorityQueue
class Solution(object):
def mergeKLists(self, lists):
"""
:type lists: List[ListNode]
:rtype: ListNode
"""
head = point = ListNode(0)
q = PriorityQueue()
for l in lists:
if l:
q.put((l.val, l))
while not q.empty():
val, node = q.get()
point.next = ListNode(val)
point = point.next
node = node.next
if node:
q.put((node.val, node))
return head.next
|
这个代码,跑不了,会报错,可能和API有关。
时间复杂度: \(O(N\log k)\) ,其中 \(\text{k}\) 是链表的数目。
弹出操作时,比较操作的代价会被优化到 \(O(\log k)\) 。同时,找到最小值节点的时间开销仅仅为 \(O(1)\)。 最后的链表中总共有 \(\text{N}\) 个节点。 空间复杂度:
\(O(n)\) 。创造一个新的链表需要 \(O(n)\) 的开销。 \(O(k)\) 。以上代码采用了重复利用原有节点,所以只要 \(O(1)\) 的空间。同时优先队列(通常用堆实现)需要 \(O(k)\) 的空间(远比大多数情况的 \(N\) 要小)。
方法四两两合并算法的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution():
def mergeKLists(self, lists):
def mergeTwoLists(l1, l2):
prehead = ListNode(-1)
prev = prehead
while l1 and l2:
if l1.val <= l2.val:
prev.next = l1
l1 = l1.next
else:
prev.next = l2
l2 = l2.next
prev = prev.next
prev.next = l1 if l1 is not None else l2
return prehead.next
if not len(lists):
return None
if len(lists) == 1:
return lists[0]
start_l = mergeTwoLists(lists[0], lists[1])
for i in range(2, len(lists)):
start_l = mergeTwoLists(start_l, lists[i])
return start_l
|
时间复杂度: \(O(kN)\),其中 \(\text{k}\) 是链表的数目。 我们可以在 \(O(n)\) 的时间内合并两个有序链表,其中 n 是两个链表的总长度。 把所有合并过程所需的时间加起来,我们可以得到: \(O(\sum_{i=1}^{k-1} (i*(\frac{N}{k}) + \frac{N}{k})) = O(kN)\) 。
空间复杂度:我们可以在 \(O(1)\) 空间内合并两个有序链表。
执行用时 :4640 ms, 在所有 Python3 提交中击败了9.50%的用户
内存消耗 :16.3 MB, 在所有 Python3 提交中击败了65.04%的用户
方法五、分治算法的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution(object):
def mergeKLists(self, lists):
"""
:type lists: List[ListNode]
:rtype: ListNode
"""
amount = len(lists)
interval = 1
while interval < amount:
for i in range(0, amount - interval, interval * 2):
lists[i] = self.merge2Lists(lists[i], lists[i + interval])
interval *= 2
return lists[0] if amount > 0 else lists
def merge2Lists(self, l1, l2):
head = point = ListNode(0)
while l1 and l2:
if l1.val <= l2.val:
point.next = l1
l1 = l1.next
else:
point.next = l2
l2 = l1
l1 = point.next.next
point = point.next
if not l1:
point.next = l2
else:
point.next = l1
return head.next
|
时间复杂度: \(O(N\log k)\) ,其中 \(\text{k}\) 是链表的数目。 我们可以在 \(O(n)\) 的时间内合并两个有序链表,其中 \(n\) 是两个链表中的总节点数。 将所有的合并进程加起来,我们可以得到:\(O\big(\sum_{i=1}^{log_2k}N \big)= O(N\log k)\)。
空间复杂度:\(O(1)\)我们可以用 \(O(1)\) 的空间实现两个有序链表的合并。
执行用时 :92 ms, 在所有 Python3 提交中击败了97.57%的用户
内存消耗 :16.3 MB, 在所有 Python3 提交中击败了65.20%的用户
有效语法糖
1、实现一个可迭代对象两两分治计算的写法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| amount = 20
interval = 1
while interval < amount:
print("-"*50)
for i in range(0, amount - interval, interval * 2):
print(i, i + interval)
interval *= 2
Output:
--------------------------------------------------
interval is 1
0 1
2 3
4 5
6 7
8 9
10 11
12 13
14 15
16 17
18 19
--------------------------------------------------
interval is 2
0 2
4 6
8 10
12 14
16 18
--------------------------------------------------
interval is 4
0 4
8 12
--------------------------------------------------
interval is 8
0 8
--------------------------------------------------
interval is 16
0 16
Output
--------------------------------------------------
interval is 1
0 1
2 3
4 5
6 7
8 9
10 11
12 13
14 15
16 17
18 19
--------------------------------------------------
interval is 2
0 2
4 6
8 10
12 14
16 18
--------------------------------------------------
interval is 4
0 4
8 12
16 20
--------------------------------------------------
interval is 8
0 8
--------------------------------------------------
interval is 16
0 16
|
