一道典型的回溯算法题目
题目
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
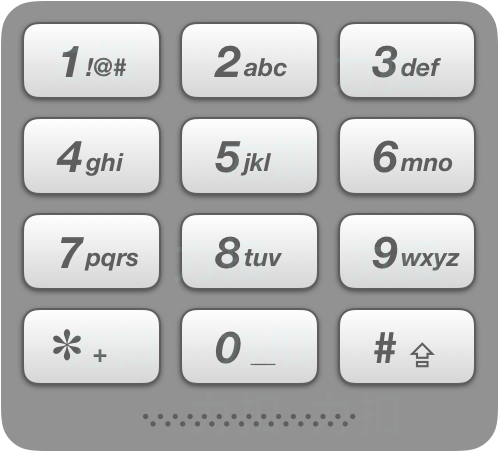
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
17_telephone_keypad.png
示例
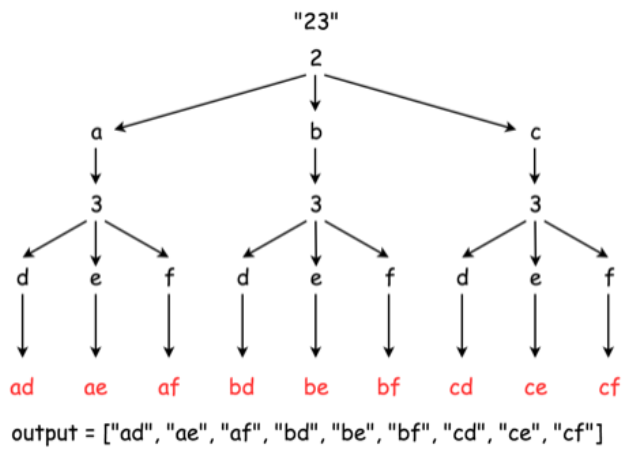
输入:"23" "ad" , "ae" , "af" , "bd" , "be" , "bf" , "cd" , "ce" , "cf" ].
考察知识点
字符串、回溯算法、深度遍历(DFS)、
核心思想
回溯是一种通过穷举所有可能情况来找到所有解的算法。如果一个候选解最后被发现并不是可行解 ,回溯算法会舍弃它,并在前面的一些步骤做出一些修改,并重新尝试找到可行解。
给出如下回溯函数 backtrack(combination, next_digits) ,它将一个目前已经产生的组合 combination 和接下来准备要输入的数字 next_digits 作为参数。 如果没有更多的数字需要被输入,那意味着当前的组合已经产生好了,可以直接添加。 如果还有数字需要被输入: 遍历下一个数字所对应的所有映射的字母。 将当前的字母添加到组合最后,也就是 combination = combination + letter 。 重复这个过程,输入剩下的数字: backtrack(combination + letter, next_digits[1:])
Snipaste_2020-02-20_00-14-09.png
LeetCode题解
Python版本
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution :def letterCombinations (self, digits ):'2' : ['a' , 'b' , 'c' ],'3' : ['d' , 'e' , 'f' ],'4' : ['g' , 'h' , 'i' ],'5' : ['j' , 'k' , 'l' ],'6' : ['m' , 'n' , 'o' ],'7' : ['p' , 'q' , 'r' , 's' ],'8' : ['t' , 'u' , 'v' ],'9' : ['w' , 'x' , 'y' , 'z' ]}def backtrack (combination, next_digits ):if not next_digits: else : for letter in phone[next_digits[0 ]]: 1 :]) if digits:"" , digits)return output"leet code accept!!!" )"23" ]"ad" , "ae" , "af" , "bd" , "be" , "bf" , "cd" , "ce" , "cf" ]]if __name__ == "__main__" :for i in range (len (Input)):"-" *50 )
时间复杂度: \(O(3^N \times 4^M)\) ,其中 N 是输入数字中对应 3 个字母的数目(比方说 2,3,4,5,6,8), M 是输入数字中对应 4 个字母的数目(比方说 7,9),N+M 是输入数字的总数。
空间复杂度:\(O(3^N \times 4^M)\) ,这是因为需要保存 \(3^N \times 4^M\) 个结果。