LeetCode 14. 最长公共前缀（易）

垂直扫描、水平扫描、二分查找、字典树多种方法都可以解决。

题目

编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀，返回空字符串 ""。 说明:所有输入只包含小写字母 a-z 。

示例

示例 1: 

1
2
输入: ["flower","flow","flight"]
输出: "fl"
示例 2: 
1
2
输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。

考察知识点

字符串、分治思想、二分查找

核心思想

方法类型一：扫描匹配法

  • 垂直扫描，思路简单，直接对比每个字符串前n个字符，如果相同就n+1，直到不相同为止。

  • 利用set、zip等Python3内建方法实现垂直扫描，利用set去重，利用zip将每个字符串前n个（n为最小字符串长度）个字符匹配，这个方法太依赖Python的内建函数，不推荐。

  • 水平扫描，思路清奇，简而言之就是设置第一个字符串为最大prefix，根据匹配结果一个字符一个字符的缩小，推荐。

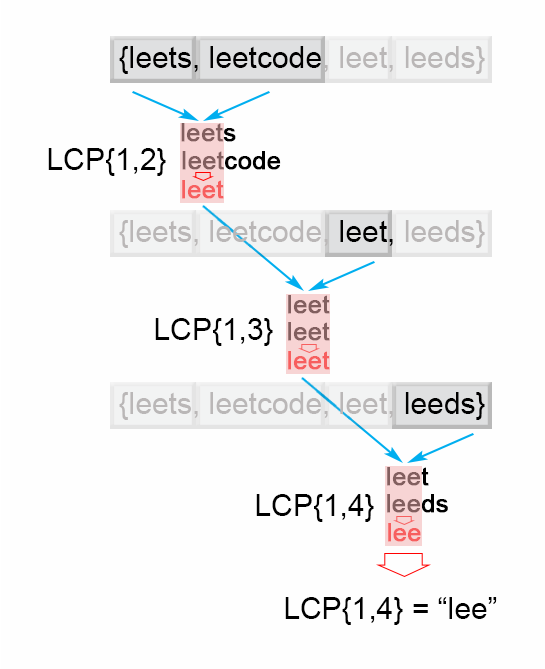
公共子串前缀的关键在于前缀必须是公共的，这就意味着，前面几个子串的公共前缀也必须满足后面的要求，所以可以依次遍历字符串\([S_1, S_2, S_3,...,S_n]\)，当遍历到第 \(i\) 个字符串的时候，找到最长公共前缀 \(LCP(S_1,,,S_i)\)。一旦\(LCP(S_1,,,S_i)\) 为空，意味着前\(i\)个字符串没有公共子串，后面就没必要找了，直接return ""。否则，在执行了 \(n\) 次遍历之后，算法就会返回最终答案 \(LCP(S_1,,,S_n)\)。

1.png

关键一句while strs[i].find(prefix) != 0: # 用这句话判断当前prefix是不是也是其他字符串的前缀

分治

\[ LCP(S_1,,,S_n)=LCP(LCP(S_1,,,S_k), LCP(S_{k+1},,,S_n)) \]

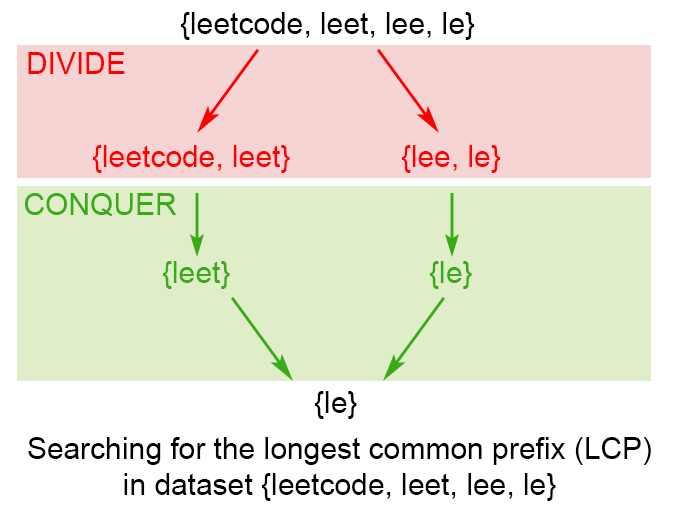
将原问题 \(LCP(S_1,,,S_n)\) 分成两个子问题 \(LCP(S_1,,,S_{mid})\) 与 \(LCP(S_{mid+1},,,S_n)\) ，其中 \(mid = \frac{i+j}{2}\) 。 我们用子问题的解 lcpLeft 与lcpRight 构造原问题的解 。 从头到尾挨个比较 lcpLeft与 lcpRight 中的字符，直到不能再匹配为止。 计算所得的 lcpLeft 与 lcpRight 最长公共前缀就是原问题的解。

8bb79902c99719a923d835b9265b2dea6f20fe7f067f313cddcf9dd2a8124c94-file_1555694229984.png

二分查找

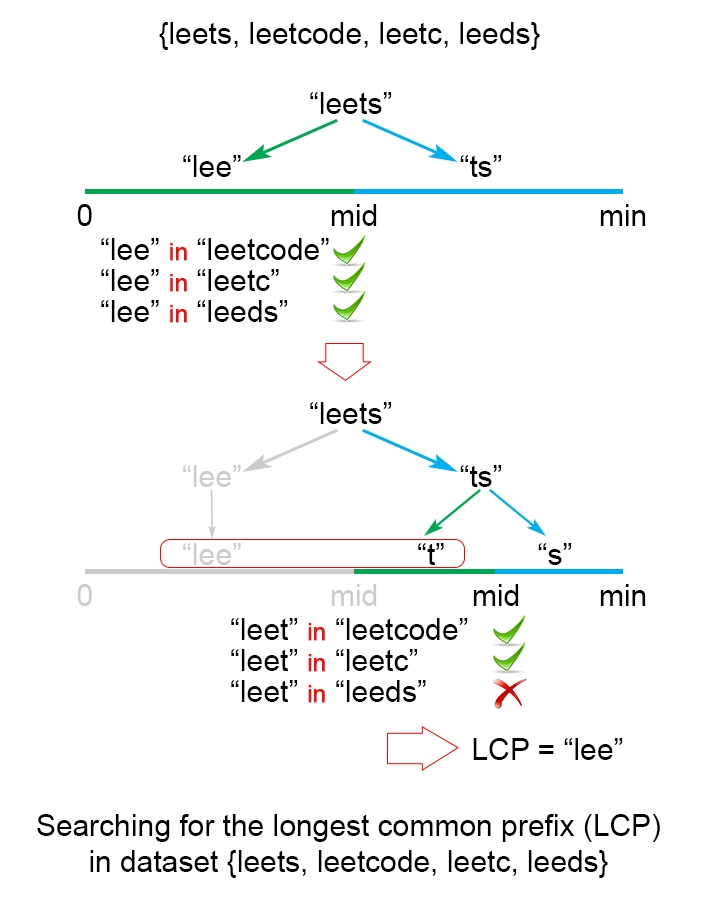
应用二分查找法找到所有字符串的公共前缀的最大长度 L。 算法的查找区间是 \((0 \ldots minLen)\)，其中 minLen 是输入数据中最短的字符串的长度，同时也是答案的最长可能长度。 每一次将查找区间一分为二，然后丢弃一定不包含最终答案的那一个。算法进行的过程中一共会出现两种可能情况：

\(S[1...mid]\) 不是所有串的公共前缀。 这表明对于所有的 \(j > i\ S[1..j]\) 也不是公共前缀，于是我们就可以丢弃后半个查找区间，缩小前区间的范围，继续往前寻找。

\(S[1...mid]\) 是所有串的公共前缀。 这表示对于所有的 \(i < j S[1..i]\) 都是可行的公共前缀，因为我们要找最长的公共前缀，所以我们可以把前半个查找区间丢弃，继续往后寻找。

这里判断是否所有串的公共前缀的方法是垂直扫描。

e41778494b56890e2bb7616504e2a0169bbdb409710262eaf5250c635adab9d6-file_1555694009677.png

基于字典树的方法

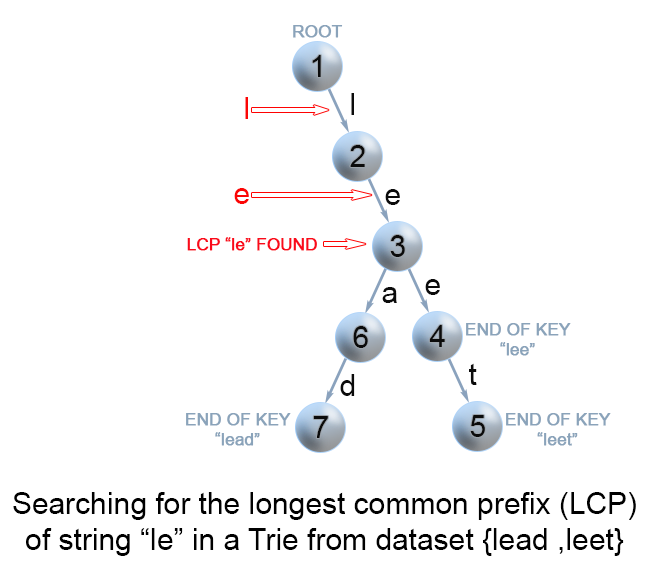
我们可以通过将所有的键值 S 存储到一颗字典树中来优化最长公共前缀查询操作。 如果你想学习更多关于字典树的内容，可以从 208. 实现 Trie (前缀树) 开始。在字典树中，从根向下的每一个节点都代表一些键值的公共前缀。 但是我们需要找到字符串q 和所有键值字符串的最长公共前缀。 这意味着我们需要从根找到一条最深的路径，满足以下条件：

  • 这是所查询的字符串 q 的一个前缀
  • 路径上的每一个节点都有且仅有一个孩子。 否则，找到的路径就不是所有字符串的公共前缀
  • 路径不包含被标记成某一个键值字符串结尾的节点。 因为最长公共前缀不可能比某个字符串本身长

最后的问题就是如何找到字典树中满足上述所有要求的最深节点。 最有效的方法就是建立一颗包含字符串 \([S_1 \ldots S_n]\) 的字典树。 然后在这颗树中匹配 q 的前缀。 我们从根节点遍历这颗字典树，直到因为不能满足某个条件而不能再遍历为止。

093a52aeacfa1f4b5489bbee3a6d0de22c9dcde6dd72a1c1887f3b75f3eec749-file_1555694178934.png

LeetCode题解

Python版本

自己完成的一个版本，基于垂直扫描思想。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution(object):
    def longestCommonPrefix(self, strs: list) -> str:
            if not len(strs):  # 如果传入的list本身就是空的 直接返回空
                return ""

            min_len = min(len(i) for i in strs)
            _flag = True
            i = 0

            while i < min_len:
                if not _flag:
                    break
                _char = strs[0][i]
                # 一个一个的检查str
                for j in strs:
                    if j[i]!=_char:
                        _flag = False
                        break  # 只要有一个不满足 就不是最大公共前缀了 直接去掉
                
                # 一个一个的检查过后，发现_flag==True，说明没有问题
                if _flag:
                    i += 1

            return '' if i==0 else strs[0][:i]

时间复杂度\(O(n)\)

执行用时 :20 ms, 在所有 Python3 提交中击败了99.88%的用户

内存消耗 :13.2 MB, 在所有 Python3 提交中击败了41.86%的用户

垂直扫描的另一种写法，更加简洁。

1
2
3
4
5
6
7
8
9
10
11
class Solution(object):
    def longestCommonPrefix(self, strs: str) -> str:
        if not len(strs):  # 如果传入的list本身就是空的 直接返回空
            return ""
        for i in range(len(strs[0])):  # 遍历strs[0]的所有字符 比对匹配情况
            c = strs[0][i]  # 取strs[0]当前第i个字符与其他字符串第i个字符对比
            for j in range(len(strs)):
                if i == len(strs[j]) or strs[j][i] != c:  # i == len(strs[j])为遍历完最小字串的情况， strs[j][i] != c为匹配不成功的情况，这两种情况都直接返回现有的匹配结果即可
                    return strs[0][: i]
        
        return strs[0]  # 默认返回第一个字符串

时间复杂度：\(O(S)\)，\(S\) 是所有字符串中字符数量的总和。

空间复杂度：\(O(1)\)，我们只需要使用常数级别的额外空间。

利用Python内建函数set、zip函数实现的垂直扫描。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 复杂版本
class Solution(object):
    def longestCommonPrefix(self, strs: list) -> str:
        # zip(): Return a zip object whose .next() method returns a tuple where the i-th element comes from the i-th iterable argument. The .next() method continues until the shortest iterable in the argument sequence is exhausted and then it raises StopIteration.
        # *strs：先把str list解包为一个个str object
        # zip：再使用zip函数，传入解包之后的一个个str object，将str object中对应的元素打包成一个个元组，然后返回由这些元组组成的对象，
        zip_strs = zip(*strs)
        match_list = []
        for c in zip_strs:
            match_list.append(len(set(c))==1)  # 如果这一个元组只有一个类型的char，说明每个输入str在这个位置的char是一样的。即匹配成功。
        match_list.append(0)  # 留一个0作为定位符
        return strs[0][:match_list.index(0)] if strs else ''  # 取0前面那一位的下标，作为终止位置。

# 2行的简洁版本
class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        r = [len(set(c)) == 1 for c in zip(*strs)] + [0]
        return strs[0][:r.index(0)
                      ] if strs else ''

# 甚至os模块自己就提供最长公共前缀的匹配函数
import os
class Solution:
	def longestCommonPrefix(self, strs: List[str]) -> str:
 		return os.path.commonprefix(strs)

时间复杂度\(O(n)\)

水平扫描

1
2
3
4
5
6
7
8
9
10
11
class Solution(object):
    def longestCommonPrefix(self, strs: list) -> str:
        if not len(strs):  # 如果传入的list本身就是空的 直接返回空
            return ""
        prefix = strs[0]  # 设置第1个字符串为默认最长公共前缀
        for i in range(1, len(strs)):  # 第0个就不用匹配了，从第1个开始一直匹配到第len(strs)个
            while strs[i].find(prefix) != 0:  # 用这句话判断当前prefix是不是也是其他字符串的前缀
                prefix = prefix[:-1]  # 减少前缀
                if not prefix:  # 当 prefix为空时，匹配不成功，直接返回""。
                    return ""
        return prefix

时间复杂度：\(O(S)\)，\(S\) 是所有字符串中字符数量的总和。

空间复杂度：\(O(1)\)，我们只需要使用常数级别的额外空间。

分治算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution(object):
    def longestCommonPrefix(self, strs: str) -> str:
        if len(strs) == 0:  # 如果传入的list本身就是空的 直接返回空
            return ""
        
        return self.divide_rule(strs, 0, len(strs)-1)

    def divide_rule(self, strs, l, r):
        if l == r:
            return strs[l]
        else:
            mid = (l+r)//2  # 注意，这里整除以要用//
            lcpLeft = self.divide_rule(strs, l, mid)
            lcpRight = self.divide_rule(strs, mid+1, r)
            return self.commonPrefix(lcpLeft, lcpRight)
    
    def commonPrefix(self, left, right):
        _min = min(len(left), len(right))
        for i in range(_min):
            if left[i] != right[i]:
                return left[: i]
        return left[: _min]

时间复杂度：\(O(S)\)，\(S\) 是所有字符串中字符数量的总和，\(S=m*n\)。

时间复杂度的递推式为 \(T(n)=2\cdot T(\frac{n}{2})+O(m)\)，化简后可知其就是 \(O(S)\)。最好情况下，算法会进行 \(minLen\cdot n\) 次比较，其中 \(minLen\) 是数组中最短字符串的长度。

空间复杂度：\(O(m \cdot log(n))\)

内存开支主要是递归过程中使用的栈空间所消耗的。 一共会进行 \(log(n)\) 次递归，每次需要 mm 的空间存储返回结果，所以空间复杂度为 \(O(m\cdot log(n))\)。

二分查找算法实现（结合了垂直扫描）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution(object):
    def longestCommonPrefix(self, strs):
        if len(strs) == 0:  # 如果传入的list本身就是空的 直接返回空
            return ""

        minLen = min([len(s) for s in strs])
        low = 0
        high = minLen
        while low <= high:
            middle = (low + high) // 2
            if self.isCommonPrefix(strs, middle):  # 前面是有效的，继续找后面。
                low = middle + 1
            else:  # 前面是无效的，那后面的部分必定也无用缩小前区间的范围，继续往前寻找。
                high = middle - 1 

        return strs[0][: (low + high) // 2]
    
    def isCommonPrefix(self, strs, _len):
        tmp_str = strs[0][: _len]
        for i in range(len(strs)):  # 这里做的是垂直扫描
            if strs[i].find(tmp_str) != 0:
                return False
        return True

最坏情况下，我们有 n 个长度为 m 的相同字符串。

时间复杂度：\(O(S \cdot log(n))\)，其中 \(S\) 所有字符串中字符数量的总和。

算法一共会进行 \(log(n)\) 次迭代，每次一都会进行 \(S = m*n\) 次比较，所以总时间复杂度为 \(O(S \cdot log(n))\)。

空间复杂度：\(O(1)\)，我们只需要使用常数级别的额外空间。

有效语法糖

1、set()函数可以去重

1
2
3
4
5
6
7
8
>>> a = ("1", "1", "2", "2", "3", "3", "4", "4", "5", "5")
>>> a
('1', '1', '2', '2', '3', '3', '4', '4', '5', '5')
>>> b = set(a)
>>> type(b)
<class 'set'>
>>> b
{'3', '5', '4', '2', '1'}

2、zip() 函数用于将可迭代的对象作为参数，将对象中对应的元素打包成一个个元组，然后返回由这些元组组成的对象，这样做的好处是节约了不少的内存。我们可以使用 list() 转换来输出列表。如果各个迭代器的元素个数不一致，则返回列表长度与最短的对象相同，利用 ***** 号操作符，可以将元组解压为列表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
>>> a = [1,2,3]
>>> b = [4,5,6]
>>> c = [4,5,6,7,8]
>>> zipped = zip(a,b)     # 返回一个对象
>>> zipped
<zip object at 0x103abc288>
>>> list(zipped)  # list() 转换为列表
[(1, 4), (2, 5), (3, 6)]
>>> list(zip(a,c))              # 元素个数与最短的列表一致
[(1, 4), (2, 5), (3, 6)]
 
>>> a1, a2 = zip(*zip(a,b))          # 与 zip 相反，zip(*) 可理解为解压，返回二维矩阵式
>>> list(a1)
[1, 2, 3]
>>> list(a2)
[4, 5, 6]
>>>