LeetCode 10. 正则表达式匹配（难）& 面试题19. 正则表达式匹配（难）

从递归回溯到动态规划实现正则匹配

题目

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 . 和 * 的正则表达式匹配。

. 匹配任意单个字符 * 匹配或多个前面的那一个元素 所谓匹配，是要涵盖整个字符串 s 的，而不是部分字符串。

说明: s 可能为空，且只包含从 a-z 的小写字母。 p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。

测试用例

功能测试（模式字符串里包含普通字符、、”*”；模式字符串和输入字符串匹配/不匹配）。 特殊输入测试（输入字符串和模式字符串是nullptr、空字符串）。

考点

考查应聘者对字符串的编程能力。考查应聘者对正则表达式的理解。 考查应聘者思维的全面性。应聘者要全面考虑普通字符、和*并分别分析它们的匹配模式。在应聘者写完代码之后，面试官会要求他/她测试自己的代码。这时候应聘者要充分考虑普通字符、. 和 *三者的排列组合，尽量完备地想出所有可能的测试用例。

示例

示例 1:

1
2
3
4
输入:
s = "aa"
p = "a"
输出: false

解释: "a" 无法匹配 "aa" 整个字符串。

示例 2:

1
2
3
4
输入:
s = "aa"
p = "a*"
输出: true

解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3:

1
2
3
4
输入:
s = "ab"
p = ".*"
输出: true

解释: ".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

示例 4:

1
2
3
4
输入:
s = "aab"
p = "c*a*b"
输出: true

解释: 因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。

示例 5:**

1
2
3
4
5
6
7
输入:
s = "mississippi"
p = "mis*is*p*."
输出: false
s = 'misisisppp'
p = "mis*is*p*."
输出: true

考察知识点

动态规划、回溯算法

核心思想

递归

要实现正则匹配，就要做三件事情： 1、对第一个字符进行匹配：first_match = bool(text) and pattern[0] in {text[0], '.'} 2、当模式中的第二个字符是*时，问题要复杂一些，因为可能有多种不同的匹配方式。一种选择是在字符串不变，模式向后移动两个字符，self.isMatch(text, pattern[2:])。这相当于*和它前面的字符被忽略了，因为*可以匹配字符串中的0个字符。另一种选择是如果模式中的第一个字符和字符串中的第一个字符相匹配，则在字符串上向后移动一个字符，模式保持不变，first_match and self.isMatch(text[1:], pattern)。 3、当模式中的第二个字符不是*时，问题要简单很多。如果字符串中的第一个字符和模式中的第一个字符相匹配，那么在字符串和模式上都向后移动一个字符，然后匹配剩余的字符串和模式。如果字符串中的第一个字符和模式中的第一个字符不相匹配，则直接返回false。return first_match and self.isMatch(text[1:], pattern[1:])

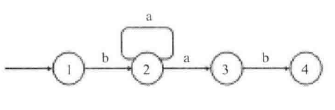
如下图，当匹配进入状态2并且字符串的字符是a时，我们有两种选择，进入状态3（字符串不变，模式向后移动两个字符），也可以保持在状态2不变（字符串向后移动一个字符，模式保持不变）。

Snipaste_2020-05-06_15-53-35.png

动态规划

在递归的代码的基础上，添加mome保存中间结果，自下而上的解决问题。 有的读者也许会问，你怎么知道这个问题是个动态规划问题呢，你怎么知道它就存在「重叠子问题」呢，这似乎不容易看出来呀？ 解答这个问题，最直观的应该是随便假设一个输入，然后画递归树，肯定是可以发现相同节点的。这属于定量分析，其实不用这么麻烦，下面我来教你定性分析，一眼就能看出「重叠子问题」性质。 先拿最简单的斐波那契数列举例，我们抽象出递归算法的框架：

1
2
3
def fib(n):
    fib(n - 1)
    fib(n - 2)

看着这个框架，请问原问题 f(n) ，如何触达子问题 f(n - 2)？有两种路径，一是 f(n) -> f(n-1) -> f(n - 1 - 1), 二是 f(n) -> f(n - 2)。前者经过两次递归，后者进过一次递归而已。两条不同的计算路径都到达了同一个问题，这就是「重叠子问题」，而且可以肯定的是，只要你发现一条重复路径，这样的重复路径一定存在千万条，意味着巨量子问题重叠。 同理，对于本问题，我们依然先抽象出算法框架：

1
2
3
4
def dp(i, j):
    dp(i, j + 2)     #1
    dp(i + 1, j)     #2
    dp(i + 1, j + 1) #3

提出类似的问题，请问如何从原问题 dp(i, j)，触达子问题 dp(i + 2, j + 2)？至少有两种路径，一是 dp(i, j) -> #3 -> #3，二是 dp(i, j) -> #1 -> #2 -> #2。因此，本问题一定存在重叠子问题，一定需要动态规划的优化技巧来处理。

详情可以查看链接，由浅及深，讲述的非常准确。 参考连接

Python版本

  • 递归回溯，暴力破解方法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution(object):
    # 暴力递归
    def isMatch(self, text, pattern):
        if not pattern:  # 当pattern为空时执行以下逻辑
            return not text  # 如果text非空，空pattern无法匹配非空text，应该返回False，而not text就是False。如果txt为空，空pattern可以匹配空text，应该返回True，而 not text就是True。

        first_match = bool(text) and pattern[0] in {text[0], '.'}  # 当前第一个字符是否匹配，考虑了.作为通配符的情况。首先text必须非空所以有bool(text)的条件，其次pattern[0]需要为.或者和text[0]相等。

        # 考虑无限匹配符*的情况
        if len(pattern) >= 2 and pattern[1] == '*':
            res = (
                self.isMatch(text, pattern[2:]) or # 考虑匹配0次（传入self.isMatch的是text和pattern[:2]，代表当前text不匹配且跳过pattern[0]和patter[1]，即跳过*匹配项。）
                (first_match and self.isMatch(text[1:], pattern))  # 或者考虑递归匹配1次，要求first_match为true（传入self.isMatch的是text[1:]和pattern，代表当前text[0]已经算匹配了的，继续考虑*匹配项。这两种考虑是or关系，因为题干里面说了'*'是指匹配零个或多个前面的那一个元素。）
            ) 
            return res
         # 不是无限，匹配符*的情况，简单的把text和pattern都往后调整即可。
        else:
            return first_match and self.isMatch(text[1:], pattern[1:])
  • 动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution(object):
    # 带备忘录的递归
    def isMatch(self, text, pattern) -> bool:
        memo = dict() # 定义全局备忘录
        def dp(i, j):  # i是text的索引 j是pattern的索引
            if (i, j) in memo: return memo[(i, j)]
            if j == len(pattern): return i == len(text)  # 同上，当pattern为空时（j == len(pattern)）直接返回txt是否为空，空pattern和空text，刚好匹配上，返回Ture，否则，空pattern非空text，无法匹配，返回False。

            first = i < len(text) and pattern[j] in {text[i], '.'}  # 同上，i < len(text)代表i未能超出text，而pattern[j] in {text[i], '.'}代表在进行单字符匹配且考虑了.通配符的情况
            
            # 判断是否是*通配符的情况
            if j <= len(pattern) - 2 and pattern[j + 1] == '*':  # 同上，不过是换用了索引表示。 j <= len(pattern) - 2表示patter至少还有两位未匹配。pattern[j + 1] == '*'代表为*通配符的情况
                ans = dp(i, j + 2) or first and dp(i + 1, j)  # 同上，匹配零次，text不动，pattern跳过*通配符的情况（如a*）。或匹配1次，text匹配一个字符（i + 1），pattern不动，保留*通配符的情况（如a*）。
            else:
                ans = first and dp(i + 1, j + 1)  # 非*通配符的情况，text和pattern都完成当前字符匹配，顺次后移（i + 1, j + 1）即可。

            memo[(i, j)] = ans  # 将匹配成功的情况记录在备忘录中
            return ans  # 返回匹配结果
        
        return dp(0, 0)  # 默认text和pattern的索引都从0开始

  • 去注释简洁版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution(object):
    def isMatch(self, text, pattern):
        if not pattern:
            return not text

        first_match = bool(text) and pattern[0] in {text[0], '.'}

        if len(pattern) >= 2 and pattern[1] == '*':
            res = (
                self.isMatch(text, pattern[2:])
                or
                (first_match and self.isMatch(text[1:], pattern))
            )
            return res
        else:
            return first_match and self.isMatch(text[1: ], pattern[1: ])

        
class Solution(object):
    def isMatch(self, text, pattern):
        memo = dict()
        def dp(i, j):
            if (i, j) in memo:  return memo[(i, j)]
            if j == len(pattern):  return i == len(text)
            first_match = i < len(text) and pattern[j] in {text[i], '.'}

            if j <= len(pattern) - 2 and pattern[j + 1] == '*':
                ans = dp(i, j+2) or first_match and dp(i+1, j)
            else:
                ans = first_match and dp(i+1, j+1)
            
            memo[(i, j)] = ans
            return ans
        return dp(0, 0 )