排序算法的C++实现

排序算法千千万万，为什么是你？

比较类排序

通过元素比较来决定相对次序，时间复杂度不能突破 \(O(nlogn)\)，又称非线性时间比较类排序。

交换排序

冒泡排序（Bubble Sort）

算法思想

重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换的元素，也就是说该数列已经排序完成。

  • 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
  • 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
  • 针对所有的元素重复以上的步骤，每次都从第0个元素开始两两交换，第 n 次交换到第 len(nums)-1-n 个元素，0<n<len(nums)-1；
  • 重复步骤1~3，直到排序完成。

图示

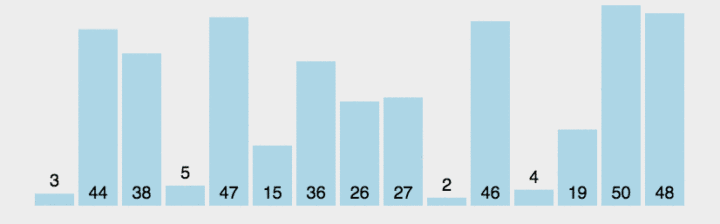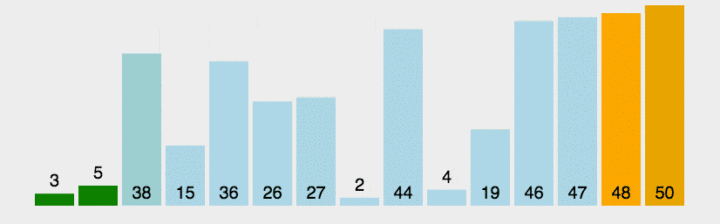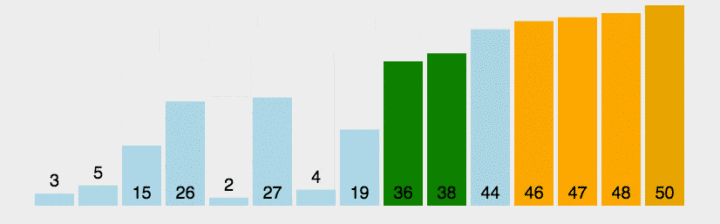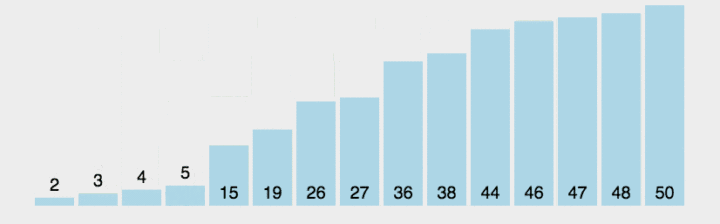
v2-33a947c71ad62b254cab62e5364d2813_b.gif

C++实现

1

时空复杂度和稳定性

稳定性 时间复杂度（平均） 时间复杂度（最坏） 时间复杂度（最好） 空间复杂度
稳定 \(O(n^2)\) \(O(n^2)\) \(O(n)\) \(O(1)\)

快速排序（Quick Sort）

算法思想

基于分治的思想

  • 先从数列中取出一个数作为key值；
  • 将比这个数小的数全部放在它的左边，大于或等于它的数全部放在它的右边；
  • 递归的对左右两个小数列重复第二步，直至各区间只有1个数。

图示

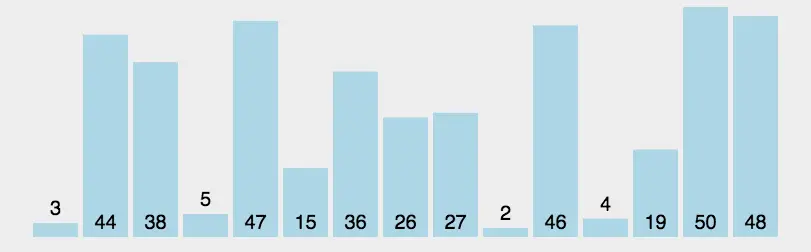
C++实现

1

时空复杂度和稳定性

稳定性 时间复杂度（平均） 时间复杂度（最坏） 时间复杂度（最好） 空间复杂度
不稳定 \(O(nlog_2n)\) \(O(n^2)\) \(O(nlog_2n)\) \(O(nlog_2n)\)

插入排序

简单插入排序（Insertion Sort）

算法思想

将无序部分中的元素插入到有序部分。初始化时，从第一个元素开始，依次搜索每一个元素的待插入位置，算法中，有序部分在前，无序部分在后，一边寻找插入位置，一边将元素后移一个单元。一直在往前找适和当前元素的位置。

图示

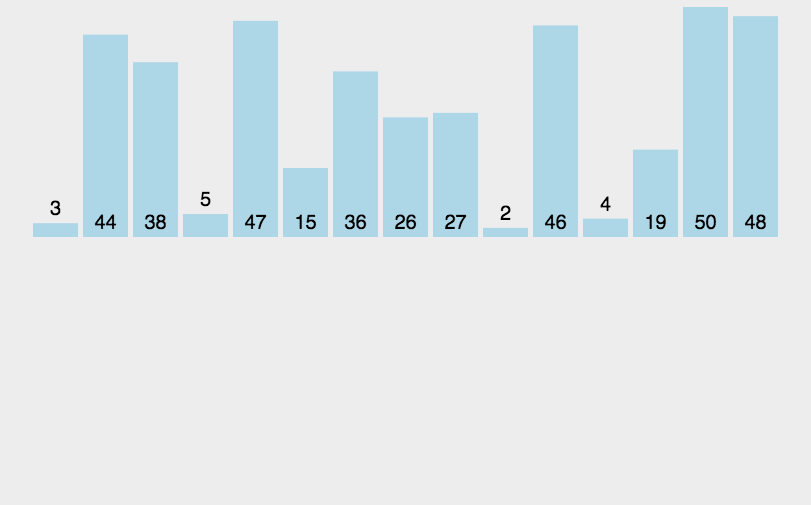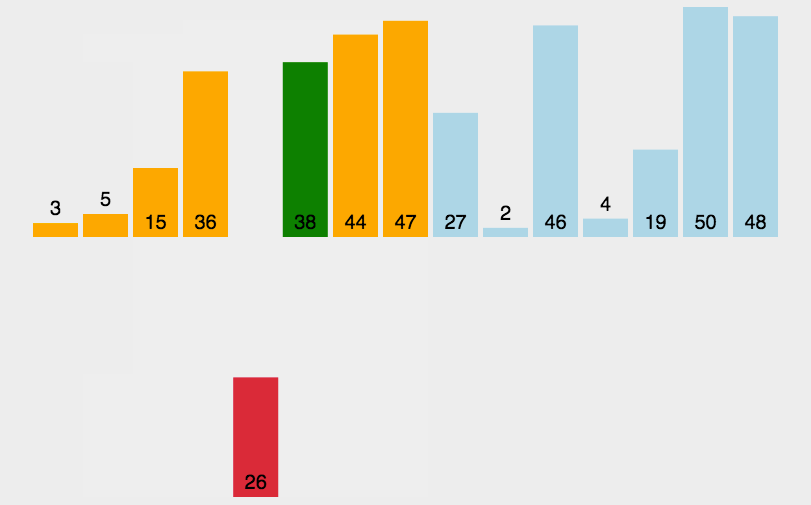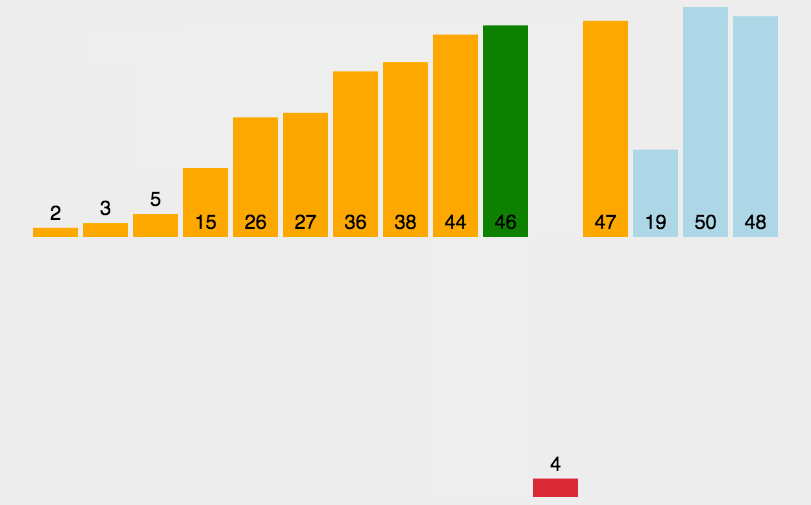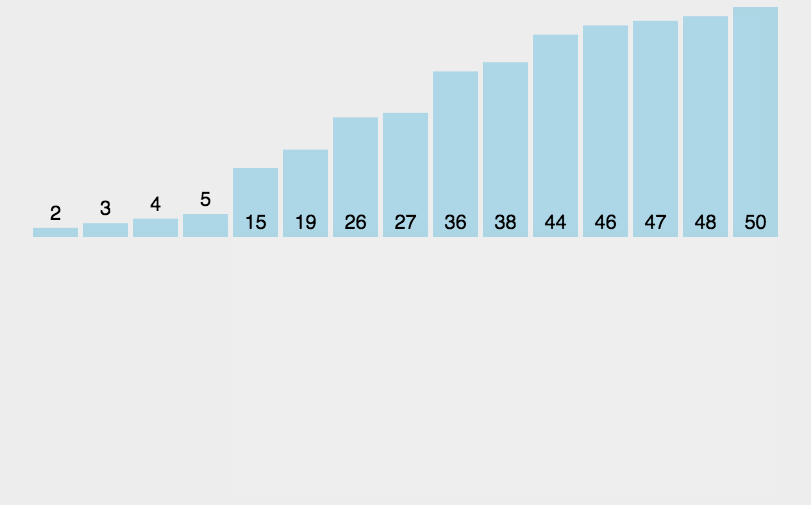
C++实现

1

时空复杂度和稳定性

稳定性 时间复杂度（平均） 时间复杂度（最坏） 时间复杂度（最好） 空间复杂度
稳定 \(O(n^2)\) \(n(n^2)\) \(O(n)\) \(O(1)\)

希尔排序（Shell Sort）

算法思想

简单插入排序的修改版，根据步长由长到短分组，进行排序，直到步长为1为止，属于插入排序的一种。1959年Shell发明，第一个突破 \(O(n^2)\) 的排序算法，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

图示

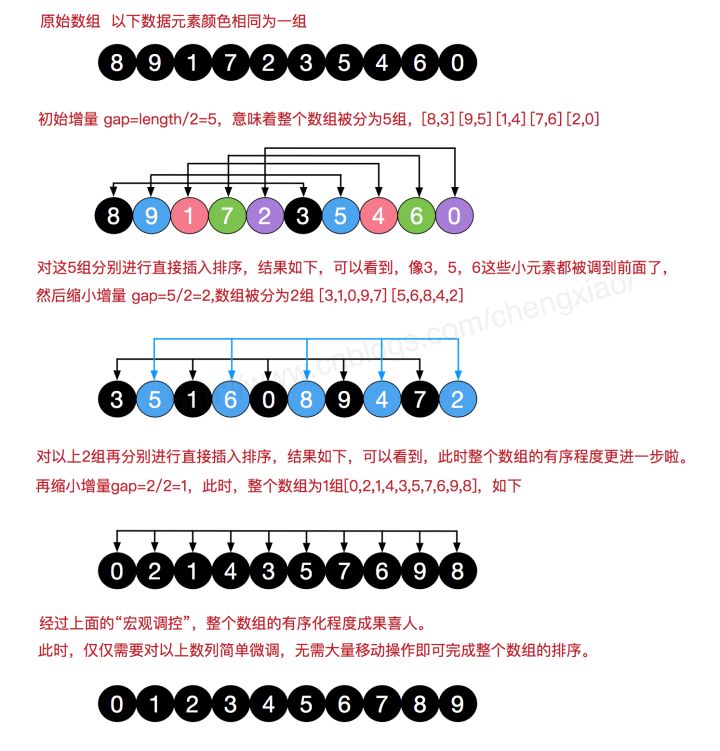
v2-c52e08027910d98f78ee1d225cf03a8b_720w.jpg

C++实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <stdio.h>

void ShellSort(SqList *L){
    int i,j;
    int increment=L->length;
    do{
        // 增量序列
        increment=increment/3+1;
        // 将L->r[i]插入有序增量子表
        for(i=increment+1;i<L->length;i++){
            // 暂存L->[0]
            L->r[0]=L->[i];
            for(j=i-increament; j>0&&L->r[0]<L->r[j]; j-=increment){
                // 记录后移找到插入位置
                L->r[j+increment]=L->r[j];
            // 插入
            L->r[j+increment]=L->r[0];
            }
        }
    }
}

时空复杂度和稳定性

希尔排序的平均时间复杂度和步长序列有之间关系

稳定性 步长序列 时间复杂度（最坏） 时间复杂度（最好） 空间复杂度
不稳定 \(2^i3^j\) \(O(nlog^2n)\) \(O(n)\) \(O(n)\)
\(2^k-1\) \(O(n^{\frac{3}{2}})\) \(O(n)\) \(O(n)\)
\(\frac{n}{2^i}\) \(O(n^2)\) \(O(n)\) \(O(n)\)

选择排序

简单选择排序（Selection Sort）

算法思想

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始（末尾）位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到未排序序列的末尾。以此类推，直到所有元素均排序完毕。注意，这里有个有序区和无序区的概念。

图示

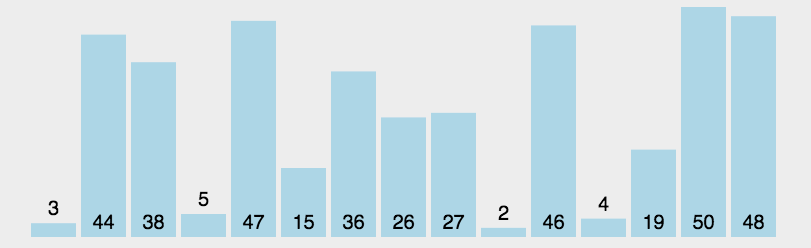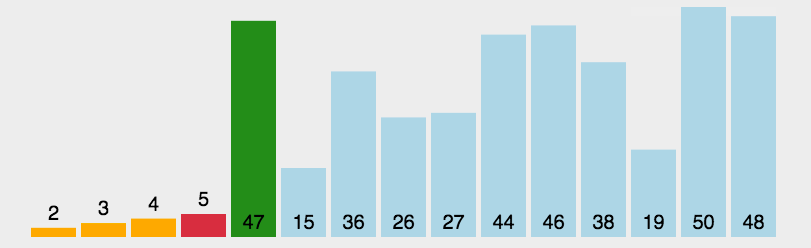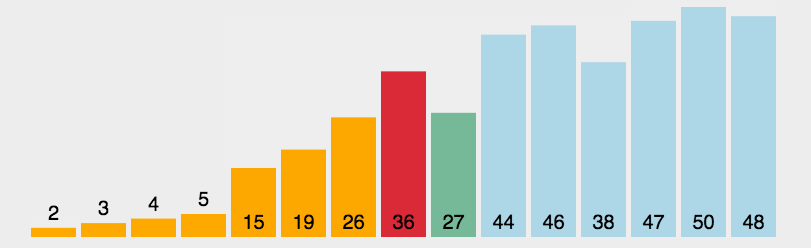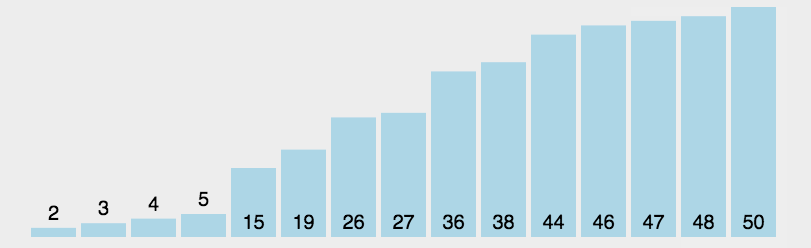
C++实现

1

时空复杂度和稳定性

稳定性 时间复杂度（平均） 时间复杂度（最坏） 时间复杂度（最好） 空间复杂度
不稳定 \(O(n^2)\) \(n(n^2)\) \(O(n^2)\) \(O(1)\)

堆排序（Heap Sort）

算法思想

堆排序是一种基于二叉堆（Binary Heap）结构的排序算法，所谓二叉堆，就是一种特殊的完全二叉树，只不过相比较完全二叉树而言，二叉堆的所有父节点的值都大于（或者小于）它的孩子节点，像这样：

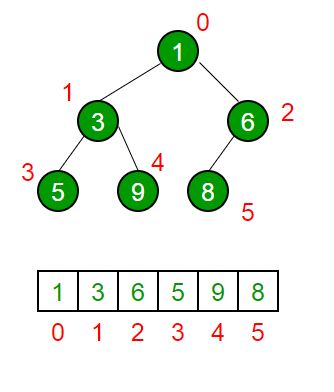
v2-5d6119c9801eadb83402ef68f6d4b689_720w.jpg

首先需要引入最大堆（大根堆）的定义：

  • 最大堆中的最大元素值出现在根结点（堆顶）
  • 堆中每个父节点的元素值都大于等于其孩子结点

类似的，还有最小堆（小根堆）：

  • 最大堆中的最小元素值出现在根结点（堆顶）
  • 堆中每个父节点的元素值都小于等于其孩子结点
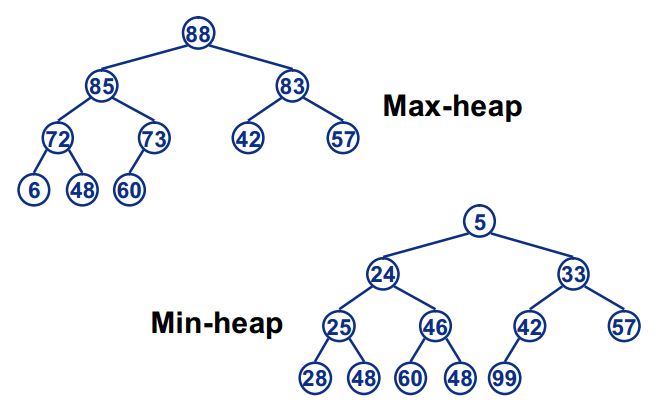
650075-91f1549ff0c87c15.png

那么，堆排序算法的内容就很简单了，最大堆堆顶的最大数取出，将剩余的堆继续调整为最大堆，再次将堆顶的最大数取出，这个过程持续到剩余数只有一个时结束。

图示

C++实现

1

时空复杂度和稳定性

稳定性 时间复杂度（平均） 时间复杂度（最坏） 时间复杂度（最好） 空间复杂度
不稳定 \(O(nlog_2n)\) \(n(nlog_2n)\) \(O(nlog_2n)\) \(O(1)\)

归并排序

二路归并排序（Merge Sort）

算法思想

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）思想。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。若将K个有序表合并成一个有序表，称为多路归并排序。

  • 如果给的数组只有一个元素的话，直接返回（也就是递归到最底层的一个情况）
  • 把整个数组分为尽可能相等的两个部分（分）
  • 对于两个被分开的两个部分进行整个归并排序（治）
  • 把两个被分开且排好序的数组拼接在一起

图示

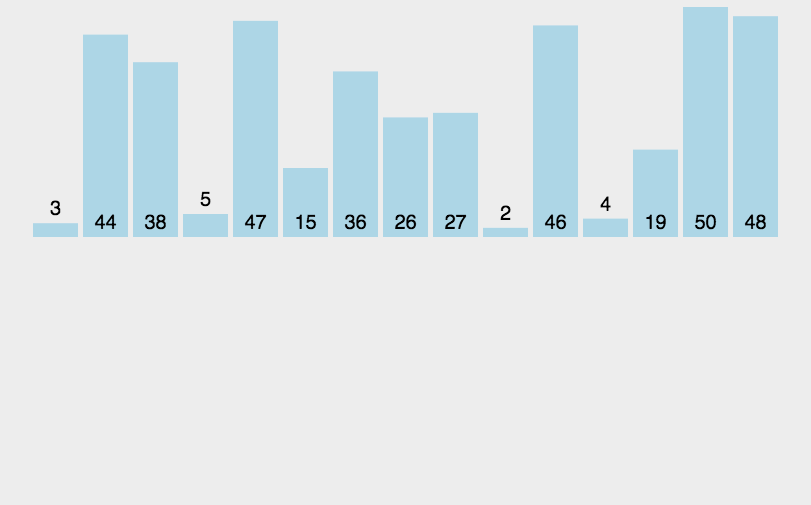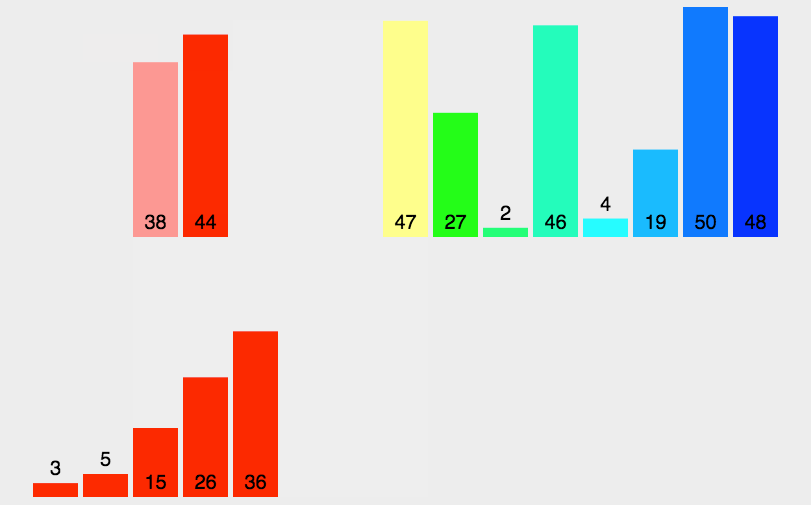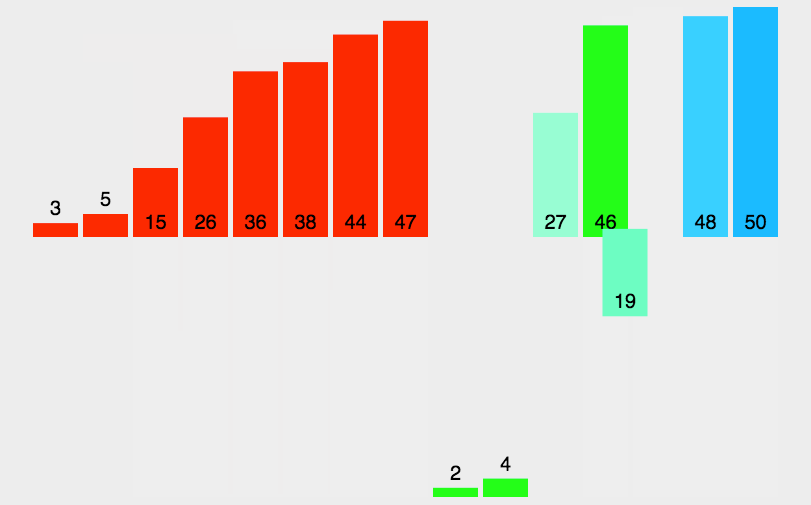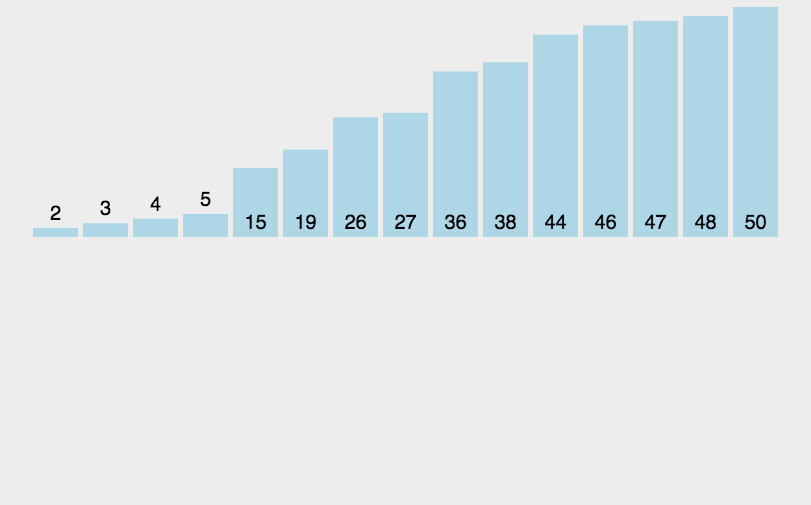
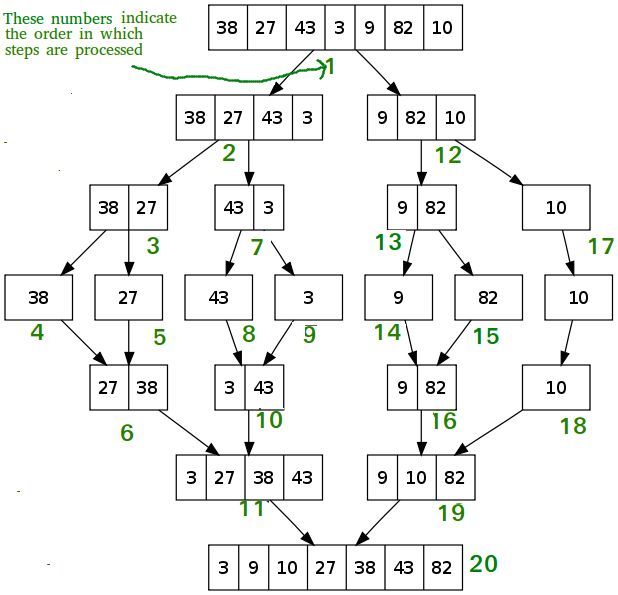
v2-6639ef7ed441b0e2b7a71ee202e3ad05_720w.jpg

C++实现

1

时空复杂度和稳定性

稳定性 时间复杂度（平均） 时间复杂度（最坏） 时间复杂度（最好） 空间复杂度
稳定 \(O(nlog_2n)\) \(O(nlog_2n)\) \(O(nlog_2n)\) \(O(n)\)

非比较类排序

不通过比较来决定元素间的相对次序，时间复杂度可以达到 \(O(n)\)，又称线性时间非比较类排序。

计数排序（Counting Sort）

算法思想

计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。条件苛刻，且牺牲空间换取时间。

图示

C++实现

1

时空复杂度和稳定性

稳定性 时间复杂度（平均） 时间复杂度（最坏） 时间复杂度（最好） 空间复杂度
稳定 \(O(n + k)\) \(O(n + k)\) \(O(n + k)\) \(O(n + k)\)

\(n\) 是待排序元素个数，\(k\) 是待排序元素区间长度。

桶排序（Bucket sort）

算法思想

桶排序是计数排序的升级版，桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。

桶排序过程中存在两个关键环节： 1、元素值域的划分，也就是元素到桶的映射规则。映射规则需要根据待排序集合的元素分布特性进行选择。 2、排序算法的选择，从待排序集合中元素映射到各个桶上的过程，并不存在元素的比较和交换操作，在对各个桶中元素进行排序时，可以自主选择合适的排序算法，桶排序算法的复杂度和稳定性，都根据选择的排序算法不同而不同。

算法过程：

  • 设置一个定量的数组当作空桶；
  • 遍历输入数据，并且把数据一个一个放到对应的桶里去；
  • 对每个不是空的桶进行排序；
  • 从不是空的桶里把排好序的数据拼接起来。

图示

C++实现

1

时空复杂度和稳定性

稳定性 时间复杂度（平均） 时间复杂度（最坏） 时间复杂度（最好） 空间复杂度
稳定 \(O(n+k)\) \(n(n^2)\) \(O(n)\) \(O(n+k)\)

\(n\) 是待排序元素个数，\(k\) 是待排序元素区间长度。

基数排序（Radix Sort）

算法思想

基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。

  • 取得数组中的最大数，并取得位数；
  • nums 为原始数组，从最低位开始取每个位组成 radix 数组；
  • 对 radix 进行计数排序（利用计数排序适用于小范围数的特点）；

图示

C++实现

1

时空复杂度和稳定性

稳定性 时间复杂度（平均） 时间复杂度（最坏） 时间复杂度（最好） 空间复杂度
稳定 \(O(n \times k)\) \(O(n \times k)\) \(O(n \times k)\) \(O(n + k)\)

其中 \(n\) 是排序元素个数，\(k\) 是数字位数。